Straight Lines- 3 NCERT Solutions | Mathematics for NDA PDF Download
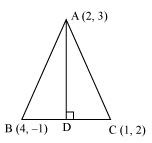
Question 51: In the triangle ABC with vertices A (2, 3), B (4, –1) and C (1, 2), find the equation and length of altitude from the vertex A.
ANSWER : - Let AD be the altitude of triangle ABC from vertex A.
Accordingly, AD⊥BC
The equation of the line passing through point (2, 3) and having a slope of 1 is
(y – 3) = 1(x – 2)
⇒ x – y + 1 = 0
⇒ y – x = 1
Therefore, equation of the altitude from vertex A = y – x = 1.
Length of AD = Length of the perpendicular from A (2, 3) to BC
The equation of BC is
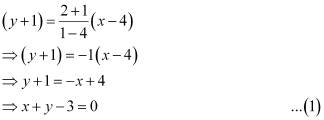
The perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by 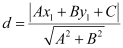 .
.
On comparing equation (1) to the general equation of line Ax + By + C = 0, we obtain A = 1, B = 1, and C = –3.
∴Length of AD 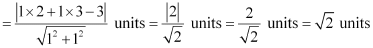
Thus, the equation and the length of the altitude from vertex A are y – x = 1 and 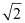 units respectively.
units respectively.
Question 52: If p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that 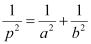 .
.
ANSWER : - It is known that the equation of a line whose intercepts on the axes are a and b is
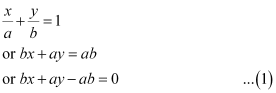
The perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by 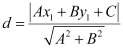 .
.
On comparing equation (1) to the general equation of line Ax + By + C = 0, we obtain A = b, B = a, and C = –ab.
Therefore, if p is the length of the perpendicular from point (x1, y1) = (0, 0) to line (1), we obtain
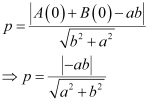
On squaring both sides, we obtain
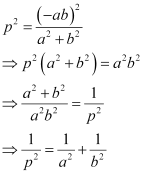
Hence, we showed that 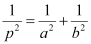 .
.
Question 53: Find the values of k for which the line 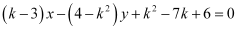 is
is
(a) Parallel to the x-axis,
(b) Parallel to the y-axis,
(c) Passing through the origin.
ANSWER : - The given equation of line is
(k – 3) x – (4 – k2) y + k2 – 7k + 6 = 0 … (1)
(a) If the given line is parallel to the x-axis, then
Slope of the given line = Slope of the x-axis
The given line can be written as
(4 – k2) y = (k – 3) x + k2 – 7k 6 = 0
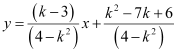 ,
,
which is of the form y = mx + c.
∴Slope of the given line = 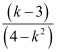
Slope of the x-axis = 0
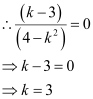
Thus, if the given line is parallel to the x-axis, then the value of k is 3.
(b) If the given line is parallel to the y-axis, it is vertical. Hence, its slope will be undefined.
The slope of the given line is 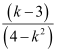 .
.
Now, 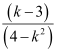 is undefined at k2 = 4
is undefined at k2 = 4
k2 = 4
⇒ k = ±2
Thus, if the given line is parallel to the y-axis, then the value of k is ±2.
(c) If the given line is passing through the origin, then point (0, 0) satisfies the
given equation of line.
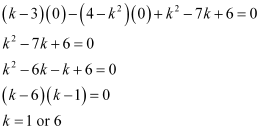
Thus, if the given line is passing through the origin, then the value of k is either 1 or 6.
Question 54: Find the values of θ and p, if the equation 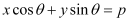 is the normal form of the line
is the normal form of the line 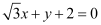 .
.
ANSWER : - The equation of the given line is 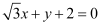 .
.
This equation can be reduced as
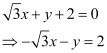
On dividing both sides by 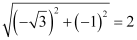 , we obtain
, we obtain
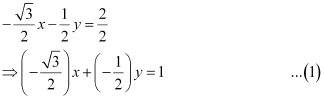
On comparing equation (1) to 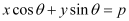 , we obtain
, we obtain
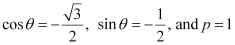
Since the values of sin θ and cos θ are negative, 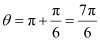
Thus, the respective values of θ and p are 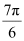 and 1
and 1
Question 55: Find the equations of the lines, which cut-off intercepts on the axes whose sum and product are 1 and –6, respectively.
ANSWER : - Let the intercepts cut by the given lines on the axes be a and b.
It is given that
a + b = 1 … (1)
ab = –6 … (2)
On solving equations (1) and (2), we obtain
a = 3 and b = –2 or a = –2 and b = 3
It is known that the equation of the line whose intercepts on the axes are a and b is
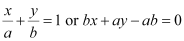
Case I: a = 3 and b = –2
In this case, the equation of the line is –2x + 3y + 6 = 0, i.e., 2x – 3y = 6.
Case II: a = –2 and b = 3
In this case, the equation of the line is 3x – 2y + 6 = 0, i.e., –3x + 2y = 6.
Thus, the required equation of the lines are 2x – 3y = 6 and –3x + 2y = 6.
Question 56: What are the points on the y-axis whose distance from the line 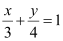 is 4 units.
is 4 units.
ANSWER : - Let (0, b) be the point on the y-axis whose distance from line 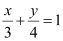 is 4 units.
is 4 units.
The given line can be written as 4x + 3y – 12 = 0 … (1)
On comparing equation (1) to the general equation of line Ax + By + C = 0, we obtain A = 4, B = 3, and C = –12.
It is known that the perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by 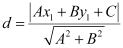 .
.
Therefore, if (0, b) is the point on the y-axis whose distance from line 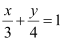 is 4 units, then:
is 4 units, then:
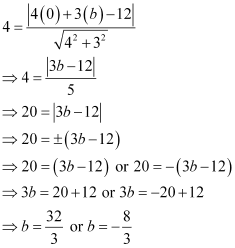
Thus, the required points are 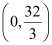 and
and 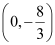 .
.
Question 57: Find the perpendicular distance from the origin to the line joining the points 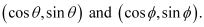
ANSWER : - The equation of the line joining the points 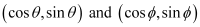 is given by
is given by
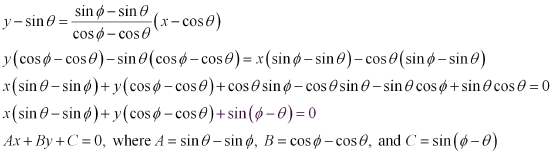
It is known that the perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by 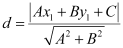 .
.
Therefore, the perpendicular distance (d) of the given line from point (x1, y1) = (0, 0) is

Question 58: Find the equation of the line parallel to y-axis and drawn through the point of intersection of the lines x – 7y + 5 = 0 and 3x + y = 0.
ANSWER : - The equation of any line parallel to the y-axis is of the form
x = a … (1)
The two given lines are
x – 7y + 5 = 0 … (2)
3x + y = 0 … (3)
On solving equations (2) and (3), we obtain 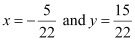 .
.
Therefore, 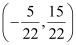 is the point of intersection of lines (2) and (3).
is the point of intersection of lines (2) and (3).
Since line x = a passes through point 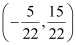 ,
, 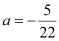 .
.
Thus, the required equation of the line is 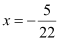 .
.
Question 59: Find the equation of a line drawn perpendicular to the line 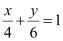 through the point, where it meets the y-axis.
through the point, where it meets the y-axis.
ANSWER : - The equation of the given line is 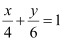 .
.
This equation can also be written as 3x + 2y – 12 = 0
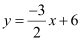 , which is of the form y = mx + c
, which is of the form y = mx + c
∴Slope of the given line 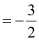
∴Slope of line perpendicular to the given line 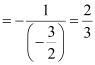
Let the given line intersect the y-axis at (0, y).
On substituting x with 0 in the equation of the given line, we obtain 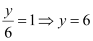
∴The given line intersects the y-axis at (0, 6).
The equation of the line that has a slope of 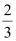 and passes through point (0, 6) is
and passes through point (0, 6) is
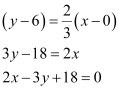
Thus, the required equation of the line is 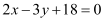 .
.
Question 60: Find the area of the triangle formed by the lines y – x = 0, x + y = 0 and x – k = 0.
ANSWER : - The equations of the given lines are
y – x = 0 … (1)
x + y = 0 … (2)
x – k = 0 … (3)
The point of intersection of lines (1) and (2) is given by
x = 0 and y = 0
The point of intersection of lines (2) and (3) is given by
x = k and y = –k
The point of intersection of lines (3) and (1) is given by
x = k and y = k
Thus, the vertices of the triangle formed by the three given lines are (0, 0), (k, –k), and (k, k).
We know that the area of a triangle whose vertices are (x1, y1), (x2, y2), and (x3, y3) is 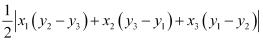 .
.
Therefore, area of the triangle formed by the three given lines
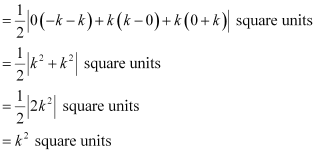
Question 61: Find the value of p so that the three lines 3x + y – 2 = 0, px + 2y – 3 = 0 and 2x – y – 3 = 0 may intersect at one point.
ANSWER : - The equations of the given lines are
3x + y – 2 = 0 … (1)
px + 2y – 3 = 0 … (2)
2x – y – 3 = 0 … (3)
On solving equations (1) and (3), we obtain
x = 1 and y = –1
Since these three lines may intersect at one point, the point of intersection of lines (1) and (3) will also satisfy line (2).
p (1) + 2 (–1) – 3 = 0
p – 2 – 3 = 0
p = 5
Thus, the required value of p is 5.
Question 62: If three lines whose equations are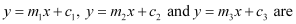 concurrent, then show that
concurrent, then show that 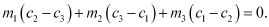
ANSWER : - The equations of the given lines are
y = m1x + c1 … (1)
y = m2x + c2 … (2)
y = m3x + c3 … (3)
On subtracting equation (1) from (2), we obtain
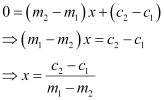
On substituting this value of x in (1), we obtain
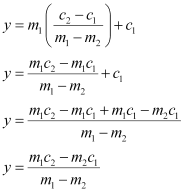
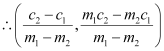 is the point of intersection of lines (1) and (2).
is the point of intersection of lines (1) and (2).
It is given that lines (1), (2), and (3) are concurrent. Hence, the point of intersection of lines (1) and (2) will also satisfy equation (3).
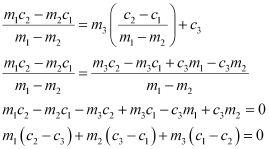
Hence, 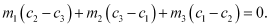
Question 63: Find the equation of the lines through the point (3, 2) which make an angle of 45° with the line x –2y = 3.
ANSWER : - Let the slope of the required line be m1.
The given line can be written as 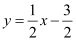 , which is of the form y = mx + c
, which is of the form y = mx + c
∴Slope of the given line = 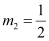
It is given that the angle between the required line and line x – 2y = 3 is 45°.
We know that if θ is the acute angle between lines l1 and l2 with slopes m1 and m2 respectively, then 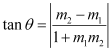 .
.

Case I: m1 = 3
The equation of the line passing through (3, 2) and having a slope of 3 is:
y – 2 = 3 (x – 3)
y – 2 = 3x – 9
3x – y = 7
Case II: m1 = 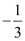
The equation of the line passing through (3, 2) and having a slope of 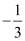 is:
is:
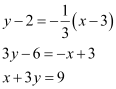
Thus, the equations of the lines are 3x – y = 7 and x + 3y = 9.
Question 64: Find the equation of the line passing through the point of intersection of the lines 4x + 7y – 3 = 0 and 2x – 3y + 1 = 0 that has equal intercepts on the axes.
ANSWER : - Let the equation of the line having equal intercepts on the axes be
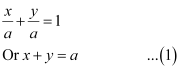
On solving equations 4x + 7y – 3 = 0 and 2x – 3y + 1 = 0, we obtain 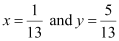 .
.
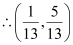 is the point of intersection of the two given lines.
is the point of intersection of the two given lines.
Since equation (1) passes through point 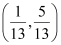 ,
,
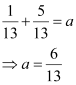
∴ Equation (1) becomes 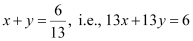
Thus, the required equation of the line is 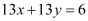 .
.
Question 65: Show that the equation of the line passing through the origin and making an angle θ with the line 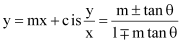 .
.
ANSWER : - Let the equation of the line passing through the origin be y = m1x.
If this line makes an angle of θ with line y = mx + c, then angle θ is given by
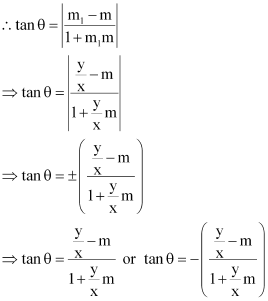
Case I: 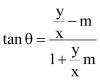
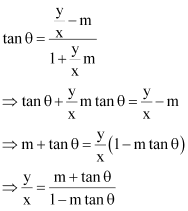
Case II: 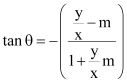
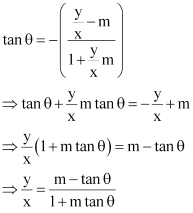
Therefore, the required line is given by 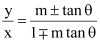 .
.
Question 66: In what ratio, the line joining (–1, 1) and (5, 7) is divided by the line x + y = 4?
ANSWER : - The equation of the line joining the points (–1, 1) and (5, 7) is given by
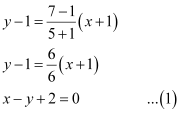
The equation of the given line is
x + y – 4 = 0 … (2)
The point of intersection of lines (1) and (2) is given by
x = 1 and y = 3
Let point (1, 3) divide the line segment joining (–1, 1) and (5, 7) in the ratio 1:k. Accordingly, by section formula,
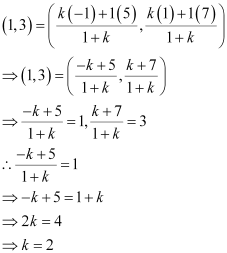
Thus, the line joining the points (–1, 1) and (5, 7) is divided by line
x + y = 4 in the ratio 1:2.
Question 67: Find the distance of the line 4x + 7y + 5 = 0 from the point (1, 2) along the line 2x – y= 0.
ANSWER : - The given lines are
2x – y = 0 … (1)
4x + 7y + 5 = 0 … (2)
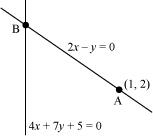
A (1, 2) is a point on line (1).
Let B be the point of intersection of lines (1) and (2).
On solving equations (1) and (2), we obtain 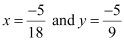 .
.
∴Coordinates of point B are 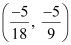 .
.
By using distance formula, the distance between points A and B can be obtained as
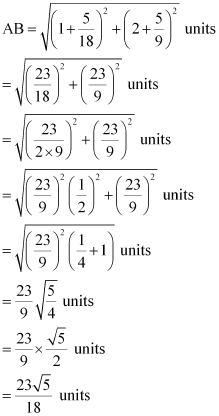
Thus, the required distance is 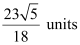 .
.
Question 68: Find the direction in which a straight line must be drawn through the point (–1, 2) so that its point of intersection with the line x y = 4 may be at a distance of 3 units from this point.
ANSWER : - Let y = mx + c be the line through point (–1, 2).
Accordingly, 2 = m (–1) + c.
⇒ 2 = –m + c
⇒ c = m + 2
∴ y = mx + m + 2 … (1)
The given line is
x + y = 4 … (2)
On solving equations (1) and (2), we obtain
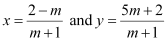
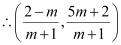 is the point of intersection of lines (1) and (2).
is the point of intersection of lines (1) and (2).
Since this point is at a distance of 3 units from point (– 1, 2), according to distance formula,
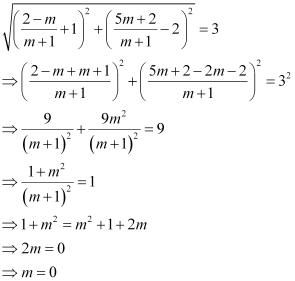
Thus, the slope of the required line must be zero i.e., the line must be parallel to the x-axis.
Question 69: Find the image of the point (3, 8) with respect to the line x +3y = 7 assuming the line to be a plane mirror.
ANSWER : - The equation of the given line is
x + 3y = 7 … (1)
Let point B (a, b) be the image of point A (3, 8).
Accordingly, line (1) is the perpendicular bisector of AB.

Since line (1) is perpendicular to AB,
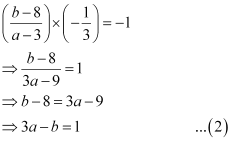
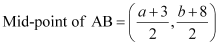
The mid-point of line segment AB will also satisfy line (1).
Hence, from equation (1), we have
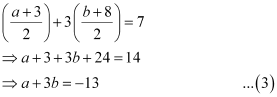
On solving equations (2) and (3), we obtain a = –1 and b = –4.
Thus, the image of the given point with respect to the given line is (–1, –4).
Question 70: If the lines y = 3x + 1 and 2y = x + 3 are equally inclined to the line y = mx + 4, find the value of m.
ANSWER : - The equations of the given lines are
y = 3x + 1 … (1)
2y = x + 3 … (2)
y = mx + 4 … (3)
Slope of line (1), m1 = 3
Slope of line (2), 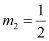
Slope of line (3), m3 = m
It is given that lines (1) and (2) are equally inclined to line (3). This means that
the angle between lines (1) and (3) equals the angle between lines (2) and (3).
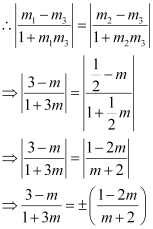

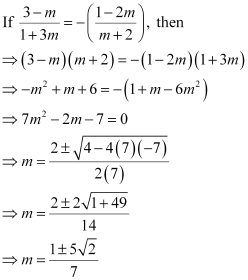
Thus, the required value of m is 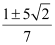 .
.
Question 71: If sum of the perpendicular distances of a variable point P (x, y) from the lines x + y – 5 = 0 and 3x – 2y + 7 = 0 is always 10. Show that P must move on a line.
ANSWER : - The equations of the given lines are
x + y – 5 = 0 … (1)
3x – 2y + 7 = 0 … (2)
The perpendicular distances of P (x, y) from lines (1) and (2) are respectively given by
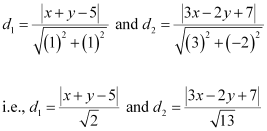
It is given that 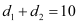 .
.
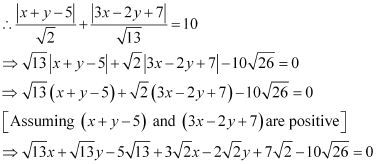
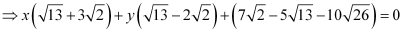 , which is the equation of a line.
, which is the equation of a line.
Similarly, we can obtain the equation of line for any signs of 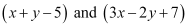 .
.
Thus, point P must move on a line.
Question 72: Find equation of the line which is equidistant from parallel lines 9x + 6y – 7 = 0 and 3x + 2y + 6 = 0.
ANSWER : - The equations of the given lines are
9x + 6y – 7 = 0 … (1)
3x + 2y + 6 = 0 … (2)
Let P (h, k) be the arbitrary point that is equidistant from lines (1) and (2). The perpendicular distance of P (h, k) from line (1) is given by
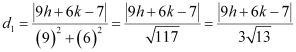
The perpendicular distance of P (h, k) from line (2) is given by
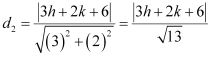
Since P (h, k) is equidistant from lines (1) and (2), 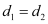
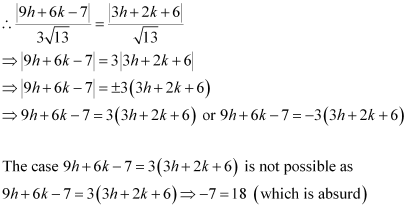
∴ 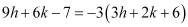
9h + 6k – 7 = – 9h – 6k – 18
⇒ 18h + 12k + 11 = 0
Thus, the required equation of the line is 18x + 12y + 11 = 0.
Question 73: A ray of light passing through the point (1, 2) reflects on the x-axis at point A and the reflected ray passes through the point (5, 3). Find the coordinates of A.
ANSWER : - Let the coordinates of point A be (a, 0).
Draw a line (AL) perpendicular to the x-axis.
We know that angle of incidence is equal to angle of reflection. Hence, let
∠BAL = ∠CAL = Φ
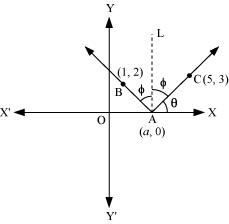
Let ∠CAX = θ
∴∠OAB = 180° – (θ + 2Φ) = 180° – [θ + 2(90° – θ)]
= 180° – θ – 180°+ 2θ
= θ
∴∠BAX = 180° – θ
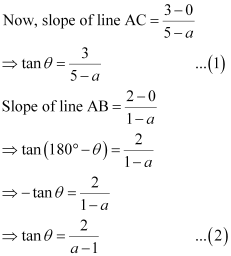
From equations (1) and (2), we obtain
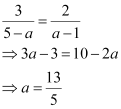
Thus, the coordinates of point A are 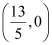 .
.
Question 74: Prove that the product of the lengths of the perpendiculars drawn from the points 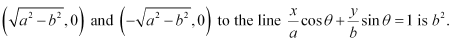
ANSWER : - The equation of the given line is
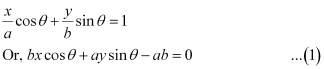
Length of the perpendicular from point 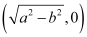 to line (1) is
to line (1) is
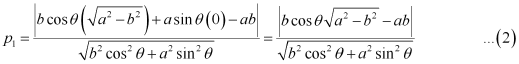
Length of the perpendicular from point 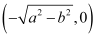 to line (2) is
to line (2) is
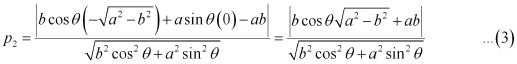
On multiplying equations (2) and (3), we obtain

Hence, proved.
Question 75: A person standing at the junction (crossing) of two straight paths represented by the equations 2x – 3y + 4 = 0 and 3x + 4y – 5 = 0 wants to reach the path whose equation is 6x – 7y + 8 = 0 in the least time. Find equation of the path that he should follow.
ANSWER : - The equations of the given lines are
2x – 3y + 4 = 0 … (1)
3x + 4y – 5 = 0 … (2)
6x – 7y + 8 = 0 … (3)
The person is standing at the junction of the paths represented by lines (1) and (2).
On solving equations (1) and (2), we obtain 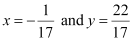 .
.
Thus, the person is standing at point 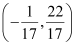 .
.
The person can reach path (3) in the least time if he walks along the perpendicular line to (3) from point 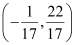 .
.

∴Slope of the line perpendicular to line (3) 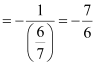
The equation of the line passing through 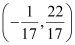 and having a slope of
and having a slope of 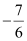 is given by
is given by
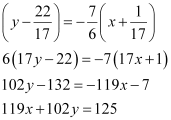
Hence, the path that the person should follow is 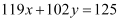 .
.
|
277 videos|265 docs|221 tests
|
FAQs on Straight Lines- 3 NCERT Solutions - Mathematics for NDA
| 1. What are the important concepts and formulas related to straight lines? |  |
| 2. How do you find the equation of a straight line passing through two given points? |  |
| 3. How can we determine the slope of a straight line using its equation? |  |
| 4. What is the significance of the intercepts in a straight line? |  |
| 5. How can we determine the distance between a point and a straight line? |  |

|
Explore Courses for NDA exam
|

|


















