Irodov Solutions: Phase Transformations | Physics Class 11 - NEET PDF Download
Q. 185. A saturated water vapour is contained in a cylindrical vessel under a weightless piston at a temperature t = 100°C. As a result of a slow introduction of the piston a small fraction of the vapour Δm = 0.70 g gets condensed. What amount of work was performed over the gas? The vapour is assumed to be ideal, the volume of the liquid is to be neglected.
Solution. 185. The condensation takes place at constant pressure and temperature and the work done is
p Δ V
where ΔV is the volume of the condensed vapour in the vapour phase. It is
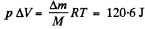
where M = 18 gm is the molecular weight of water.
Q. 186. A vessel of volume V = 6.0 l contains water together with its saturated vapour under a pressure of 40 atm and at a temperature of 250°C. The specific volume of the vapour is equal to V'c = 50 l/kg under these conditions. The total mass of the system water-vapour equals m = 5.0 kg. Find the mass and the volume of the vapour.
Solution. 186. The specific volume of water (the liquid) will be written as 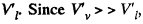 most of the weight is due to water. Thus if ml is mass of the liquid and mv that of the vapour then
most of the weight is due to water. Thus if ml is mass of the liquid and mv that of the vapour then
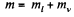
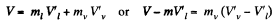
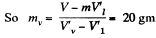 in the present case. Its volume is
in the present case. Its volume is 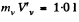
Q. 187. The saturated water vapour is enclosed in a cylinder under a piston and occupies a volume V0 = 5.0 l at the temperature t = 100°C. Find the mass of the liquid phase formed after the volume under the piston decreased isothermally to V = 1.6 l. The saturated vapour is assumed to be ideal.
Solution. 187. The volume of the condensed vapour was originally V0 - V at temperature T = 373 K. Its mass will be given by
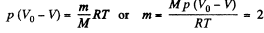 gm where p = atmospheric pressure
gm where p = atmospheric pressure
Q. 188. A volume occupied by a saturated vapour is reduced isothermally n-fold. Find what fraction ri of the final volume is occupied by the liquid phase if the specific volumes of the saturated vapour and the liquid phase differ by N times (N > n). Solve the same problem under the condition that the final volume of the substance corresponds to the midpoint of a horizontal portion of the isothermal line in the diagram p, V.
Solution. 188. 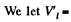 specific volume of liquid.
specific volume of liquid. 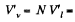 specific volume of vapour.
specific volume of vapour.
Let V = Original volume of the vapour. Then

So 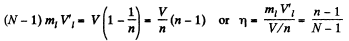
In the case when the final volume of the substance corresponds to the midpoint of a horizontal portion of the isothermal line in the p y v diagram, the final volume must be 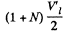 per unit mass of the substance. Of this the volume of the liquid is V'1/2 per unit total mass of the substance.
per unit mass of the substance. Of this the volume of the liquid is V'1/2 per unit total mass of the substance.
Thus 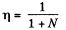
Q. 189. An amount of water of mass m = 1.00 kg, boiling at standard atmospheric pressure, turns completely into saturated vapour. Assuming the saturated vapour to be an ideal gas find the increment of entropy and internal energy of the system.
Solution. 189. From the first law of thermodynamics
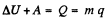
where q is the specific latent heat of vaporization
Now 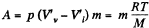
Thus 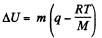
For water this gives 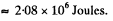
Q. 190. Water of mass m = 20 g is enclosed in a thermally insulated cylinder at the temperature of 0°C under a weightless piston whose area is S = 410 cm2. The outside pressure is equal to standard atmospheric pressure. To what height will the piston rise when the water absorbs Q = 20.0 kJ of heat?
Solution. 190. Some of the heat used in heating water to the boiling temperature
T = 100°C = 373 K The remaining heat
= Q - mc Δ T
(c = specific heat of water, ΔT - 100 K) is used to create vapour. If the piston rises to a height h then the volume of vapour will be ≈ sh(neglecting water). Its mass will be 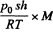 and heat of vapourization will be
and heat of vapourization will be 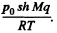 To this must be added the work done in creating the saturated vapour
To this must be added the work done in creating the saturated vapour 
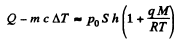
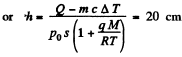
Q. 191. One gram of saturated water vapour is enclosed in a thermally insulated cylinder under a weightless piston. The outside pressure being standard, m = 1.0 g of water is introduced into the cylinder at a temperature t0 = 22°C. Neglecting the heat capacity of the cylinder and the friction of the piston against the cylinder's walls, find the work performed by the force of the atmospheric pressure during the lowering of the piston.
Solution. 191. A quantity 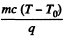 of saturated vapour must condense to heat the w ater to boiling point T = 373°K
of saturated vapour must condense to heat the w ater to boiling point T = 373°K
(Here c = specific heat of water, T0 = 295 K = initial water temperature).
The work done in lowering the piston will then be
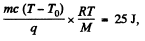
since work done per unit mass o f the condensed vapour is 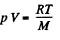
Q. 192. If an additional pressure Δp of a saturated vapour over a convex spherical surface of a liquid is considerably less than the vapour pressure over a plane surface, then 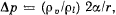 where p0 and Pl are the densities of the vapour and the liquid, α is the surface tension, and r is the radius of curvature of the surface. Using this formula, find the diameter of water droplets at which the saturated vapour pressure exceeds the vapour pressure over the plane surface by η = 1.0% at a temperature t = 27°C. The vapour is assumed to be an ideal gas.
where p0 and Pl are the densities of the vapour and the liquid, α is the surface tension, and r is the radius of curvature of the surface. Using this formula, find the diameter of water droplets at which the saturated vapour pressure exceeds the vapour pressure over the plane surface by η = 1.0% at a temperature t = 27°C. The vapour is assumed to be an ideal gas.
Solution. 192. Given 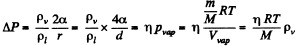
or 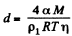
F or water a = 73 dynes/cm, M = 18gm, pl = gm/cc, T = 300 K, and with η = 0.01, we get
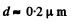
Q. 193. Find the mass of all molecules leaving one square centimetre of water surface per second into a saturated water vapour above it at a temperature t = 100°C. It is assumed that η = 3.6% of all water vapour molecules falling on the water surface are retained in the liquid phase.
Solution. 193. In equilibrium the number of "liquid" molecules evaporoting must equals the number of "vapour" molecules condensing. By kinetic theory, this number is
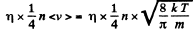
Its mass is
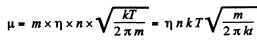
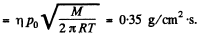
where p0 is atmospheric pressure and T = 373 K and M = molecular weight of water.
Q. 194. Find the pressure of saturated tungsten vapour at a temperature T = 2000 K if a tungsten filament is known to lose a mass μ = 1.2-10-13 g/(s•cm2) from a unit area per unit time when evaporating into high vacuum at this temperature.
Solution. 194. Here we must assume that |i is also the rate at which the tungsten filament loses mass when in an atmosphere of its own vapour at this temperature and that η (of the previous problem) ≈ 1. Then
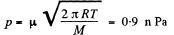
from the previous problem where p = pressure of the saturated vapour.
Q. 195. By what magnitude would the pressure exerted by water on the walls of the vessel have increased if the intermolecular attraction forces had vanished?
Solution. 195. From the Vander Waals equation
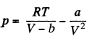
where V = Volume of one gm mole of the substances.
For water V = 18 c.c. per mole = 1*8 x 10-2 itre per mole

If molecular attraction vanished the equation will be
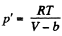
for the same specific volume. Thus
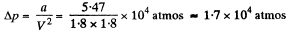
Q. 196. Find the internal pressure pi of a liquid if its density p and specific latent heat of vaporization q are known. The heat q is assumed to be equal to the work performed against the forces of the internal pressure, and the liquid obeys the Van der Waals equation. Calculate pi in water.
Solution. 196. The internal pressure being 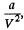 the work done in condensation is
the work done in condensation is
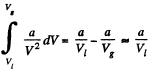
This by assumption is Mq , M being the molecular weight and Vl , Vg being the molar volumes of the liquid and gas.
Thus 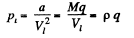
where p is the density of the liquid. For water pi = 3-3 x 1013 atm
Q. 197. Demonstrate that Eqs. (2.6a) and (2.6b) are valid for a substance, obeying the Van der Waals equation, in critical state.
Instruction. Make use of the fact that the critical state corresponds to the point of inflection in the isothermal curve p (V).
Solution. 197. The Vandar Waal's equation can be written as (for one mole)
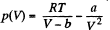
A t the critical point 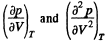 vanish. Thus
vanish. Thus
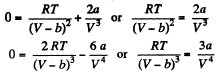
Solving these simultaneously we get on division
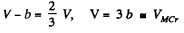
This is the critical molar volume. Putting this back
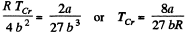
Finally 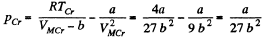
From these we see that 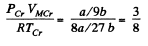
Q. 198. Calculate the Van der Waals constants for carbon dioxide if its critical temperature Tcr = 304 K and critical pressure pcr = 73 atm.
Solution. 198. 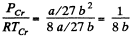
Thus 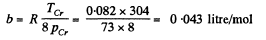
and 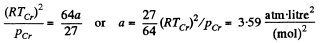
Q. 199. Find the specific volume of benzene (C6H6) in critical state if its critical temperature Tcr = 562 K and critical pressure pcr = 47 atm.
Solution. 199. Specific volume is molar volume divided by molecular weight. Thus
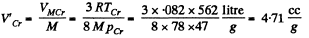
Q. 200. Write the Van der Waals equation via the reduced parameters π, v, and τ, having taken the corresponding critical values for the units of pressure, volume, and temperature. Using the equation obtained, find how many times the gas temperature exceeds its critical temperature if the gas pressure is 12 times as high as critical pressure, and the volume of gas is equal to half the critical volume.
Solution. 200.
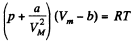
or 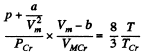
or 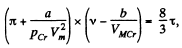
where 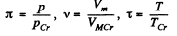
or 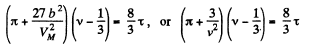
When 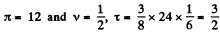
Q. 201. Knowing the Van der Waals constants, find:
(a) the maximum volume which water of mass m = 1.00 kg can occupy in liquid state;
(b) the maximum pressure of the saturated water vapour.
Solution. 201. (a) The ciritical Volume VMCr is the maximum volume in the liquid phase and the minimum volume in the gaseous. Thus
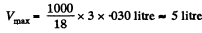
(b) The critical pressure is the maximum possible pressure in the vapour phase in equilibrium with liquid phase. Thus
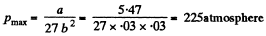
Q. 202. Calculate the temperature and density of carbon dioxide in critical state, assuming the gas to be a Van der Waals one.
Solution. 202.
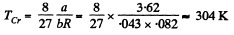
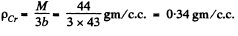
Q. 203. What fraction of the volume of a vessel must liquid ether occupy at room temperature in order to pass into critical state when critical temperature is reached? Ether has Tcr = 467 K, pcr =3 5.5 atm, M = 74 g/mol.
Solution. 203. The vessel is such that either vapour or liquid of mass m occupies it at critical point. Then its volume will be
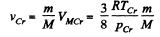
The corresponding volume in liquid phase at room temperature is

where p = density of liquid ether at room tmeperature. Thus
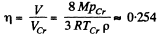
using the given data (and p = 720gm per litre)
Q. 204. Demonstrate that the straight line 1-5 corresponding to the isothermal-isobaric phase transition cuts the Van der Waals isotherm so that areas I and II are equal (Fig. 2.5).
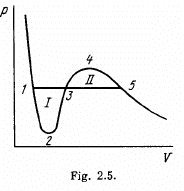
Solution. 204. We apply the relation (T = constant)
This implies that the areas I and II are equal.
This reasoning is inapplicable to the cycle 1231, for example. This cycle is irreversible because it involves the irreversible transition from a single phase to a two-phase state at the point 3.
Q. 205. What fraction of water supercooled down to the temperature t = —20°C under standard pressure turns into ice when the system passes into the equilibrium state? At what temperature of the supercooled water does it turn into ice completely?
Solution. 205. When a portion of supercool water turns into ice some heat is liberated, which should heat it upto ice point. Neglecting the variation of specific heat of water, the fraction of water turning inot ice is clearly

where c = specific heat of water and q ≈ latent heat of fusion of ice, Clearly f = 1 at t = -80°C
Q. 206. Find the increment of the ice melting temperature in the vicinity of 0°C when the pressure is increased by Δp = 1.00 atm. The specific volume of ice exceeds that of water by' ΔV' = 0.091 cm3/g.
Solution. 206. From the Claussius-Clapeyron (C-C)equations
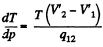
q12 is the specific latent heat absorbed in 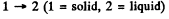
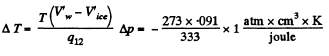

Q. 207. Find the specific volume of saturated water vapour under standard pressure if a decrease of pressure by Ap = 3.2 kPa is known to decrease the water boiling temperature by ΔT = 0.9 K.
Solution. 207. Here 1 = liquid, 2 = Steam
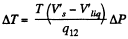
or 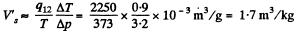
Q. 208. Assuming the saturated water vapour to be ideal, find its pressure at the temperature 101.1 °C.
Solution. 208. From C-C equations
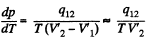
Assuming the saturated vapour to be ideal gas
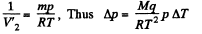
and 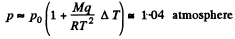
Q. 209. A small amount of water and its saturated vapour are enclosed in a vessel at a temperature t = 100°C. How much (in per cent) will the mass of the saturated vapour increase if the temperature of the system goes up by ΔT = 1.5 K? Assume that the vapour is an ideal gas and the specific volume of water is negligible as compared to that of vapour.
Solution. 209. From C-C equation, neglecting the voolume of the liquid
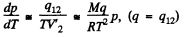
or 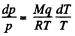
Now 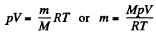 for a perfect gas
for a perfect gas
So 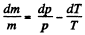 (V is Const = specific volume)
(V is Const = specific volume)
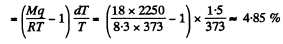
Q. 210. Find the pressure of saturated vapour as a function of temperature p (T) if at a temperature T0 its pressure equals p0. Assume that: the specific latent heat of vaporization q is independent of T, the specific volume of liquid is negligible as compared to that of vapour, saturated vapour obeys the equation of state for an ideal gas. Investigate under what conditions these assumptions are permissible.
Solution. 210. From C-C equation
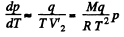
Integrating In p = constant 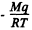
So 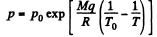
This is reasonable for 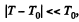 and far below critical temperature.
and far below critical temperature.
Q. 211. An ice which was initially under standard conditions was compressed up to the pressure p = 640 atm. Assuming the lowering of the ice melting temperature to be a linear function of pressure under the given conditions, find what fraction of the ice melted. The specific volume of water is less than that of ice by ΔV' = 0.09 cm3/g.
Solution. 211. As before (Q.206) the lowering of melting point is given by
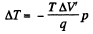
The superheated ice will then melt in part. The fraction that will melt is
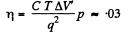
Q. 212. In the vicinity of the triple point the saturated vapour pressure p of carbon dioxide depends on temperature T as log p = a — bIT, where a and b are constants. If p is expressed in atmospheres, then for the sublimation process a = 9.05 and b = 1.80 kK, and for the vaporization process a = 6.78 and b = 1.31 kK. Find:
(a) temperature and pressure at the triple point;
(b) the values of the specific latent heats of sublimation, vaporization, and melting in the vicinity of the triple point.
Solution. 212. (a) The equations of the transition lines are

At the triple point they intersect Thus
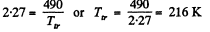
corresponding 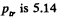 atmosphere.
atmosphere.
In the formula log 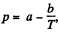 we compare b with the corresponding term in the equation in Q.210. Then
we compare b with the corresponding term in the equation in Q.210. Then
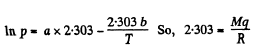
or, 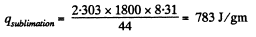
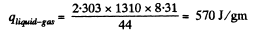
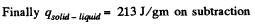
Q. 213. Water of mass m = 1.00 kg is heated from the temperature t1 = 10°C up to t2 = 100°C at which it evaporates completely. Find the entropy increment of the system.
Solution. 213.
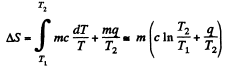
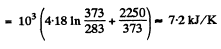
Q. 214. The ice with the initial temperature t1 = 0°C was first melted, then heated to the temperature t2 = 100°C and evaporated. Find the increment of the system's specific entropy.
Solution. 214.
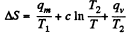
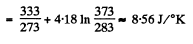
Q. 215. A piece of copper of mass m = 90 g at a temperature t1 = 90°C was placed in a calorimeter in which ice of mass 50 g was at a temperature —3°C. Find the entropy increment of the piece of copper by the moment the thermal equilibrium is reached.
Solution. 215. c = specific heat of copper = 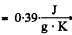 Suppose all ice does not melt, then
Suppose all ice does not melt, then
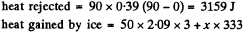
Thus x = 8-5 gm
The hypothesis is correct and final temperature will be T = 273K.
Hence change in entropy of copper piece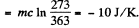
Q. 216. A chunk of ice of mass m1 = 100 g at a temperature t1 = 0°C was placed in a calorimeter in which water of mass m2 = 100 g was at a temperature t2. Assuming the heat capacity of the calorimeter to be negligible, find the entropy increment of the system by the moment the thermal equilibrium is reached. Consider two cases: (a) t2 = 60°C; (b) t2 = 94°C.
Solution. 216. (a) Here t2 = 60°C. Suppose the final temperature is t°C. Then
heat lost by water = m2c (t2 -1)
heat gained by ice = m1qm + m1c (t - t1), if all ice melts
In this case m1 qm = m2 x 4.18 (60 - t)y for m1 = m2
So the final temperature will be 0°C and only some ice will melt.
Then 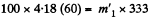
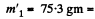 amount of ice that will melt
amount of ice that will melt
Finally 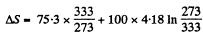
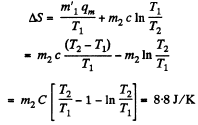
(b) 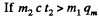 then all ice will melt as one can check and the final temperature can be obtained like this
then all ice will melt as one can check and the final temperature can be obtained like this
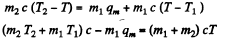
or 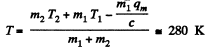
and 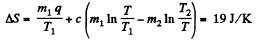
Q. 217. Molten lead of mass m = 5.0 g at a temperature t2 = 327°C (the melting temperature of lead) was poured into a calorimeter packed with a large amount of ice at a temperature t1 = 0°C. Find the entropy increment of the system lead-ice by the moment the thermal equilibrium is reached. The specific latent heat of melting of lead is equal to q = 22.5 J/g and its specific heat capacity is equal to c = 0.125 J/(g • K).
Solution. 217. 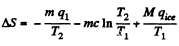
where 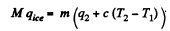
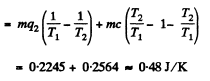
Q. 218. A water vapour filling the space under the piston of a cylinder, is compressed (or expanded) so that it remains saturated all the time, being just on the verge of condensation. Find the molar heat capacity C of the vapour in this process as a function of temperature T, assuming the vapour to be an ideal gas and neglecting the specific volume of water in comparison with that of vapour. Calculate C at a temperature t = 100°C.
Solution. 218. When heat dQ is given to the vapour its temperature will change by dT, pressure by dp and volume by dV, it being assumed that the vapour remains saturated.
Then by C-C equation
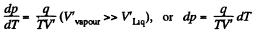
on the other hand, 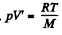
So 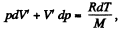
Hence 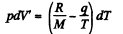
finally 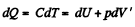
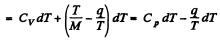
(Cp, Cv refer to unit mass here). Thus
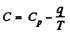
For water 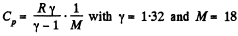
So 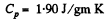
and 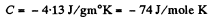
Q. 219. One mole of water being in equilibrium with a negligible amount of its saturated vapour at a temperature T1 was completely converted into saturated vapour at a temperature T2. Find the entropy increment of the system. The vapour is assumed to be an ideal gas, the specific volume of the liquid is negligible in comparison with that of the vapour.
Solution. 219. The required entropy change can be calculated along a process in which the water is heated from T1 to T2 and then allowed to evaporate. The entropy change for this is
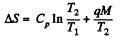
where q = specific latent heat of vaporization.
|
95 videos|367 docs|98 tests
|
















