JEE Advanced (Subjective Type Questions): Differentiation | Mathematics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
Q.1. Find the derivative of sin (x2 + 1) with respect to x from first principle.
Ans. 2 x cos (x2 + 1)
Solution. Let f (x) = sin (x2 + 1) then

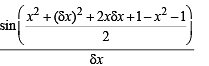
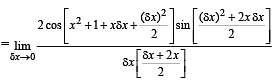
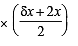
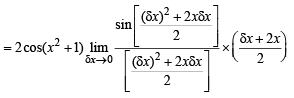

Q.2. Find the derivative of

Ans. -2/9
Solution.
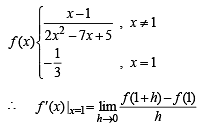
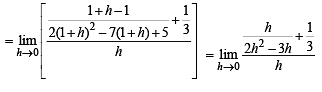

Q.3.
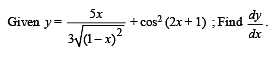
Ans.
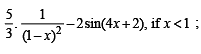
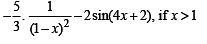
Solution. We have, 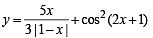
(Clearly y is not defined at x = 1)
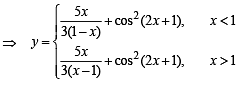
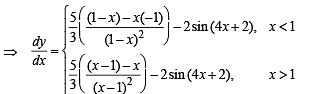
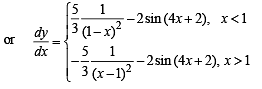
Q. 4. 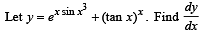
Ans. 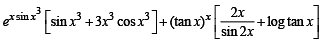
Solution. We are given 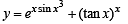
Here y is the sum of two functions and in the second function base as well as power are functions of x. Therefore we will use logarithmic differentiation here.
Let y = u + v
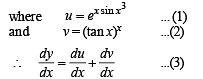
Differentiating (1) with respect to x, we get
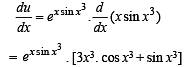
Taking log on both sides on equn (2), we get
log v = x log tan x
Differentiating the above with respect to x, we get
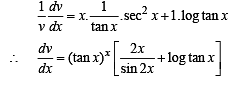
Substituting the value of 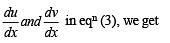

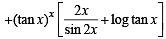
Q. 5. Let f be a twice differentiable function such that
f "(x) = – f (x), and f '(x)= g (x), h(x) = [f (x)]2 + [g (x)]2
Find h(10) if h(5) = 11
Ans. 11
Solution. Given that f is twice differentiable such that
f " (x) = – f (x) and f '(x) = g(x)
h (x) = [f (x)]2 + [g (x)]2
To find h (10) when h (5) = 11.
Consider h'(x) = 2f f ' + 2gg' = 2f (x) g(x) + 2g(x)f " (x)
[∴ g(x) = f '(x) ⇒ g' (x) = f ''(x)]
= 2f (x) g (x) + 2g(x) (– f (x))
= 2f (x) g (x) – 2f (x) g (x) = 0

⇒ h is a constant function
∴ h (5) = 11 ⇒ h (10) = 11.
Q. 6. If a be a repeated root of a quadratic equation f(x) = 0 and A(x), B(x) and C(x) be polynomials of degree 3, 4 and 5 respectively, then show that 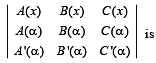 divisible by f(x), where prime denotes the derivatives.
divisible by f(x), where prime denotes the derivatives.
Solution.
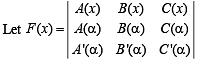
Given that α is a repeated root of quadratic equation f (x) = 0
∴ We must have f (x) = k (x – α)2 ; where k is a non- zero real no.
If we put x = α on both sides of eq. (1); we get
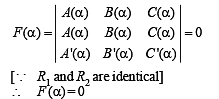
Hence (x – α) is a factor of F(x) Differentiating eq. (1) w.r. to x, we get
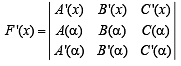
Putting x = α on both sides, we get
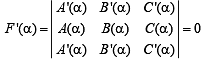
[as R1 and R3 are identical]
⇒ (x – α) is a factor of F'(x) al so. Or we can say (x – α)2 is a factor of F(x).
⇒ F (x) is divisible by f (x).
Q. 7. If x = sec θ – cos θ and y = secn θ - cosn θ , then show that 
Solution. We have, x = sec θ – cos θ, y = secn θ – cosn θ

sec θ tan θ + tan θ cos θ = tan θ (sec θ + cos θ)
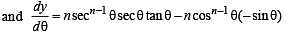
= n secn θ tan θ +n tan θ cosn θ = n tan θ (secn θ + cosn θ)
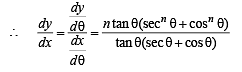
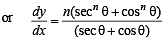 ...(1)
...(1)
Also x2 + 4 = (sec θ – cos θ)2 + 4
= sec2 θ + cos2 θ – 2 sec θ cos θ + 4
= sec2 θ + cos2 θ + 2
= (sec θ + cos θ)2 ...(2)
and y2 + 4 = secn θ – cosn θ)2 + 4
= sec2n θ + cos2n θ – 2 secn θ cosn θ + 4
= sec 2n θ + cos 2n θ + 2
= (secn θ + cosn θ)2 ...(3)
Now we have to prove
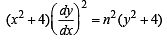
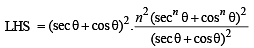
[Using (1) and (2)]
= n2 (secn q + cosn q)2
= n2 (y2 + 4) [From eq. (3)]
= RHS
Q. 8. Find dy/dx at x = – 1, when

Ans. 0
Solution. We have given the function
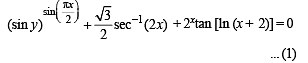
For x = – 1, we have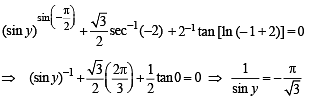
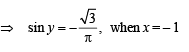 ....(2)
....(2)
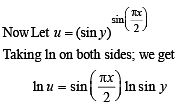
Differentiating both sides with respect to x, we get

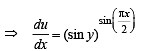
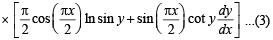
Now differentiating eq. (1), we get
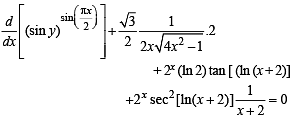
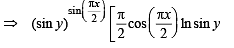

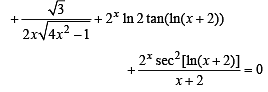
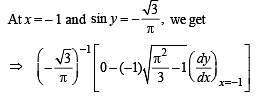
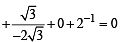
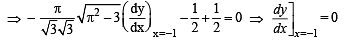
Q. 9. 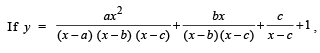
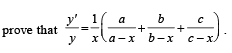
Solution.

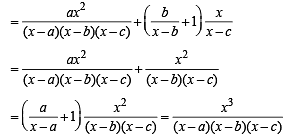
⇒ log y = 3 log x – log (x – a) – log (x – b) – log (x – c)
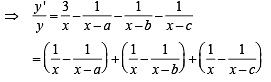
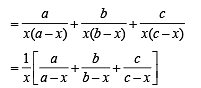
|
149 videos|192 docs|197 tests
|

|
Explore Courses for Airforce X Y / Indian Navy SSR exam
|

|

















