Lakhmir Singh & Manjit Kaur: Gravitation, Solutions- 2 | Science Class 9 PDF Download
Page No - 101
Question 26:
Fill in the following blanks with suitable words :
(a) The acceleration due to gravity on the moon is about………………………. of that on the earth.
(b) In order that the force of gravitation between two bodies may become noticeable and cause motion, one of the bodies must have an extremely large……………………………..
(c) The weight of an object on the earth is about……………….. of its weight on the moon.
(d) The weight of an object on the moon is about …………………….. of its weight on the earth.
(e) The value of g on the earth is about………………. of that on the moon.
(f) If the weight of a body is 6 N on the moon, it will be about……………………… on the earth.
Solution :
(a) One-sixth
(b) Mass
(c) Six times
(d) One-sixth
(e) Six times
(f) 36N
Question 27:
Explain what is meant by the equation :
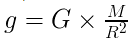
where the symbols have their usual meanings.
Solution :
This is the acceleration produced by the earth. It is also called acceleration due to gravity.
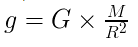
where, G= gravitational constant
M= mass of the earth.
R=radius of the earth
Question 28:
(a) What do you mean by the term ‘free fall’ ?
(b) During a free fall, will heavier objects accelerate more than lighter ones ?
Solution :
(a) The falling of a body from a height towards the earth under the gravitational force of the earth (with no other forces acting on it) is called free fall.
(b) No, acceleration is independent of the mass of the body during free fall.
Question 29:
Can we apply Newton’s third law to the gravitational force ? Explain your answer.
Solution :
Yes, Newton’s third law of motion holds good for the force of gravitation. This means that when earth exerts a force of attraction on an object, then the object also exerts an equal force on the earth, in the opposite direction.
Question 30:
Give reason for the following :
The force of gravitation between two cricket balls is extremely small but that between a cricket ball and the earth is extremely large.
Solution :
The force of gravitation between two bodies is directly proportional to the product of their masses.
F ∝ m x M
Since the mass of cricket balls is very small as compared to that of the earth, so the force of gravitation between two cricket balls is extremely small while that between a ball and the earth is extremely large.
Question 31:
Describe how the gravitational force between two objects depends on the distance between them.
Solution :
The gravitational force F between two bodies of masses M and m kept at a distance d from each other is :

the force between two bodies is inversely proportional to the square of the distance between them. That is,
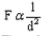
Therefore , if we double the distance between two bodies, the gravitational force becomes one-fourth and if we halve the distance between two bodies, then the gravitational force becomes four times .
Question 32:
What happens to the gravitational force between two objects when the distance between them is :
(i) doubled ?
(ii) halved ?
Solution :
(a)If we double the distance between two bodies, the gravitational force becomes one-fourth.
(b)If we halve the distance between two bodies, then the gravitational force becomes four times.
Question 33:
State two applications of universal law of gravitation.
Solution :
(i) Universal law of gravitation is used to determine the masses of the sun, the earth and the moon accurately.
(ii) Universal law of gravitation helps in discovering new stars and planets.
Question 34:
Explain why, if a stone held in our hand is released, it falls towards the earth.
Solution :
This is because the earth exerts a force of attraction (called gravity) on the stone and pulls it down.
Question 35:
Calculate the force of gravitation between two objects of masses 50 kg and 120 kg respectively kept at a distance of 10 m from one another. (Gravitational constant, G = 6.7 x 10-11 Nm2 kg-2)
Solution
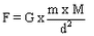
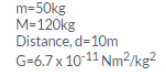
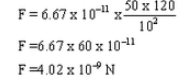
Question 36:
What is the force of gravity on a body of mass 150 kg lying on the surface of the earth? (Mass of earth = 6 x 1024 kg; Radius of earth = 6.4 x 106 m; G = 6.7 x 10-11 Nm2/kg2)
Solution :
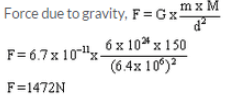
Question 37:
The mass of sun is 2 x 1030 kg and the mass of earth is 6 x 1024 If the average distance between the sun and the earth be 1.5 x 108 km, calculate the force of gravitation between them.
Solution :
Distance d=1.5 x 108km= 1.5 x 1011 m
Mass of the sun, m=2×1030kg
Mass of the earth, M = 6 x 1024Kg
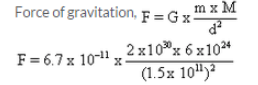
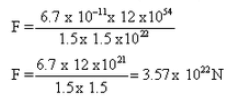
Question 38:
A piece of stone is thrown vertically upwards. It reaches the maximum height in 3 seconds. If the acceleration of the stone be 9.8 m/s2 directed towards the ground, calculate the initial velocity of the stone with which it is thrown upwards
Solution :
Initial velocity of the stone, u=?
Final velocity of
stone, v=0
Acceleration due to gravity, g= -9.8m/s2
Time, t=3 sec
Using relation, v=u + gt
0 = u -9.8 x 3
u =29.4m/s
Question 39:
A stone falls from a building and reaches the ground 2.5 seconds later. How high is the building ? (g =8 m/s2)
Solution :
Initial velocity,
u=0m/s
Acceleration due to
gravity, g=9.8m/s2
Time taken to reach
the ground, t=2.5 sec
Height, h=?
Using relation,
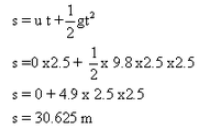
Question 40:
A stone is dropped from a height of 20 m.
(i) How long will it take to reach the ground ?
(ii) What will be its speed when it hits the ground ? (g =10 m/s2)
Solution :
Height, s=20m
Initial velocity, u=0
Acceleration due to gravity, g=10m/s2
Final velocity, v=?
Time taken, t=?
(i) Using relation,
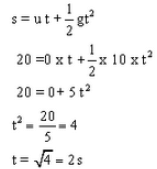
(ii) For a freely falling body:
v2 = u2 + 2gh
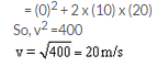
The speed of stone when it hits the ground will be 20m/s.
Question 41:
A stone is thrown vertically upwards with a speed of 20 m/s. How high will it go before it begins to fall ? (g =8 m/s2)
Solution :
Initial velocity, u=20m/s
Final velocity, v=0
Acceleration due to gravity, g=-9.8m/s2
Height, h=?
Using relation, for a freely falling body:
v2 = u2 + 2gh
(0)2 = (20)2 + 2 x (-9.8) x h
0-400 = -19.6 h
h= 400/19.6 = 20.4 m
Question 42:
When a cricket ball is thrown vertically upwards, it reaches a maximum height of 5 metres.
(a) What was the initial speed of the ball ?
(b) How much time is taken by the ball to reach the highest point ? (g=10 ms-2)
Solution :
Initial velocity, u=?
Final velocity, v=0
Acceleration due to gravity, g=-10m/s2
Height, h=5 m
(a) For a freely falling body:
v2 = u2 + 2gh
(0)2 = u2+ 2 x(-10)x 5
0= u2 -100
u2= 100
So, u=10m/s
(b) Using relation, v=u + gt
0 = 10 + (-10) t
-10= -10 t
t=1sec
Question 43:
Write the differences between mass and weight of an object.
Solution :
Mass | Weight |
1. The of an object is the quantity of matter contained in it. | 1. The weight of an object is the force with which it is attracted toward the centre of the earth. |
2. SI Unit of Mass is Killogram (Kg). | SI unit of weight is Newton(N) |
3. the mass of an object is constant | The weight of an object can be zero |
Question 44:
Can a body have mass but no weight ? Give reasons for your answer.
Solution :
Yes, weight of a body is not constant, it varies with the value of acceleration due to gravity, g.
Weight of a body is zero, when it is taken to the centre of the earth or in the interplanetary space, where g=0.
Page No - 102
Question 45:
A force of 20 N acts upon a body whose weight is 9.8 N. What is the mass of the body and how much is its acceleration ? (g = 9.8 m s-2).
Solution :
Weight= 9.8N
W= m x g
9.8 =m x 9.8
m= 1kg
Force, F= mass x acceleration
20 N = 1kg x a
Acceleration,
a=20m/s2
Question 46:
A stone resting on the ground has a gravitational force of 20 N acting on it. What is the weight of the stone ? What is its mass ? (g = 10 m/s2).
Solution :
Weight of the stone = Gravitational force acting on it = 20 N
Weight, W= m x g
20=m x 10
m=2 kg
Question 47:
An object has mass of 20 kg on earth. What will be its (i) mass, and (ii) weight, on the moon ? (g on moon = 1.6 m/s2).
Solution :
(i) Its mass will be 20 kg as mass is a constant quantity.
(ii)Weight, W= m x g =20 x 1.6=32N
Question 48:
Which is more fundamental, the mass of a body or its weight ? Why ?
Solution :
The mass of a body is more fundamental because mass of a body is constant and does not change from place to place.
Question 49:
How much is the weight of an object on the moon as compared to its weight on the earth ? Give reason for your answer


It is quite difficult to lift heavy weight on earth but it becomes very easy to lift the same heavy weight on the moon. why?
Solution :
The weight of an object on the moon is about one-sixth of its weight on the earth. This is because the value of acceleration due to gravity on the moon is about
one-sixth of that on the earth.
Question 50:
(a) Define mass of a body. What is the SI unit of mass ?
(b) Define weight of a body. What is the SI unit of weight ?
(c) What is the relation between mass and weight of a body ?
Solution :
(a) The mass of a body is the quantity of matter contained in it. The SI unit of mass is kilogram (kg).
(b) The weight of a body is the force with which it is attracted towards the centre of the earth. The SI unit of weight is newton (N).
(c) Weight, W =m x g, i.e. the weight of a body is directly proportional to its mass.
Question 51:
(a) State the universal law of gravitation. Name the scientist who gave this law.
(b) Define gravitational constant. What are the units of gravitational constant ?
Solution :
(a) According to universal law of gravitation: Every body in the universe attracts every other body with a force (F) which is directly proportional to the product of their masses (m and M) and inversely proportional to the square of the distance (d) between them.

(b) The gravitational constant G is numerically equal to the force of gravitation which exists between two bodies of unit masses kept at a unit distance from each other.

Sir Isaac Newton gave this law.
Question 52:
(a) What do you understand by the term ‘acceleration due to gravity of earth’ ?
(b) What is the usual value of the acceleration due to gravity of earth ?
(c) State the SI unit of acceleration due to gravity.
Solution :
(a) The uniform acceleration produced in a freely falling body due to the gravitational force of the earth is called acceleration due to gravity of earth.
(b) Usual value of acceleration due to gravity, g=9.8 m/s2.
(c) SI unit of acceleration due to gravity is m/s2.
Question 53:
(a) Is the acceleration due to gravity of earth ‘g’ a constant ? Discuss.
(b) Calculate the acceleration due to gravity on the surface of a satellite having a mass of 7.4 x 1022 kg and a radius of 1.74 x 106 m (G = 6.7 x 10-11 Nm2/kg2). Which satellite do you think it could be ?
Solution :
(a) No, the value of acceleration due to gravity (g) is not constant at all the places on the surface of the earth. Since the radius of the earth is minimum at the poles and maximum at the equator, the value of g is maximum at the poles and minimum at the equator. As we go up from the surface of the earth, the distance from the centre of the earth increases and hence the value of g decreases. The value of g also decreases as we go down inside the earth.


As the value of g = 1.637m/s2 , which is one sixth of the value of g on earth, the satellite could be moon.
Question 54:
State and explain Kepler’s laws of planetary motion. Draw diagrams to illustrate these laws.
Solution :
Kepler’s first law: The planets move in elliptical orbits around the sun, with the sun at one of the two foci of the elliptical orbit. This law means that the orbit of a planet around the sun is an ellipse and not an exact circle. An elliptical path has two foci, and the sun is at one of the two foci of the elliptical path.
Kepler’s Second law states that: Each planet revolves around the sun in such a way that the line joining the planet to the sun sweeps over equal areas in equal intervals of time. This means that a planet does not move with constant speed around the sun. The speed is greater when the planet is nearer the sun, and less when the planet is farther away from the sun.
Kepler’s Third Law states that: The cube of the mean distance of a planet from the sun is directly proportional to the square of time it takes to move around the sun.
Kepler's first law : the planet move in elliptical orbits around the sun, with the sun at one of the two foci of elliptical orbit. This law means that the orbit of a planet around the sun is an ellipse and not an exact circle. An elliptical path has two foci, and the sun is at one of the two foci of the elliptical path.

Kepler's second law state that : Each planet revolve around the sun in such a way that the line joining the planet to the sun sweeps over equal areas in equal intervals of time. This mean that a planet does not move with constant speed around the sun. The speed is greater when the planet nearer the sun, and less when the planet is farther away from the sun.

Kepler's third law sate that : The cube of the mean distance of planet from the sun is directly proportional to the square of time it takes to move around the sun.

Question 55:
The mass of a planet is 6 x 1024 kg and its diameter is 12.8 x 103 If the value of gravitational constant be 6.7 x 10-11 Nm2/kg2, calculate the value of acceleration due to gravity on the surface of the planet. What planet could this be ?
Solution :
Acceleration due to gravity,


As the value of g = 9.8m/s2, the planet could be earth.
Page No - 103
Question 71:
If the distance between two masses is increased by a factor of 5, by what factor would the mass of one of them have to be altered to maintain the same gravitational force ? Would this be an increase or decrease in the mass ?
Solution :
Gravitational force is given by:

Distance between two masses is increased s.t new distance is D = 5d
New Gravitational force F1 = F
Let on of the mass is changed to m1 so as to maintain the same gravitational force


Hence the mass should be increased by 25 times in order to have the same gravitational force.
Question 72:
Universal law of gravitation states that every object exerts a gravitational force of attraction on every other object. If this is true, why don’t we notice such forces ? Why don’t the two objects in a room move towards each other due to this force ?

The universal law of gravitation states that every object exerts a gravitational force of attraction on every other object. if this is true, then why don't we see the various objects in a room moving toward one another?
Solution :
In order to be able to notice the gravitational force of attraction between any two objects, at least one of the objects on the earth should have an extremely large mass. Since no object on the earth have an extremely large mass, we cannot notice such forces.
The two objects in a room do not move towards each other because due to their small masses, the gravitational force of attraction between them is very, very weak.
Question 73:
Suppose a planet exists whose mass and radius both are half those of the earth. Calculate the acceleration due to gravity on the surface of this planet.
Solution :
Acceleration due to gravity of earth,

Acceleration due to gravity on the surface of planet will be :


Page No:104
Question 74:
A coin and a piece of paper are dropped simultaneously from the same height. Which of the two will touch the ground first ? What will happen if the coin and the piece of paper are dropped in vacuum ? Give reasons for your answer.
Solution :
The coin reaches the ground first as compared to the piece of paper because it experiences lesser resistance from air than that felt by paper.
If the coin and the piece of paper are dropped in vacuum, both of them will touch the ground at the same time.
Question 75:
A stone and the earth attract each other with an equal and opposite force. Why then we see only the stone falling towards the earth but not the earth rising towards the stone ?
Solution :
The mass of a stone is very small, due to which the gravitational force produces a large acceleration in it. Due to large acceleration of stone, we see stone falling towards the earth. The mass of earth is, however, very, very large. Due to the very large mass of the earth, the same gravitational force produces very, very small acceleration in the earth, that it cannot be observed. And hence we do not see the earth rising up towards the stone.
Question 76:
What is the actual shape of the orbit of a planet around the sun ? What assumption was made by Newton regarding the shape of an orbit of a planet around the sun for deriving his inverse square rule from Kepler’s third law of planetary motion ?
Solution :
The actual shape of the orbit of a planet around the sun is elliptical. The assumption made by the Newton regarding the shape of an orbit of a planet around the sun was that the orbit of a planet around the sun is ‘circular’.
Question 77:
The values of g at six distances A, B, C, D, E and F from the surface of the earth are found to be 3.08 m/s2, 9.2.3 m/s2, 0.57 m/s2, 7.34 m/s2, 0.30 m/s2 and 1.49 m/s2, respectively.
(a) nArrange these values of g according to the increasing distances from the surface of the earth (keeping the value of g nearest to the surface of the earth first)
(b) If the value of distance F be 10000 km from the surface of the earth, state whether this distance is deep . inside the earth or high up in the sky. Give reason for your answer.
Solution :
(a) 9.23 m/s2 , 7.34 m/s2 , 3.08 m/s2 , 1.49 m/s2 , 0.57 m/s2 , 0.30 m/s2
(b) This distance F of 10000 km is high up in the sky. The distance of 10000 km cannot be deep inside the earth because the radius of earth is only about 6400km and the value of g at the centre of earth becomes zero.
|
88 videos|369 docs|67 tests
|
FAQs on Lakhmir Singh & Manjit Kaur: Gravitation, Solutions- 2 - Science Class 9
| 1. What is the formula for gravitational force? |  |
| 2. What is the difference between mass and weight? |  |
| 3. What is free fall? |  |
| 4. How does the gravitational force between two objects change with distance? |  |
| 5. What is the difference between gravitational field and gravitational force? |  |

|
Explore Courses for Class 9 exam
|

|


















