Ex-6.9, Fractions, Class 6, Maths RD Sharma Solutions | RD Sharma Solutions for Class 6 Mathematics PDF Download
Q1: Add :
(i) 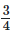 and
and 
(ii) 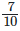 and
and 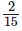
(iii) 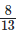 and
and 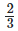
(iv) 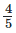 and
and 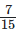
Ans:
(i) 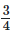 and
and 
It can be written as
3/4 + 5/6
We know that the LCM of 4 and 6 is 12
In order to convert fraction into equivalent fraction having 12 as denominator
= [(3 × 3)/ (4 × 3)] + [(5 × 2)/ (6 × 2)]
On further calculation
= 9/12 + 10/ 12
We get
= (9 + 10)/ 12 = 19/12
(ii) 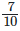 and
and 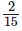
It can be written as
7/10 + 2/15
We know that the LCM of 10 and 15 is 30
In order to convert fraction into equivalent fraction having 30 as denominator
= [(7 × 3)/ (10 × 3)] + [(2 × 2)/ (15 × 2)]
On further calculation
= 21/30 + 4/ 30
We get
= (21 + 4)/ 30 = 25/30 = 5/6
(iii) 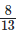 and
and 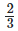
It can be written as
8/13 + 2/3
We know that the LCM of 13 and 3 is 39
In order to convert fraction into equivalent fraction having 39 as denominator
= [(8 × 3)/ (13 × 3)] + [(2 × 13)/ (3 × 13)]
On further calculation
= 24/39 + 26/39
We get
= (24 + 26)/ 39 = 50/39
(iv) 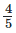 and
and 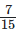
It can be written as
4/5 + 7/15
We know that the LCM of 5 and 15 is 1
In order to convert fraction into equivalent fraction having 15 as denominator
= [(4 × 3)/ (5 × 3)] + [(7 × 1)/ (15 × 1)]
On further calculation
= 12/15 + 7/ 15
We get
= (12 + 7)/ 15 = 19/15
Q2: Subtract :
(i) 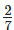 from
from 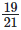
(ii)  from
from 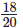
(iii) 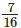 from
from 
(iv) 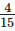 from
from 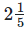
Ans:
(i) 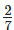 from
from 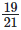
It can be written as
19/21 – 2/7
We know that LCM of 21 and 7 is 21
In order to convert fraction into equivalent fraction having 21 as denominator
= [(19 × 1)/ (21 × 1)] – [(2 × 3)/ (7 × 3)]
On further calculation
= 19/21 – 6/21
We get
= (19 – 6)/21 = 13/21
(ii)  from
from 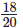
It can be written as
18/20 – 21/25
We know that LCM of 20 and 25 is 100
In order to convert fraction into equivalent fraction having 100 as denominator
= [(18 × 5)/ (20 × 5)] – [(21 × 4)/ (25 × 4)]
On further calculation
= 90/100 – 84/100
We get
= (90 – 84)/100 = 6/100 = 3/50
(iii) 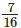 from
from 
It can be written as
2/1 – 7/16
We know that LCM of 1 and 16 is 16
In order to convert fraction into equivalent fraction having 16 as denominator
= [(16 × 2)/ (16 × 1)] – [(7 × 1)/ (16 × 1)]
On further calculation
= 32/16 – 7/16
We get
= (32 – 7)/16 = 25/16
(iv) 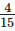 from
from 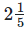
It can be written as
11/5 – 4/15
We know that LCM of 5 and 15 is 15
In order to convert fraction into equivalent fraction having 15 as denominator
= [(11 × 3)/ (5 × 3)] – [(4 × 1)/ (15 × 1)]
On further calculation
= 33/15 – 4/15
We get
= (33 – 4)/15 = 29/15
Q3: Find the difference of :
(i) 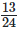 and
and 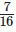
(ii)  and
and 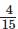
(iii) 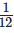 and
and 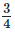
(iv) 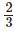 and
and 
Ans:
(i) 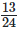 and
and 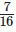
It can be written as
13/24 – 7/16
We know that LCM of 24 and 16 is 48
In order to convert fraction into equivalent fraction having 48 as denominator
= [(13 × 2)/ (24 × 2)] – [(7 × 3)/ (16 × 3)]
On further calculation
= 26/48 – 21/48
We get
= (26 – 21)/48 = 5/48
(ii)  and
and 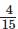
It can be written as
5/18 – 4/15
We know that LCM of 18 and 15 is 90
In order to convert fraction into equivalent fraction having 90 as denominator
= [(5 × 5)/ (18 × 5)] – [(4 × 6)/ (15 × 6)]
On further calculation
= 25/90 – 24/90
We get
= (25 – 24)/90 = 1/90
(iii) 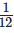 and
and 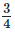
It can be written as
3/4 – 1/12
We know that LCM of 4 and 12 is 12
In order to convert fraction into equivalent fraction having 12 as denominator
= [(3 × 3)/ (4 × 3)] – [(1 × 1)/ (12 × 1)]
On further calculation
= 9/12 – 1/12
We get
= (9 – 1)/12 = 8/12 = 2/3
(iv) 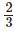 and
and 
It can be written as
6/7 – 2/3
We know that LCM of 7 and 3 is 21
In order to convert fraction into equivalent fraction having 48 as denominator
= [(6 × 3)/ (7 × 3)] – [(2 × 7)/ (3 × 7)]
On further calculation
= 18/21 – 14/21
We get
= (18 – 14)/21 = 4/21
Q4: Subtract as indicated :
(i) 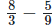
(ii) 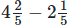
(iii) 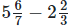
(iv) 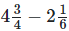
Ans:
(i) 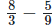
It can be written as
8/3 – 5/9
We know that LCM of 3 and 9 is 9
In order to convert fraction into equivalent fraction having 9 as denominator
= [(8 × 3)/ (3 × 3)] – [(5 × 1)/ (9 × 1)]
On further calculation
= 24/9 – 5/9
We get
= (24 – 5)/9 = 19/9
(ii) 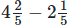
It can be written as
22/5 – 11/5
We get
= (22 – 11)/5 = 11/5
(iii) 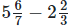
It can be written as
41/7 – 8/3
We know that LCM of 7 and 3 is 21
In order to convert fraction into equivalent fraction having 21 as denominator
= [(41 × 3)/ (7 × 3)] – [(8 × 7)/ (3 × 7)]
On further calculation
= 123/21 – 56/21
We get
= (123 – 56)/21 = 67/21
(iv) 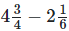
It can be written as
19/4 – 13/6
We know that LCM of 4 and 6 is 12
In order to convert fraction into equivalent fraction having 12 as denominator
= [(19 × 3)/ (4 × 3)] – [(13 × 2)/ (6 × 2)]
On further calculation
= 57/12 – 26/12
We get
= (57 – 26)/12 = 31/12
Q5: Simplify:
simplify :
(i) 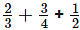
(ii) 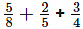
(iii) 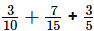
(iv) 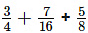
(v) 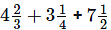
(vi) 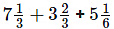
(vii) 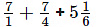
(viii) 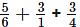
(ix) 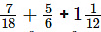
Ans:
(i) 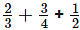
We know that the LCM of 3, 4 and 2 is 12
In order to convert fraction into equivalent fraction having 12 as denominator
= [(2 × 4)/ (3 × 4)] + [(3 × 3)/ (4 × 3)] + [(1 × 6)/ (2 × 6)]
On further calculation
= 8/12+ 9/12 + 6/12
We get
= (8 + 9 + 6)/ 12 = 23/12
(ii) 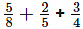
We know that the LCM of 8, 5 and 4 is 40
In order to convert fraction into equivalent fraction having 40 as denominator
= [(5 × 5)/ (8 × 5)] + [(2 × 8)/ (5 × 8)] + [(3 × 10)/ (4 × 10)]
On further calculation
= 25/40 + 16/40 + 30/40
We get
= (25 + 16 + 30)/ 40 = 71/40
(iii) 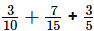
We know that the LCM of 10, 15 and 5 is 30
In order to convert fraction into equivalent fraction having 30 as denominator
= [(3 × 3)/ (10 × 3)] + [(7 × 2)/ (15 × 2)] + [(3 × 6)/ (5 × 6)]
On further calculation
= 9/30+ 14/30 + 18/30
We get
= (9 + 14 + 18)/ 30 = 41/30
(iv) 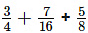
We know that the LCM of 4, 16 and 8 is 16
In order to convert fraction into equivalent fraction having 16 as denominator
= [(3 × 4)/ (4 × 4)] + [(7 × 1)/ (16 × 1)] + [(5 × 2)/ (8 × 2)]
On further calculation
= 12/16 + 7/16 + 10/16
We get
= (12 + 7 + 10)/ 16 = 29/16
(v) 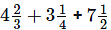
It can be written as
14/3 + 13/4 + 15/2
We know that the LCM of 3, 4 and 2 is 12
In order to convert fraction into equivalent fraction having 12 as denominator
= [(14 × 4)/ (3 × 4)] + [(13 × 3)/ (4 × 3)] + [(15 × 6)/ (2 × 6)]
On further calculation
= 56/12 + 39/12 + 90/12
We get
= (56 + 39 + 90)/ 12 = 185/12
(vi) 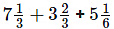
It can be written as
22/3 + 11/3 + 31/6
We know that the LCM of 3, 3 and 6 is 6
In order to convert fraction into equivalent fraction having 6 as denominator
= [(22 × 2)/ (3 × 2)] + [(11 × 2)/ (3 × 2)] + [(31 × 1)/ (6 × 1)]
On further calculation
= 44/6 + 22/6 + 31/6
We get
= (44 + 22 + 31)/ 6 = 97/6
(vii) 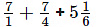
It can be written as
7/1 + 7/4 + 31/6
We know that the LCM of 1, 4 and 6 is 12
In order to convert fraction into equivalent fraction having 12 as denominator
= [(7 × 12)/ (1 × 12)] + [(7 × 3)/ (4 × 3)] + [(31 × 2)/ (6 × 2)]
On further calculation
= 84/12 + 21/12 + 62/12
We get
= (84 + 21 + 62)/12 = 167/12
(viii) 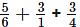
We know that the LCM of 6, 1 and 4 is 12
In order to convert fraction into equivalent fraction having 12 as denominator
= [(5 × 2)/ (6 × 2)] + [(3 × 12)/ (1 × 12)] + [(3 × 3)/ (4 × 3)]
On further calculation
= 10/12 + 36/12 + 9/12
We get
= (10 + 36 + 9)/ 12 = 55/12
(ix) 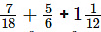
It can be written as
7/18 + 5/6 + 13/12
We know that the LCM of 18, 6 and 12 is 36
In order to convert fraction into equivalent fraction having 12 as denominator
= [(7 × 2)/ (18 × 2)] + [(5 × 6)/ (6 × 6)] + [(13 × 3)/ (12 × 3)]
On further calculation
= 14/36 + 30/36 + 39/36
We get
= (14 + 30 + 39)/36 = 83/36
Q6: Replace * by the correct number:
(i) * – 5/8 = 1/4
(ii) * – 1/5 = 1/2
(iii) 1/2 – * = 1/6
Ans:
(i) * – 5/8 = 1/4
It can be written as
* = 1/4 + 5/8
On further calculation
* = [(1 × 2)/ (4 × 2)] + [(5 × 1)/ (8 × 1)]
We get
* = 2/8 + 5/8
By addition
*= (2 + 5)/ 8 = 7/8
(ii) * – 1/5 = 1/2
It can be written as
* = 1/2 + 1/5
On further calculation
* = [(1 × 5)/ (2 × 5)] + [(1 × 2)/ (5 × 2)]
We get
* = 5/10 + 2/10
By addition
* = (2 + 5)/ 10 = 7/10
(iii) 1/2 – * = 1/6
It can be written as
* = 1/2 – 1/6
On further calculation
* = [(1 × 3)/ (2 × 3)] – [(1 × 1)/ (6 × 1)]
We get
* = 3/6 – 1/6
By addition
* = (3 – 1)/ 6 = 2/6 = 1/3
Q7: Savita bought 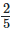 m of ribbon and kavita
m of ribbon and kavita 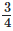 m of ribbon. What was the total length of the ribbon they bought ?
m of ribbon. What was the total length of the ribbon they bought ?
Ans:
Length of ribbon Savita bought = 2/5 m
Length of ribbon Kavita bought = 3/4 m
So the total length of ribbon they bought = 2/5 + 3/4
We know that the LCM of 5 and 4 is 20
So we get
= [(2 × 4)/ (5 × 4)] + [(3 × 5)/ (4 × 5)]
On further calculation
= 8/20 + 15/20
We get
= (8 + 15)/20 = 23/20 m
Hence, the total length of the ribbon they bought is 23/20 m.
Q8: Ravish takes 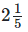 minutes to walk across the school ground. Rahul takes
minutes to walk across the school ground. Rahul takes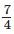 minutes to do the same. Who takes less time and by what fraction ?
minutes to do the same. Who takes less time and by what fraction ?
Ans: Time taken by Ravish to walk across the school ground = 2 1/5 minutes = 11/5 minutes
Time taken by Rahul to walk across the school ground = 7/4 minutes
By comparing 11/5 and 7/4 minutes
We know that LCM of 4 and 5 is 20
In order to convert fraction into equivalent fraction having 20 as denominator
[(11 × 4)/ (5 × 4)], [(7 × 5)/ (4 × 5)]
So we get 44/20 > 35/20
So Rahul takes less time
It can be written as
44/20 – 35/20 = (44 – 35)/20 = 9/20 minutes
Hence, Rahul takes less time by 9/20 minutes.
Q9: A piece of a wire 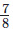 metres long broke into two pieces. One piece was
metres long broke into two pieces. One piece was 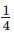 meter long. How long is the other piece ?
meter long. How long is the other piece ?
Ans:
It is given that
Length of wire = 7/8 m
Length of first piece = 1/4 m
Consider x m as the length of second piece
It can be written as
Length of wire = Length of first piece + Length of second piece
By substituting the values
7/8 = 1/4 + x
On further calculation
x = 7/8 – 1/4
We know that the LCM of 8 and 4 is 8
x = [(7 × 1)/ (8 × 1)] – [(1 × 2)/ (4 × 2)]
We get
x = 7/8 – 2/8
By subtraction
x = (7 – 2)/ 8 = 5/8 m
Hence, the length of second piece of wire is 5/8 m.
Q10: Shikha and priya have bookshelves of the same size shikha’s shelf is 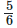 full of book and priya’s shelf is
full of book and priya’s shelf is 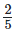 full. Whose bookshelf is more full ? By what fraction ?
full. Whose bookshelf is more full ? By what fraction ?
Ans: Fraction of Shikha’s shelf filled with books = 5/6
Fraction of Priya’s shelf filled with books = 2/5
We know that LCM of 5 and 6 is 30
In order to convert fraction into equivalent fraction having 30 as denominator
= [(5 × 5)/ (6 × 5)], [(2 × 6)/ (5 × 6)]
So we get 25/30 > 12/30
So Shikha’s shelf is more full.
It can be written as
25/30 – 12/30 = (25 – 12)/ 30 = 13/30
Hence, Shikha’s bookshelf is more full by 13/30.
Q11: Ravish’s house is 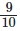 Km from his school. He walked some distance and then took a bus for
Km from his school. He walked some distance and then took a bus for 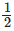 Km. How far did he walk?
Km. How far did he walk?
Ans:
It is given that
Distance of Ravish’s house from his school = 9/10 km
Distance covered by bus = 1/2 km
It can be written as
Distance between house and school = Distance covered by walking + Distance covered by bus
So we get
Distance covered by walking = Distance between house and school – Distance covered by bus
Substituting values
Distance covered by walking = 9/10 – 1/2
We know that LCM of 10 and 2 is 10
In order to convert fraction into equivalent fraction having 10 as denominator
Distance covered by walking = [(9 × 1)/ (10 × 1)] – [(1 × 5)/ (2 × 5)]
We get
Distance covered by walking = 9/10 – 5/10
By subtraction
Distance covered by walking = (9 – 5)/ 10 = 4/10 = 2/5 km
Hence, the distance covered by Ravish by walking is 2/5km.
FAQs on Ex-6.9, Fractions, Class 6, Maths RD Sharma Solutions - RD Sharma Solutions for Class 6 Mathematics
| 1. What are fractions and how are they represented? |  |
| 2. How do you add fractions with the same denominator? |  |
| 3. How can you simplify fractions? |  |
| 4. How do you compare fractions with different denominators? |  |
| 5. Can fractions be converted into decimals? |  |





















