Ex-19.3, Geometrical Constructions, Class 6, Maths RD Sharma Solutions | RD Sharma Solutions for Class 6 Mathematics PDF Download
Q.1 Draw a line segment of length 8.6 cm. Bisect it and measure the length of each part.
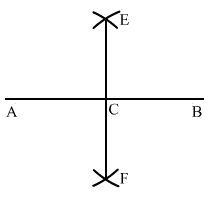
Sol.1 : Draw a line segment AB of length 8.6 cm.
With A as centre and radius more than half of AB, draw arcs on both sides of AB.
With the same radius and B as centre, draw arcs on the both sides of AB, cutting the previous two arcs at E and F.
Draw a line segment from E to F intersecting AB at C.
On measuring AC and BC, we get: AC = BC = 4.3 cm.
Q.2 Draw a line segment AB of length 5.8 cm. Draw the perpendicular bisector of this line segment.
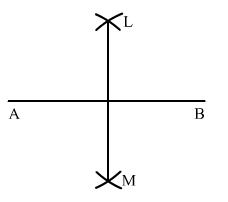
Sol.2 : Draw a line segment AB of length 5.8 cm using a ruler.
With A as centre and radius more than half of AB, draw arcs on both sides of AB.
With the same radius and B as centre, draw arcs on both sides of AB, intersecting the previous arcs at L and M.
Draw the line segment LM with L and M as end-points.
LM is the required perpendicular bisector of AB.
Q.3 Draw a circle with centre at point O and radius 5 cm. Draw its chord AB, draw the perpendicular bisector of line segment Ab. Does it pass through the centre of the circle?
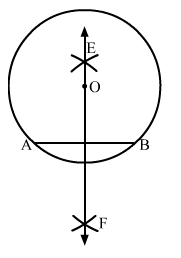
Sol.3 : Draw a point O. With O as centre and radius equal to 5 cm, draw a circle.
Take any two points A and B on the circumference of the circle and draw a line segment with A and B as its end points.
AB is the chord of the circle.
With A as centre and radius more than half of AB, draw arcs on both sides of AB.
With the same radius and B as a centre, draw arcs on both sides of AB, cutting the previous two arcs at E and F.
Draw a line passing through E and F.
Line EF passes through the centre of the circle O.
Q.4 Draw a circle with centre at point O. Draw its two chords AB and CD such that AB is not parallel to CD. Draw the perpendicular bisector of AB and CD. At what point do they intersect?
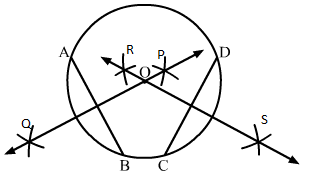
Sol.4 : Draw a circle with centre at 0. We draw two chords AB and CD as shown in the figure.
(i) With A as centre and radius more than half of AB, draw arcs on both sides of AB.
(ii) With the same radius and B as centre, draw arcs cutting the arcs of step (i) at P and Q.
(iii) Join P and Q.
(iv) With C as centre and radius more than half of CD, draw arcs on both sides of CD.
(v) With the same radius and D as centre, draw arcs cutting the arcs of step (iv) at R and S.
(vi) Join R and S.
We draw the line segments of perpendicular bisector of AB and CD.
We see that the perpendicular bisector of AB and CD meet at 0, the centre of the circle.
Q.5 Draw a line segment of length 10 cm and bisect it. Further bisect one of the equal parts and measure its length.
Sol.5 : Draw a line segment AB of length 10 cm and bisect it.
(i) With A as centre and radius more than half of AB, draw arcs on both sides of AB.
(ii) With the same radius and B as centre, draw arcs cutting the arcs of step (i) at P and Q, respectively.
(iii) Join P and Q. Line PQ intersects line AB at C.
(iv) With A as centre and radius more than half of AC, draw arcs on both sides of AB.
(v) With the same radius and C as centre, draw arcs cutting the arcs of step (iv) at R and S, respectively.
(vi) Join R and S.
Line RS intersects AC at D.
If we measure AD with the ruler, we have AD = 2.5 cm
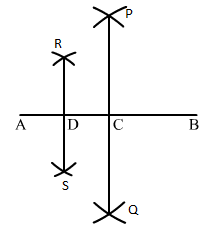
Q.6 Draw a line segment AB and bisect it. Bisect one of the equal parts to obtain a line segment of length 1/2(AB).
Sol.6 : Draw a line segment AB.
(i) With A as centre and radius more than half of AB , draw arcs on both sides of AB.
(ii) With the same radius and B as centre, draw arcs cutting the arcs drawn in step (i) at P and Q.
(iii) Join P and Q. PQ intersects AB at C.
(iv) With A as centre and radius more than half of AC, draw arcs on both sides of AC.
(v) With the same radius and C as centre, draw arcs cutting the arcs drawn in step (iv) at R and S.
(vi) Join R and S. RS intersects AB at D.
Now, AC and CB are equal.
Both are 1/2(AB). Again, divide AC at D.
So, AD and AC are of same length, i.e., 1/4(AB).
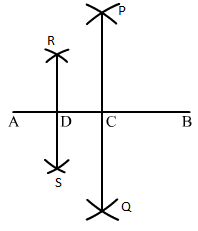
Q.7 Draw a line segment AB and by ruler and compasses, obtain a line segment of length 3/4(AB).
Sol.7 : Draw a line segment AB using the ruler.
(i) With A as centre and radius more than half of AB, draw arcs on both sides of AB.
(ii) With the same radius and B as centre, draw arcs cutting the arcs drawn in step (i) at P and Q.
(iii) Join P and Q. PQ intersects AB at C.
(i) With A as centre and radius more than half of AB, draw arcs on both sides of AC.
(ii) With the same radius and C as centre, draw arcs cutting the arcs drawn in step (iv) at R and S.
(iii) Join R and S. RS intersects AB at D.
Bisect AC again and mark the point of bisection as D.
So, we have: AD = 1/4(AB),
DC = 1/4 (AB) and CB = 1/2(AB)
Therefore, DB = 1/4 (AB) + 1/2(AB) = 3/4(AB)
Thus, DB is the required line segment of length 3/4(AB).
FAQs on Ex-19.3, Geometrical Constructions, Class 6, Maths RD Sharma Solutions - RD Sharma Solutions for Class 6 Mathematics
| 1. How can I construct a perpendicular bisector of a line segment? |  |
| 2. How can I construct an angle bisector? |  |
| 3. What is the construction for drawing a triangle when the lengths of its three sides are given? |  |
| 4. How can I construct a line parallel to a given line through a point not on the line? |  |
| 5. How can I construct a triangle given its base, one angle, and the difference of the other two sides? |  |
















