RD Sharma Solutions Ex-24.1, (Part - 2), Measures Of Central Tendency, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q 13. Explain, by taking a suitable example, how the arithmetic mean alters by
(i) adding a constant k to each term,
(ii) Subtracting a constant k from each term,
(iii) multiplying each term by a constant k and
(iv) dividing each term by non-zero constant k.
SOLUTION :
Let say numbers are 3 , 4 , 5
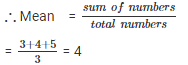
(i). Adding constant term k = 2 in each term.
New numbers are = 5 , 6 , 7
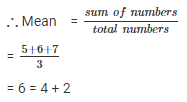
∴ new mean will be 2 more than the original mean.
(ii). Subtracting constant term k = 2 in each term.
New numbers are = 1 , 2 , 3

∴ new mean will be 2 less than the original mean.
(iii) . Multiplying by constant term k = 2 in each term.
New numbers are = 6 , 8 , 10
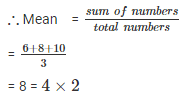
∴ new mean will be 2 times of the original mean.
(iv) . Divide the constant term k =2 in each term.
New numbers are = 1.5 , 2 , 2.5.

∴ new mean will be half of the original mean.
Q 14. The mean of marks scored by 100 students was found to be 40. Later on, it was discovered that a score of 53 was misread as 83. Find the correct mean.
SOLUTION :
Mean marks of 100 students = 40
Sum of marks of 100 students = 100×40
= 4000
Correct value = 53
Incorrect value = 83
Correct sum = 4000 – 83 + 53 = 3970
∴ correct mean = 3970/100 = 39.7
Q 15 . The traffic police recorded the speed (in km/hr) of 10 motorists as 47 , 53 , 49 , 60 , 39 , 42 , 55 , 57 , 52 , 48 . Later on, an error in recording instrument was found. Find the correct average speed of the motorists if the instrument is recorded 5 km/hr less in each case.
SOLUTION :
The speed of 10 motorists are 47 , 53 , 49 , 60 , 39 , 42 , 55 , 57 , 52 , 48 .
Later on it was discovered that the instrument recorded 5 km/hr less than in each case
∴ correct values are = 52 , 58 , 54 , 65 , 44 , 47 , 60 , 62 , 57 , 53.
∴ correct mean 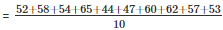
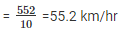
Q 16. The mean of five numbers is 27. If one number is excluded, their mean is 25. Find the excluded number.
SOLUTION :
The mean of five numbers is 27
The sum of five numbers = 5×27 = 135
If one number is excluded , the new mean is 25
∴Sum of 4 numbers = 4×25 = 100
∴ Excluded number = 135 – 100 = 35
Q 17. The mean weight per student in a group of 7 students is 55 kg. The individual weights of 6 of them (in kg) are 52, 54, 55, 53, 56 and 54. Find the weight of the seventh student.
SOLUTION :
The mean weight per student in a group of 7 students = 55 kg
Weight of 6 students (in kg) = 52 , 54 , 55 , 53 , 56 and 54
Let the weight of seventh student = x kg
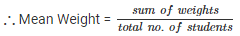
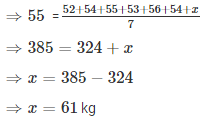
∴ weight of seventh student = 61 kg.
Q 18. The mean weight of 8 numbers is 15. If each number is multiplied by 2 , what will be the new mean?
SOLUTION :
We have ,
The mean weight of 8 numbers is 15
Then , the sum of 8 numbers = 8×15 = 120
If each number is multiplied by 2
Then , new mean = 120×2 = 240
∴ new mean = 240/8 = 30.
Q 19. The mean of 5 numbers is 18. If one number is excluded, their mean is 16. Find the excluded number.
SOLUTION :
The mean of 5 numbers is 18
Then , the sum of 5 numbers = 5×18 = 90
If one number is excluded
Then , the mean of 4 numbers = 16
∴ sum of 4 numbers = 4×16 = 64
Excluded number = 90 – 64 = 26.
Q 20. The mean of 200 items was 50. Later on, it was on discovered that the two items were misread as 92 and 8 instead of 192 and 88. Find the correct mean.
SOLUTION :
The mean of 200 items = 50
Then the sum of 200 items = 200×50 = 10,000
Correct values = 192 and 88.
Incorrect values = 92 and 8.
∴ correct sum = 10000 – 92 – 8 + 192 + 88 = 10180
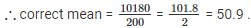
Q 21 . Find the values of n and 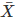 in each of the following cases :
in each of the following cases :
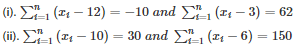
SOLUTION :
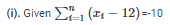
⇒ (x1−12)+(x2−12)+ ……… +(xn−12) = −10
⇒(x1+x2+x3+x4+x5+⋅⋅⋅+xn)−(12+12+12+12+⋅⋅⋅⋅+12)=−10
⇒ ∑ x−12n =−10⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅(1)
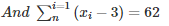
⇒ (x1−3)+(x2−3)+⋅⋅⋅⋅⋅+(xn−3) = 62
⇒ (x1+x2+⋅⋅⋅+xn)−(3+3+3+⋅⋅⋅+3) = 62
⇒ ∑x−3n = 62⋅⋅⋅⋅⋅⋅⋅⋅⋅(2)
By subtracting equation (1) from equation(2) , we get
∑x−3n−∑x+12n 62+10
⇒ 9n = 72
⇒ n = 72/9 = 8
Put value of n in equation (1)
∑x−12×8 = −10
⇒∑x−96 = −10
⇒∑x = 96−10 = 86
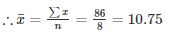
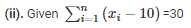
(x1−10)+(x2−10)+ ………… + (xn−10) = 30
⇒(x1+x2+x3+x4+x5+⋅⋅⋅+xn)−(10+10+10+10+⋅⋅⋅⋅+10) = 30
⇒ ∑x−10n = 30⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅(1)
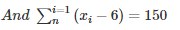
⇒(x1−6)+(x2−6)+⋅⋅⋅⋅⋅+(xn−6) = 150
⇒(x1+x2+⋅⋅⋅+xn)−(6+6+6+⋅⋅⋅+6) = 150
⇒∑x−6n = 150⋅⋅⋅⋅⋅⋅⋅⋅⋅(2)
By subtracting equation (1) from equation(2) , we get
∑x−6n−∑x+10n = 150−30
⇒ 4n = 120
⇒ n = 120/4 = 30
Put value of n in equation (1)
∑x−10×30 = 30
⇒ ∑x−300 = 30
⇒ ∑x=30+300 = 330
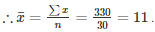
Q 22 . The sum of the deviations of a set of n values x1,x2,x3,⋅⋅⋅,xn measured from 15 and -3 are -90 and 54 respectively . Find the value of n and mean .
SOLUTION :
Given :
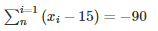
⇒ (x1−15)+(x2−15)+⋅⋅⋅⋅⋅+(xn−15) = −90
⇒ (x1+x2+⋅⋅⋅⋅+n)−(15+15+15+⋅⋅⋅⋅⋅⋅+15) =−90
⇒ ∑x−15n =−90⋅⋅⋅⋅⋅(1)
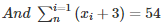
⇒ (x1+3)+(x2+3)+⋅⋅⋅⋅⋅+(xn+3) = 54
⇒ (x1+x2+⋅⋅⋅⋅+n)+(3+3+3+⋅⋅⋅⋅⋅⋅+3) = 54
⇒ ∑x+3n = 54⋅⋅⋅⋅⋅(2)
By subtracting equation (1) from equation(2) , we get
∑x+3n−∑x+15n = 54+90
⇒ 18n =144
⇒ n =144/18 = 8
Put value of n in equation(1)
∑x−15×8 = −90
∑x−120 = −90
∑x = 120−90 = 30
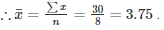
Q 23 . Find the sum of the deviations of the variate values 3 , 4 , 6 , 7 , 8 , 14 from their mean.
SOLUTION :
Values 3 , 4 , 6 , 7 , 8 , 14

= 7
∴ Sum of deviation of values from their mean
= (3−7)+(4−7)+(6−7)+(7−7)+(8−7)+(14−7)
= – 4 – 3 – 1 + 0 + 1 + 7
= – 8 + 8 = 0
Q 24 . If 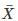 is the mean of the ten natural numbers x1,x2,x3,⋅⋅⋅,x10 show that
is the mean of the ten natural numbers x1,x2,x3,⋅⋅⋅,x10 show that
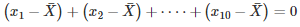
SOLUTION :
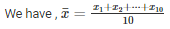
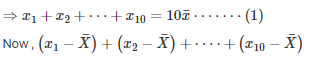
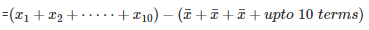
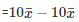 [Byequation(i)]
[Byequation(i)]
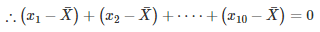
FAQs on RD Sharma Solutions Ex-24.1, (Part - 2), Measures Of Central Tendency, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are the measures of central tendency in statistics? |  |
| 2. How is the mean calculated? |  |
| 3. What is the median and how is it calculated? |  |
| 4. How is the mode determined in statistics? |  |
| 5. Can a data set have more than one mode? |  |

|
Explore Courses for Class 9 exam
|

|












