Ex - 4.2, Rational Numbers, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
Express each of the following as a rational number with positive denominator:
Answer 1:
Rational number with positive denominators:
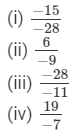
(i) Multiplying the number by −-1, we get:
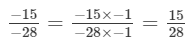
(ii) Multiplying the number by −-1, we get:
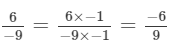
(iii) Multiplying the number by −-1, we get:
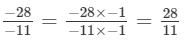
(iv) Multiplying the number by −-1, we get:
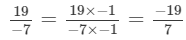
Question 2:
Express 3/5 as a rational number with numerator:
(i) 6
(ii) −15
(iii) 21
(iv) −27
Answer 2:
Rational number with numerator:
(i) 6 is:
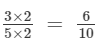
(multiplying numerator and denominator by 2 )
(ii)
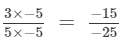
(multiplying numerator and denominator by -5)
(iii)
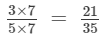
(multiplying numerator and denominator by 7)
(iv)
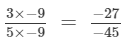
(multiplying numerator and denominator by -9)
Question 3:
Express 5757 as a rational number with denominator:
(i) −14
(ii) 70
(iii) −28
(iv) −84
Answer 3:
5/7 as a rational number with denominator:
(i) −14 is:
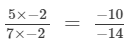 (multiplying numerator and denominator by -2)
(multiplying numerator and denominator by -2)
(ii) 70 is :
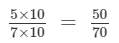 (multiplying numerator and denominator by 10)
(multiplying numerator and denominator by 10)
(iii) −28 is:
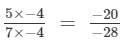 (multiplying numerator and denominator by -4)
(multiplying numerator and denominator by -4)
(iv) −84 is:
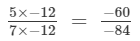 (multiplying numerator and denominator by -12)
(multiplying numerator and denominator by -12)
Question 4:
Express 3/4 as a rational number with denominator:
(i) 20
(ii) 36
(iii) 44
(iv) −80
Answer 4:
3/4 as rational number with denominator:
(i)
20 is:
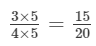 (multiplying numerator and denominator by 5)
(multiplying numerator and denominator by 5)
(ii)
36 is:
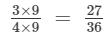 (multiplying numerator and denominator by 9)
(multiplying numerator and denominator by 9)
(iii)
44 is:
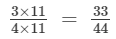 (multiplying numerator and denominator by 11)
(multiplying numerator and denominator by 11)
(iv)
−80 is:
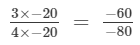 (multiplying numerator and denominator by -20)
(multiplying numerator and denominator by -20)
Question 5:
Express 2/5 as a rational number with numerator:
(i) −56
(ii) 154
(iii) −750
(iv) 500
Answer 5:
2/5 as a rational number with numerator:
(i)
−56 is:
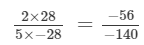 (multiplying numerator and denominator by -28)
(multiplying numerator and denominator by -28)
(ii)
154 is:
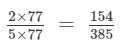 (multiplying numerator and denominator by 77)
(multiplying numerator and denominator by 77)
(iii)
−750 is:
 (multiplying numerator and denominator by -375)
(multiplying numerator and denominator by -375)
(iv)
500 is:
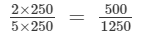 (multiplying numerator and denominator by 250)
(multiplying numerator and denominator by 250)
Question 6:
Express −192/108 as a rational number with numerator:
(i) 64
(ii) −16
(iii) 32
(iv) −48
Answer 6:
Rational number with numerator:
(i)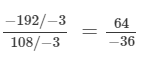 (Dividing the numerator and denomintor by −3)
(Dividing the numerator and denomintor by −3)
(ii)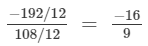 (Dividing the numerator and denomintor by 12)
(Dividing the numerator and denomintor by 12)
(iii) 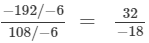 (Dividing the numerator and denomintor by −6)
(Dividing the numerator and denomintor by −6)
(iv) 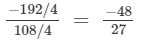 (Dividing the numerator and denomintor by 4)
(Dividing the numerator and denomintor by 4)
Question 7:
Express 168 / −294 as a rational number with denominator:
(i) 14
(ii) −7
(iii) −49
(iv) 1470
Answer 7:
Rational number with denominator:
(i) 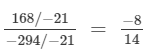 (Dividing the numerator and denomintor by −21)
(Dividing the numerator and denomintor by −21)
(ii) 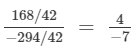 (Dividing the numerator and denomintor by 42)
(Dividing the numerator and denomintor by 42)
(iii) 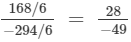 (Dividing the numerator and denomintor by 6)
(Dividing the numerator and denomintor by 6)
(iv) 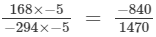 (Dividing the numerator and denomintor by −5)
(Dividing the numerator and denomintor by −5)
Question 8:
Write −14/42 in a form so that the numerator is equal to:
(i) −2
(ii) 7
(iii) 42
(iv) −70
Answer 8:
Rational number with numerator:
(i) 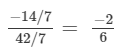 ( Dividing numerator and denominator by 7)
( Dividing numerator and denominator by 7)
(ii) 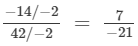 ( Dividing numerator and denominator by -2)
( Dividing numerator and denominator by -2)
(iii) 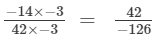 ( Dividing numerator and denominator by -3)
( Dividing numerator and denominator by -3)
(iv) 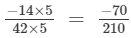 ( Dividing numerator and denominator by 5)
( Dividing numerator and denominator by 5)
Question 9:
Select those rational numbers which can be written as a rational number with numerator 6:
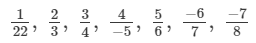
Answer 9:
Given rational numbers that can be written as a rational number with numerator 6 are:
1/22 (On multiplying by 6) = 6/132
2/3 (On multiplying by 3) = 6/9
3/4 (On multiplying by 2) = 6/8
−6/7 (On multiplying by −1) = 6/−7
Question 10:
Select those rational numbers which can be written as a rational number with denominator 4:
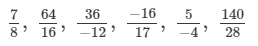
Answer 10:
Given rational numbers that can be written as a rational number with denominator 4 are:
7/8 (On dividing by 2) = 3.5/4
64/16 (On dividing by 4) =16/4
36/−12(On dividing by 3) =12/−4 = −12/4
−16/17 can't be expressed with a denominator 4.
5/−4(On multiplying by −1) =−5/4
140/28(On dividing by 7) =20/4
Question 11:
In each of the following, find an equivalent form of the rational number having a common denominator:
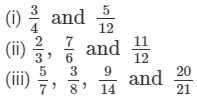
Answer 11:
Equivalent forms of the rational number having common denominator are:

(ii)
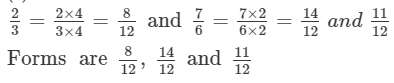
(iii)
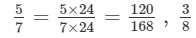
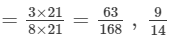
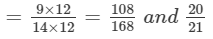
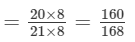
Forms are 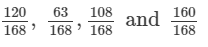
FAQs on Ex - 4.2, Rational Numbers, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are rational numbers? |  |
| 2. How can we determine if a number is rational or irrational? |  |
| 3. How can we simplify rational numbers? |  |
| 4. What is the difference between a proper fraction and an improper fraction? |  |
| 5. Can two rational numbers have the same decimal representation? |  |

|
Explore Courses for Class 7 exam
|

|

















