Ex - 4.5, Rational Numbers, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
Which of the following rational numbers are equal?
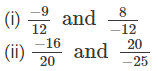
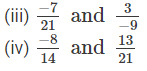
Answer 1:
i)
The standard form of 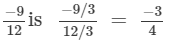
The standard form of 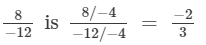
Since, the standard forms of two rational numbers are not same.Hence, they are not equal.
(ii)
Since, LCMof 20 and 25 is 100.Therefore making the denominators equal,
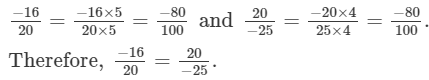
(iii)
Since, LCMof 21 and 9 is 63.Therefore making the denominators equal,
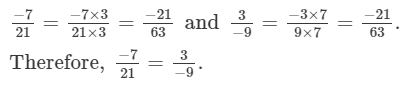
(iv)
Since, LCMof 14 and 21 is 42.Therefore making the denominators equal,
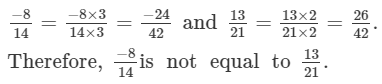
Question 2:
If each of the following pairs represents a pair of equivalent rational numbers, find the values of x:
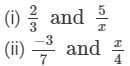
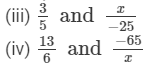
Answer 2:
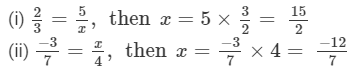
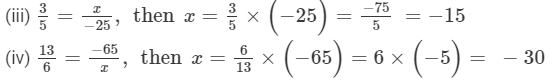
Question 3:
In each of the following, fill in the blanks so as to make the statement true:
(i) A number which can be expressed in the form p/q, where p and q are integers and q is not equal to zero, is called a .....
(ii) If the integers p and q have no common divisor other than 1 and q is positive, then the rational number p/q is said to be in the ....
(iii) Two rational numbers are said to be equal, if they have the same .... form.
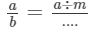
(v) If p and q are positive integers, then p/q is a ..... rational number and p/−q is a ..... rational number.
(vi) The standard form of −1 is ...
(vii) If p/q is a rational number, then q cannot be ....
(viii) Two rational numbers with different numerators are equal, if their numerators are in the same .... as their denominators.
Answer 3:
(i) rational number
(ii) standard rational number
(iii) standard form
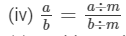
(v) positive rational number, negative rational number
(vi) −1/1
(vii) zero
(viii) ratio
Question 4:
In each of the following state if the statement is true (T) or false (F):
(i) The quotient of two integers is always an integer.
(ii) Every integer is a rational number.
(iii) Every rational number is an integer.
(iv) Every fraction is a rational number.
(v) Every rational number is a fraction
(vi) If a/b is a rational number and m any integer, then 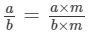
(vii) Two rational numbers with different numerators cannot be equal.
(viii) 8 can be written as a rational number with any integer as denominator.
(ix) 8 can be written as a rational number with any integer as numerator.
(x) 2/3 is equal to 4/6.
Answer 4:
(i) False; not necessary
(ii) True; every integer can be expressed in the form of p/q, where q is not zero.
(iii) False; not necessary
(iv) True; every fraction can be expressed in the form of p/q, where q is not zero.
(v) False; not necessary
(vi) True
(vii) False; they can be equal, when simplified further.
(viii) False
(ix) False
(x) True; in the standard form, they are equal.
FAQs on Ex - 4.5, Rational Numbers, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are rational numbers? |  |
| 2. How do you add two rational numbers? |  |
| 3. How do you multiply two rational numbers? |  |
| 4. Can a rational number be negative? |  |
| 5. How do you compare two rational numbers? |  |

|
Explore Courses for Class 7 exam
|

|

















