Ex - 4.6, Rational Numbers, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
Draw the number line and represent the following rational numbers on it:
(i) 2/3
(ii) 3/4
(iii) 3/8
(vi) −5/8
(v) −3/16
(vi) −7/3
(vii) 22/−7
(viii) −31/3
Answer 1:
(i)
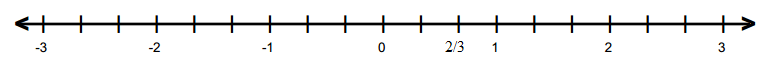
(ii)
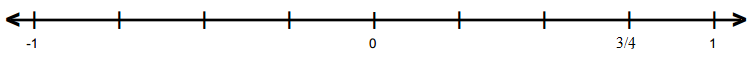
(iii)
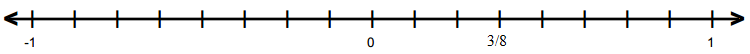
(iv)
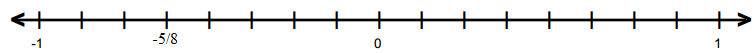
(v)
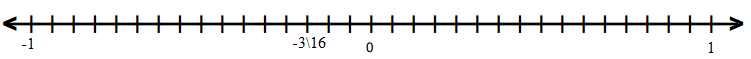
(vi)
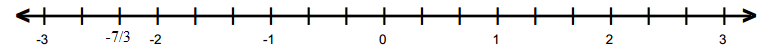
(vii) 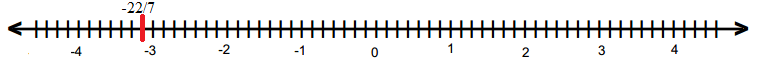
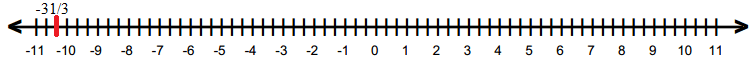
Question 2:
Which of the two rational numbers in each of the following pairs of rational numbers is greater?
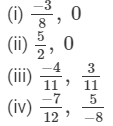

Answer 2:
(i) We know that every positive rational number is greater than zero and every negative rational number is smaller than zero. Thus,
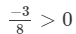
(ii) 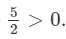 Because every positive rational number is greater than zero and every negative rational number is smaller than zero.
Because every positive rational number is greater than zero and every negative rational number is smaller than zero.
(iii) 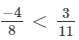 Because every positive rational number is greater than zero and every negative rational number is smaller than zero.
Because every positive rational number is greater than zero and every negative rational number is smaller than zero.
(iv)
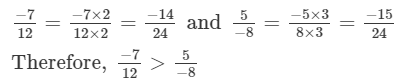
(v)
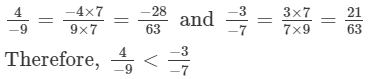
(vi)
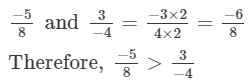
(vii)
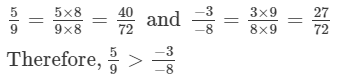
(viii)
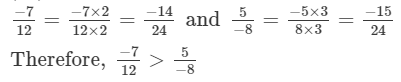
Question 3:
Which of the two rational numbers in each of the following pairs of rational numbers is smaller?
Answer 3:
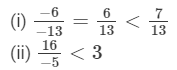
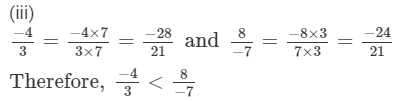
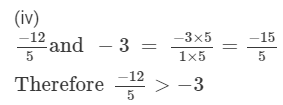
Question 4:
Fill in the blanks by the correct symbol out of >, =, or <:
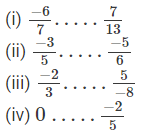
Answer 4:
(i) Because every positive number is greater than a negative number, −6/7 < 7/13
(ii) On multiplying −3/5 by 6/6, we get −18/30.
Because 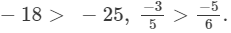
(iii) On multiplying −2/3 by 8/8, we get −16/24.
On multiplying 5/−8 by 3/3, we get 15/−24 = −15/24.
Because 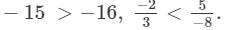
(iv) Because every positive number is greater than a negative number, 0>−2/5.
Question 5:
Arrange the following rational numbers in ascending order:
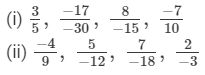
Answer 5:
(i) Ascending order:
Since, LCMof 5, −30, −15, 10 is 30.
Multiplying the numerators and denominators to get the denominator equal to the LCM,
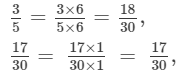
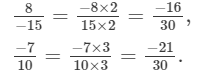
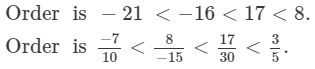
(ii)
Since, LCMof 9, −12, −18, 3 is 36.
Multiplying the numerators and denominators to get the denominator equal to the LCM,
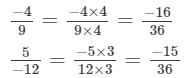
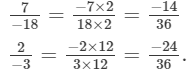
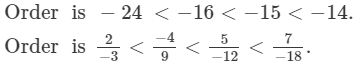
Question 6:
Arrange the following rational numbers in descending order:
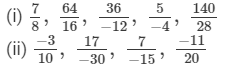
Answer 6:
We have to arrange them in descending order.
(i)
Since, LCMof 8, 16, −12, −4, 28 is 336.
Multiplying the numerators and denominators, to get the denominator equal to the LCM,
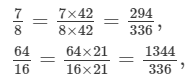
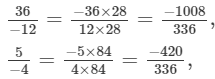
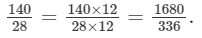
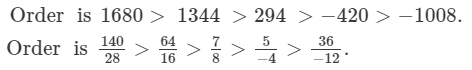
(ii)
Since, LCMof 10, −30, −15, 20 is 60.
Multiplying the numerators and denominators, to get the denominator equal to the LCM,
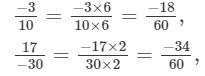
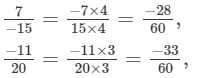
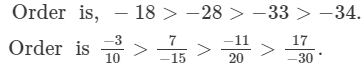
Question 7:
Which of the following statements are true:
(i) The rational number 29/23 lies to the left of zero on the number line.
(ii) The rational number −12/−17 lies to the left of zero on the number line.
(iii) The rational number 3/4 lies to the right of zero on the number line.
(iv) The rational numbers −12/−5 and −7/17 are on the opposite side of zero on the number line.
(v) The rational numbers −21/−5 and 7/−31 are on the opposite side of zero on the number line.
(vi) The rational number −3/−5 is one the right of −4/7 on the number line.
Answer 7:
(i) False; it lies to the right of zero because it is a positive number.
(ii) False; it lies to the right of zero because it is a positive number.
(iii) True
(iv) True; they are of opposite signs.
(v) False; they both are of same signs.
(v) True; they both are of opposite signs and positive number is greater than the negative number. Thus, it is on the right of the negative number.
FAQs on Ex - 4.6, Rational Numbers, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are rational numbers? |  |
| 2. How do you represent rational numbers on a number line? |  |
| 3. How do you compare rational numbers? |  |
| 4. Can a rational number be a whole number or an integer? |  |
| 5. How do you perform operations (addition, subtraction, multiplication, division) with rational numbers? |  |





















