Ex - 9.2, Ratio And Proportion, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
Which ratio is larger in the following pairs?
(i) 3 : 4 or 9 : 16
(ii) 15 : 16 or 24 : 25
(iii) 4 : 7 or 5 : 8
(iv) 9 : 20 or 8 : 13
(v) 1 : 2 or 13 : 27
Answer 1:
(i) Writing the ratios as fractions, we have
3 : 4 = 3/4 and 9 : 16 = 9/16
Now, LCM of 4 and 16 = 16.
Making the denominator of each fraction = 16, we have
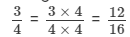 and the other fraction = 9/16
and the other fraction = 9/16
Of 12/16 and 9/16, clearly 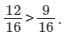
therefore, 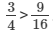
Writing the ratios as fractions, we have
15 : 16 = 15/16 and 24 : 25 = 24/25
Now, LCM of 16 and 25 = 400.
Making the denominator of each fraction = 400, we have
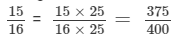 and the other fraction =
and the other fraction = 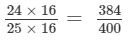
Clearly, 384 > 375. So, 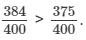
Therefore, 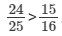
(iii) Writing the ratios as fractions, we have
4 : 7 = 4/7 and 5 : 8 = 5/8
Now, LCM of 7 and 8 = 56.
Making the denominator of each fraction = 56, we have
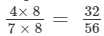 and the other fraction =
and the other fraction = 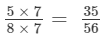
Clearly, 36 > 32. So,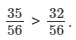
Therefore, 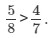
(iv) Writing the ratios as fractions, we have
9 : 20 = 9/20 and 8 : 13 = 8/13
Now, LCM of 20 and 13 = 260.
Making the denominator of each fraction = 260, we have
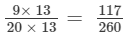 and the other fraction =
and the other fraction = 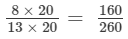
Clearly, 160 > 117. So,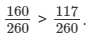
Therefore, 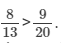
(v) Writing the ratios as fractions, we have
1 : 2 = 1/2 and 13 : 27 = 13/27
Now, LCM of 2 and 27 = 54.
Making the denominator of each fraction = 54, we have
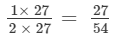 and the other fraction =
and the other fraction = 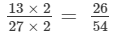
Clearly, 27 > 26. So, 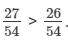
Therefore, 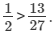
Question 2:
Give two equivalent ratios of 6 : 8.
Answer 2:
We have
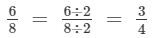
Therefore, 3 : 4 is an equivalent ratio of 6 : 8.
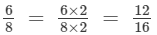
Hence, 3 : 4 and 12 : 16 are equivalent ratios of 6 : 8.
Question 3:
Fill in the following blanks: 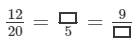
Answer 3:
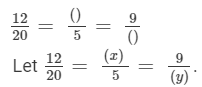
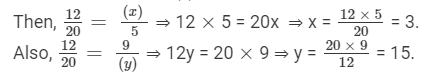
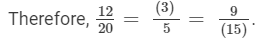
FAQs on Ex - 9.2, Ratio And Proportion, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What is the importance of understanding ratios and proportions in mathematics? |  |
| 2. How can I simplify a ratio to its simplest form? |  |
| 3. What are the key differences between a ratio and a proportion? |  |
| 4. How can ratios and proportions be applied in real-life situations? |  |
| 5. Can you provide an example of how ratios and proportions are used in business? |  |

|
Explore Courses for Class 7 exam
|

|

















