Ex - 9.3, Ratio And Proportion, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
Find which of the following are in proportion?
(i) 33, 44, 66, 88
(ii) 46, 69, 69, 46
(iii) 72, 84, 186, 217
Answer 1:
(i) We have
Product of extremes = 33 ×× 88 = 2904
Product of means = 44 ×× 66 = 2904
Therefore, the product of the extremes is equal to the product of the means.
Hence, 33, 44, 66, 88 are in proportion.
(ii) We have
Product of extremes = 46 ×× 46 = 2116
Product of means = 69 ×× 69 = 4761
Therefore, the product of the extremes is not equal to the product of the means.
Hence, 46, 69, 69, 46 are not in proportion.
(iii) We have
Product of extremes = 72 ×× 217 = 15624
Product of means = 84 ×× 186 = 15624
Therefore, the product of the extremes is equal to the product of the means.
Hence, 72, 84, 186, 217 are in proportion.
Question 2:
Find x in the following proportions:
(i) 16 : 18 = x : 96
(ii) x : 92 = 87 : 116
Answer 2:
(i) 16 : 18 = x : 96
⇒ 16, 18, x, and 96 are in proportion.
⇒ Product of extremes = Product of means
⇒ 16 × 96 = 18 × x
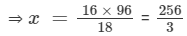
(ii) x : 92 = 87 : 116
⇒ x, 92, 87, and 116 are in proportion.
⇒ Product of extremes = Product of means
⇒ x × 116 = 87 × 92
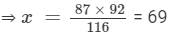
Question 3:
The ratio of the income to the expenditure of a family is 7 : 6. Find the savings if the income is Rs 1400.
Answer 3:
The ratio of the income of a family to its expenditure = 7 : 6.
Let us assume that the income and expenditure of the family are '7x' and '6x', respectively.
But the income = Rs. 1400.
Therefore, 7x = 1400
x = 1400/7 = 200
The expenditure = 6x = 6 × 200 = Rs. 1200.
Now, savings = Income - expenditure = Rs. (1400 - 1200) = Rs. 200.
Question 4:
The scale of a map is 1 : 4000000. What is the actual distance between the two towns if they are 5 cm apart on the map?
Answer 4:
The scale of the map = 1 : 4000000.
This means that 1 unit of distance on the map is equal to 4000000 units of the actual distance.
So, let us assume that the actual distance between the towns = 'x' cm.
Now, it is given that
1 : 4000000 = 5 : x
Hence, 1, 4000000, 5 and x are in proportion.
Therefore, product of extremes = product of means
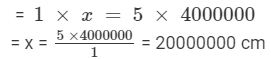
Since 1 km = 1000 m =1000××1 m =1000××100 cm = 100000 cm (1 m =100 cm),
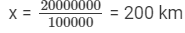
Question 5:
The ratio of income of a person to his savings is 10 : 1. If his savings of one year are Rs 6000, what is his income per month?
Answer 5:
Savings in one year = Rs. 6000
So, savings per month = 6000/12 = Rs. 500.
Let the income per month be Rs 'x'.
Then, x : 500 = 10 : 1.
So, x, 500, 10 and 1 are in proportion.
Product of extremes = Product of means
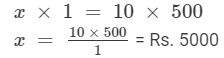
Question 6:
An electric pole casts a shadow of length 20 metres at a time when a tree 6 metres high casts a shadow of length 8 metres. Find the height of the pole.
Answer 6:
Length of the shadow of the electric pole = 20 m
Length of the shadow of the tree = 8 m
Height of the tree = 6 m
Now, let us assume that the height of the pole is 'x' m.
Height of the electric pole : length of the shadow of the electric pole = Height of the tree : length of the shadow of the tree
x : 20 = 6 : 8
Thus, x, 20, 6 and 8 are in proportion.
Product of extremes = Product of means
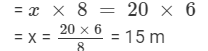
FAQs on Ex - 9.3, Ratio And Proportion, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What is the importance of studying ratio and proportion in mathematics? |  |
| 2. How do you find the ratio between two quantities? |  |
| 3. What are the properties of ratios and proportions? |  |
| 4. How are ratios and proportions used in real-life situations? |  |
| 5. Can you provide an example of solving a proportion? |  |

|
Explore Courses for Class 7 exam
|

|

















