RD Sharma Solutions (Part - 1) - Ex-20.3, Mensuration - I, Class 7, Math | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
Find the area of a parallogram with base 8 cm and altitude 4.5 cm.
Answer 1:
We have,
Base = 8 cm and altitude = 4.5 cm
Thus,
Area of the parallelogram = Base x Altitude
= 8 cm x 4.5 cm
= 36 cm
Question 2:
Find the area in square metres of the parallelogram whose base and altitudes are as under:
(i) Base = 15 dm, altitude = 6.4 dm
(ii) Base = 1 m 40 cm, altitude = 60 cm
Answer 2:
We have,
(i) Base = 15 dm = (15 x 10) cm = 150 cm = 1.5 m [Since 100 cm = 1 m]
Altitude = 6.4 dm = (6.4 x 10) cm = 64 cm = 0.64 m
Thus,
Area of the parallelogram = Base x Altitude
= 1.5 m x 0.64 m
= 0.96 m2
(ii) Base = 1 m 40 cm = 1.4 m [Since 100 cm = 1 m]
Altitude = 60 cm = 0.6 m
Thus,
Area of the parallelogram = Base x Altitude
= 1.4 m x 0.6 m
= 0.84 m2
Question 3:
Find the altitude of a parallelogram whose area is 54 dm2 and base is 12 dm.
Answer 3:
We have,
Area of the given parallelogram = 54 dm2
Base of the given parallelogram = 12 dm
∴ Altitude of the given parallelogram = Area/Base=54/12dm = 4.5 dm
Question 4:
The area of a rhombus is 28 m2. If its perimeter be 28 m, find its altitude.
Answer 4:
We have,
Perimeter of a rhombus = 28 m
∴ 4(Side) = 28 m [Since perimeter = 4(Side)]
⇒ Side = 28 m/4 =7 m
Now,
Area of the rhombus = 28 m2
⇒ (Side x Altitude) = 28 m2
⇒ (7 m x Altitude) = 28 m2
⇒ Altitude = 28 m2/ 7m =4 m
Question 5:
In Fig. 20, ABCD is a parallelogram, DL ⊥ AB and DM ⊥ BC. If AB = 18 cm, BC = 12 cm and DM = 9.3 cm, find DL.
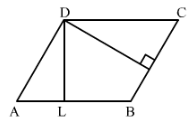
Answer 5:
We have,
Taking BC as the base,
BC = 12 cm and altitude DM = 9.3 cm
∴ Area of parallelogram ABCD = Base x Altitude
= (12 cm x 9.3 cm) = 111.6 cm2 ......... (i)
Now,
Taking AB as the base, we have,
Area of the parallelogram ABCD = Base x Altitude = (18 cm x DL).................(ii)
From (i) and (ii), we have
18 cm x DL = 111.6 cm2
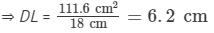
Question 6:
The longer side of a parallelogram is 54 cm and the corresponding altitude is 16 cm. If the altitude corresponding to the shorter side is 24 cm, find the length of the shorter side.
Answer 6:
We have,
ABCD is a parallelogram with the longer side AB = 54 cm and corresponding altitude AE = 16 cm.
The shorter side is BC and the corresponding altitude is CF = 24 cm.
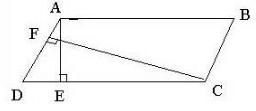
Area of a parallelogram = base × height.We have two altitudes and two corresponding bases. So,
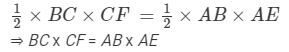
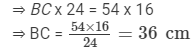
Hence, the length of the shorter side BC = AD = 36 cm.
Question 7:
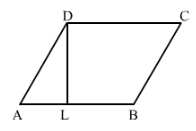
In Fig. 21, ABCD is a parallelogram, DL ⊥ AB. If AB = 20 cm, AD = 13 cm and area of the parallelogram is 100 cm2, find AL.
Answer 7:
We have,
ABCD is a parallelogram with base AB = 20 cm and corresponding altitude DL.
It is given that the area of the parallelogram ABCD = 100 cm2
Now,
Area of a parallelogram = Base x Height
100 cm2 = AB x DL
100 cm2 = 20 cm x DL

Again by Pythagoras theorem, we have,
(AD)2 = (AL)2 + (DL)2
⇒ (13)2 = (AL)2 + (5)2
⇒ (AL)2 = (13)2 - (5)2
= 169 − 25 = 144
⇒ (AL)2 = (12)2
⇒ AL = 12 cm
Hence. length of AL is 12 cm.
Question 8:
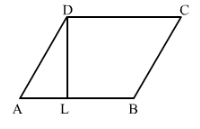
In Fig. 21, if AB = 35 cm, AD = 20 cm and area of the parallelogram is 560 cm2, find LB.
Answer 8:
We have,
ABCD is a parallelogram with base AB = 35 cm and corresponding altitude DL. The adjacent side of the parallelogram AD = 20 cm.
It is given that the area of the parallelogram ABCD = 560 cm2
Now,
Area of the parallelogram = Base x Height
560 cm2 = AB x DL
560 cm2 = 35 cm x DL

Again by Pythagoras theorem, we have,
(AD)2 = (AL)2 + (DL)2
⇒ (20)2 = (AL)2 + (16)2
⇒ (AL)2 = (20)2 − (16)2
= 400 − 256 = 144
⇒ (AL)2 = (12)2
⇒ AL = 12 cm
From the figure,
AB = AL + LB
35 cm = 12 cm + LB
∴ LB = 35 cm − 12 cm
= 23 cm
Hence, length of LB is 23 cm.
Question 9:
The adjacent sides of a parallelogram are 10 m and 8 m. If the distance between the longer sides is 4 m, find the distance between the shorter sides.
Answer 9:
We have,
ABCD is a parallelogram with side AB = 10 m and corresponding altitude AE = 4 m.
The adjacent side AD = 8 m and the corresponding altitude is CF.

Area of a parallelogram = Base × Height
We have two altitudes and two corresponding bases. So,
AD x CF = AB x AE
⇒ 8 m x CF = 10 m x 4 m
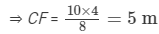
Hence, the distance between the shorter sides is 5 m.
Question 10:
The base of a parallelogram is twice its height. If the area of the parallelogram is 512 cm2, find the base and height.
Answer 10:
Let the height of the parallelogram be x cm.
Then the base of the parallelogram is 2x cm.
It is given that the area of the parallelogram = 512 cm2
So,
Area of a parallelogram = Base x Height
512 cm2 = 2x x x
512 cm2 = 2x2
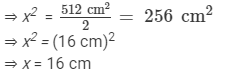
Hence, base = 2x = 2 x 16 = 32 cm and height = x = 16 cm.
FAQs on RD Sharma Solutions (Part - 1) - Ex-20.3, Mensuration - I, Class 7, Math - RD Sharma Solutions for Class 7 Mathematics
| 1. What are the formulas for calculating the surface area of different 3D shapes? |  |
| 2. How do I calculate the volume of a sphere? |  |
| 3. What is the difference between surface area and volume? |  |
| 4. How can I find the lateral surface area of a cone? |  |
| 5. Can you provide an example of calculating the volume of a cuboid? |  |

|
Explore Courses for Class 7 exam
|

|

















