RD Sharma Solutions (Part - 1) - Ex-20.4, Mensuration - I, Class 7, Math | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
Find the area in square centimetres of a triangle whose base and altitude are as under:
(i) base = 18 cm, altitude = 3.5 cm
(ii) base = 8 dm, altitude = 15 cm
Answer 1:
We know that the area of a triangle = 1/2×Base×Height
(i) Here, base = 18 cm and height = 3.5 cm
∴ Area of the triangle = (1/2×18×3.5)=31.5 cm2
(ii) Here, base = 8 dm = (8 x 10) cm = 80 cm [Since 1 dm = 10 cm]
and height = 3.5 cm
∴ Area of the triangle = (1/2×80×15)=600 cm2
Question 2:
Find the altitude of a triangle whose area is 42 cm2 and base is 12 cm.
Answer 2:
We have,
Altitude of a triangle = 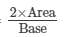
Here, base = 12 cm and area = 42 cm2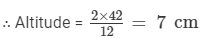
Question 3:
The area of a triangle is 50 cm2. If the altitude is 8 cm, what is its base?
Answer 3:
We have,
Base of a triangle = 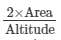
Here, altitude = 8 cm and area = 50 cm2
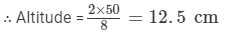
Question 4:
Find the area of a right angled triangle whose sides containing the right angle are of lengths 20.8 m and 14.7 m.
Answer 4:
In a right-angled triangle, the sides containing the right angles are of lengths 20.8 m and 14.7 m.
Let the base be 20.8 m and the height be 14.7 m.
Then,
Area of a triangle
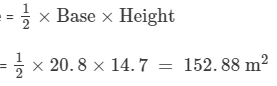
Question 5:
The area of a triangle, whose base and the corresponding altitude are 15 cm and 7 cm, is equal to area of a right triangle whose one of the sides containing the right angle is 10.5 cm. Find the other side of this triangle.
Answer 5:
For the first triangle, we have,
Base = 15 cm and altitude = 7 cm
Thus, area of a triangle = 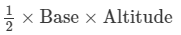
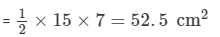
It is given that the area of the first triangle and the second triangle are equal.
Area of the second triangle = 52.5 cm2
One side of the second triangle = 10.5 cm
Therefore,
The other side of the second triangle = 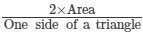
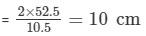
Hence, the other side of the second triangle will be 10 cm.
Question 6:
A rectangular field is 48 m long and 20 m wide. How many right triangular flower beds, whose sides containing the right angle measure 12 m and 5 m can be laid in this field?
Answer 6:
We have,
Length of the rectangular field = 48 m
Breadth of the rectangular field = 20 m
Area of the rectangular field = Length x Breadth = 48 m x 20 m = 960 m2
Area of one right triangular flower bed = 1/2×12 m×5 m = 30 m2
Therefore,
Required number of right triangular flower beds 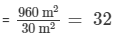
Question 7:
In Fig. 29, ABCD is a quadrilateral in which diagonal AC = 84 cm; DL ⊥ AC, BM ⊥ AC, DL = 16.5 cm and BM= 12 cm. Find the area of quadrilateral ABCD.
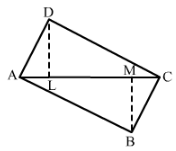
Answer 7:
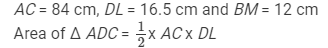
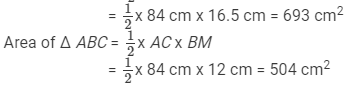
Hence,
Area of quadrilateral ABCD = Area of Δ ADC + Area of Δ ABC
= (693 + 504) cm2
= 1197 cm
Question 8:
Find the area of the quadrilateral ABCD given in Fig. 30. The diagonals AC and BD measure 48 m and 32 m respectively and are perpendicular to each other.
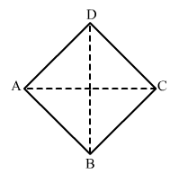
Answer 8:
We have,
Diagonal AC = 48 cm and diagonal BD = 32 m
∴ Area of a quadrilateral = 1/2 x Product of diagonals
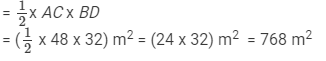
Question 9:
In Fig 31, ABCD is a rectangle with dimensions 32 m by 18 m. ADE is a triangle such that EF ⊥ AD and EF= 14 cm. Calculate the area of the shaded region.
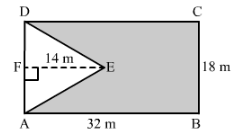
Answer 9:
We have,
Area of the rectangle = AB x BC
= 32 m x 18 m
= 576 m2
Area of the triangle = 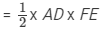
= 1/2x BC x FE [Since AD = BC]
= 1/2x 18 m x 14 m
= 9 m x 14 m = 126 m2
∴ Area of the shaded region = Area of the rectangle − Area of the triangle
=(576 − 126) m2
= 450 m
Question 10:
In Fig. 32, ABCD is a rectangle of length AB = 40 cm and breadth BC = 25 cm. If P, Q, R, S be the mid-points of the sides AB, BC, CD and DA respectively, find the area of the shaded region.
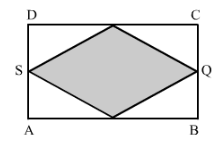
Answer 10:
We have,
Join points PR and SQ.
These two lines bisect each other at point O.
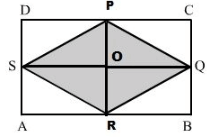
Here, AB = DC = SQ = 40 cm and AD = BC =RP = 25 cm
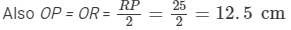
From the figure we observed that,
Area of Δ SPQ = Area of Δ SRQ
Hence, area of the shaded region 2 x (Area of Δ SPQ)

FAQs on RD Sharma Solutions (Part - 1) - Ex-20.4, Mensuration - I, Class 7, Math - RD Sharma Solutions for Class 7 Mathematics
| 1. What are the basic concepts of mensuration in Class 7 math? |  |
| 2. How is the area of a rectangle calculated in Class 7 math? |  |
| 3. What is the difference between area and perimeter? |  |
| 4. How can I calculate the volume of a cube in Class 7 math? |  |
| 5. What are some real-life applications of mensuration concepts learned in Class 7 math? |  |
















