RD Sharma Solutions (Part - 1) - Ex-14.2, Lines and Angles, Class 7, Math | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
In Fig., line n is a transversal to lines l and m. Identify the following:
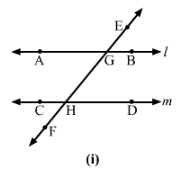
(i) Alternate and corresponding angles in Fig. (i).
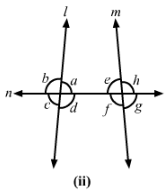
(ii) Angles alternate to ∠d and ∠g and angles corresponding to angles ∠f and ∠h in Fig. (ii).
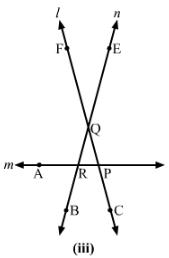
(iii) Angle alternate to ∠PQR, angle corresponding to ∠RQF and angle alternate to ∠PQE in Fig. (iii).
(iv) Pairs of interior and exterior angles on the same side of the transversal in Fig. (ii).
Answer 1:
(i) Figure (i)
Corresponding angles:
∠EGB and ∠GHD
∠HGB and ∠FHD
∠EGA and ∠GHC
∠AGH and ∠CHF
Alternate angles:
∠EGB and ∠CHF
∠HGB and ∠CHG
∠EGA and ∠FHD
∠AGH and ∠GHD
(ii) Figure (ii)
Alternate angle to ∠d is ∠e.
Alternate angle to ∠g is ∠b.
Also,
Corresponding angle to ∠f is ∠c.
Corresponding angle to ∠h is ∠a.
(iii) Figure (iii)
Angle alternate to ∠PQR is ∠QRA.
Angle corresponding to ∠RQF is ∠ARB.
Angle alternate to ∠POE is ∠ARB.
(iv) Figure (ii)
Pair of interior angles are
∠a and ∠e
∠d and ∠f
Pair of exterior angles are
∠b and ∠h
∠c and ∠g
Question 2:
In Fig., AB and CD are parallel lines intersected by a transversal PQ at L and M respectively. If ∠CMQ = 60°, find all other angles in the figure.
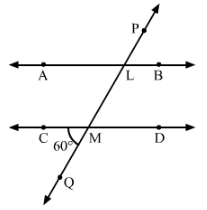
Answer 2:
∠ALM = ∠CMQ = 60°60° (Corresponding angles)
∠LMD = ∠CMQ = 60°60° (Vertically opposite angles)
∠ALM = ∠PLB = 60°60° (Vertically opposite angles)
Since
∠CMQ + ∠QMD = 180°180° (Linear pair)
∴ ∠QMD = 180°−60°=120°
∠QMD = ∠MLB = 120° (Corresponding angles)
∠QMD = ∠CML = 120° (Vertically opposite angles)
∠MLB = ∠ALP = 120° (Vertically opposite angles)
Question 3:
In Fig., AB and CD are parallel lines intersected by a transversal PQ at L and M respectively. If ∠LMD = 35° find ∠ALM and ∠PLA.
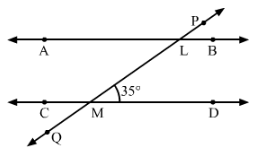
Answer 3:
In the given Fig., AB || CD.
∠ALM=∠LMD=35° (Alternate interior angles)
Since ∠PLA+∠ALM=180° (Linear pair)
∴∠PLA=180°−35°=145°
Question 4:
The line n is transversal to line l and m in Fig. Identify the angle alternate to ∠13, angle corresponding to ∠15, and angle alternate to ∠15.
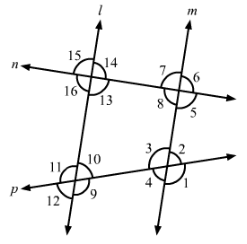
Answer 4:
In this given Fig., line l || m.
Here,
Alternate angle to ∠13 is ∠7.
Corresponding angle to ∠15 is ∠7.
Alternate angle to ∠15 is ∠5.
Question 5:
In Fig., line l || m and n is a transversal. If ∠1 = 40°, find all the angles and check that all corresponding angles and alternate angles are equal.
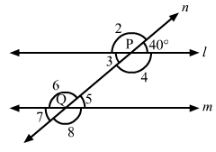
Answer 5:
In the given figure, l || m.
Here,
∠1+∠2=180° (Linear pair)
∴ ∠2=180°−∠1=180°- 40°=140°
∠5=∠1=40° (Corresponding angles)
∠3=∠1=40° (Vertically opposite angles)
∠7=∠3=40° (Corresponding angles)
∠7=∠5=40° (Vertically opposite angles)
Also,
∠2=∠6=140° (Corresponding angles)
∠2=∠4=140° (Vertically opposite angles)
∠4=∠8=140° (Corresponding angles)
∠8=∠6=40° (Vertically opposite angles)
Thus,
∠2=∠8, ∠3=∠5, ∠6=∠4, ∠1=∠7
Hence, alternate angles are equal.
Question 6:
In Fig., line l || m and a transversal n cuts them at P and Q respectively. If ∠1 = 75°, find all other angles
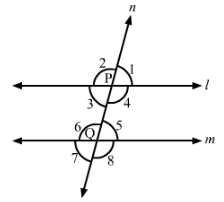
Answer 6:
In the given figure, l || m, n is a transversal line and ∠1 = 75°.
Thus, we have:
∠1+∠2=180° (Linear pair)
⇒∠2=180°−∠1=180°−75°=105°
∴∠1=∠5=75° (Corresponding angles)
∠1=∠3=75° (Vertically opposite angles)
∠5=∠7=75° (Vertically opposite angles)
Now,
∠2=∠6=105° (Corresponding angles)
∠6=∠8=105° (Vertically opposite angles)
∠2=∠4=105° (Vertically opposite angles)
Question 7:
In Fig., AB || CD and a transversal PQ cuts them at L and M respectively. If ∠QMD = 100°, find all other angles.
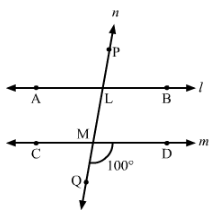
Answer 7:
In the given figure, AB || CD, PQ is a transversal line and ∠QMD = 100°.
Thus, we have:
∠DMQ + ∠QMC = 180° (Linear pair)
∴∠QMC=180°−∠DMQ=180°−100°=80°
Thus,
∠DMQ = ∠BLM = 100° (Corresponding angles)
∠DMQ = ∠CML = 100° (Vertically opposite angles)
∠BLM = ∠PLA = 100° (Vertically opposite angles)
Also,
∠CMQ = ∠ALM = 80° (Corresponding angles)
∠CMQ = ∠DML = 80° (Vertically opposite angles)
∠ALM = ∠PLB = 80° (Vertically opposite angles)
Question 8:
In Fig., l || m and p || q. Find the values of x, y, z, t.

Answer 8:
In the given figure, l || m and p || q.
Thus, we have:
∠z=80°∠z=80° (Vertically opposite angles)
∠z=∠t=80°∠z=∠t=80° (Corresponding angles)
∠z=∠y=80°∠z=∠y=80° (Corresponding angles)
∠x=∠y=80°∠x=∠y=80° (Corresponding angles)
Question 9:
In Fig., line l || m, ∠1 = 120° and ∠2 = 100°, find out ∠3 and ∠4.
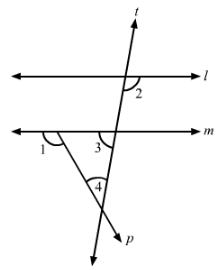
Answer 9:
In the given figure, ∠1 = 120° and ∠2 =100°.
Since l || m, so
∠2=∠5=100° (Alternate interior angles)
∠5+∠3=180° (Linear pair)
⇒∠3=180°−∠5=180°−100°=80°
Also,
∠1+∠6=180° (Linear pair)
⇒∠6=180°−∠1=180°−120°=60°
We know that the sum of all the angles of triangle is 180°.
∴∠6+∠3+∠4=180°
⇒60°+80°+∠4=180°
⇒140°+∠4=180°
⇒∠4=180°−140°=40°
Question 10:
In Fig., line l || m. Find the values of a, b, c, d. Give reasons.

Answer 10:
In the given figure, line l || m.
Thus, we have:
∠a=110° (Vertically opposite angles)
∠b=∠a=110° (Corresponding angles)
∠d=85° (Vertically opposite angles)
∠c=∠d=85° (Corresponding angles)
Question 11:
In Fig., AB || CD and ∠1 and ∠2 are in the ratio 3 : 2. Determine all angles from 1 to 8.
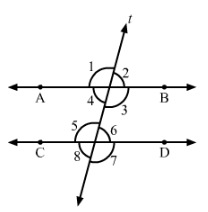
Answer 11:
In the given figure, AB || CD and t is a transversal line.
Now, let:
∠1=3x
∠2=2x
Thus, we have:
∠1+∠2=180° (Linear pair)
∴ 3x+2x=180°
⇒5x=180°
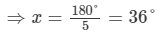
Thus,∠1=3×36°=108°
∠2=2×36°=72°
Now,
∠1=∠5=108° (Corresponding angles)
∠1=∠3=108° (Vertically opposite angles)
∠5=∠7=108° (Vertically opposite angles)
∠2=∠6=72° (Corresponding angles)
∠4=∠2=72° (Vertically opposite angles)
∠8=∠6=72° (Vertically opposite angles)
Question 12:
In Fig., l, m and n are parallel lines intersected by transversal p at X, Y and Z respectively. Find ∠1, ∠2 and ∠3.
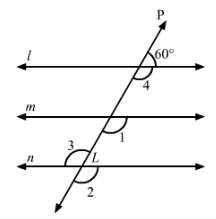
Answer 12:
In the given figure, l || m || n and p is a transversal line.
Thus, we have:
∠4+60°=180° (Linear pair)
⇒∠4=180°−60°=120°∠4=∠1=120° (Corresponding angles)
∠1=∠2=120° (Corresponding angles)
∠3=∠2=120° (Vertically opposite angles)
Thus,
∠1=∠2=∠3=120°
FAQs on RD Sharma Solutions (Part - 1) - Ex-14.2, Lines and Angles, Class 7, Math - RD Sharma Solutions for Class 7 Mathematics
| 1. What are the different types of angles in geometry? |  |
| 2. How do you identify alternate angles? |  |
| 3. What is the difference between supplementary and complementary angles? |  |
| 4. How do you find the sum of the interior angles of a polygon? |  |
| 5. How do you determine if two lines are parallel? |  |

|
Explore Courses for Class 7 exam
|

|

















