Ex-5.4 & Ex-5.5, Operations On Rational Numbers, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Ex-5.4
Q1. Divide:
Solution.
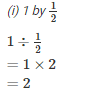
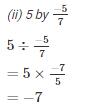
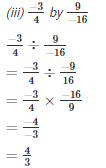
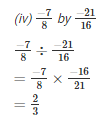
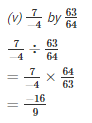
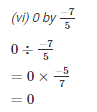
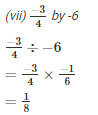
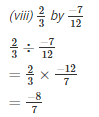
Q2. Find the value and express as a rational number in standard form:
Solution.
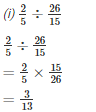
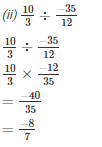
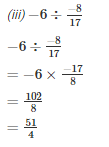
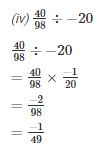
Q3. The product of two rational numbers is 15. If one of the numbers is -10, find the other.
Solution.
Let the number to be found be x
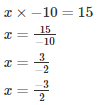
Hence the number is 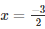
Q4. The product of two rational numbers is −8/9. If one of the numbers is −4/15, find the other.
Solution.
Let the number to be found be x
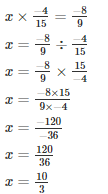
Hence the number is x = 10/3
Q5. By what number should we multiply −1/6 so that the product may be −23/9?
Solution.
Let the number to be found be x
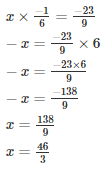
Hence the number is x = 46/3
Q6. By what number should we multiply −15/28 so that the product may be −5/7?
Solution.
Let the number to be found be x
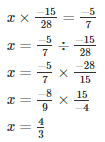
Hence the number is x = 4/3
Q7. By what number should we multiply −8/13 so that the product may be 24?
Solution.
Let the number to be found be x
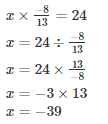
Hence the number is x=−39
Q8. By what number should −3/4 be multiplied in order to produce −2/3?
Solution.
Let the number to be found be x
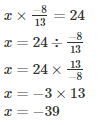
Hence the number is x = −39
Q9. Find (x + y)÷(x —y), if
Solution.
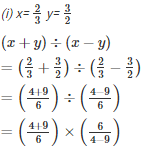
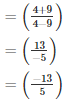
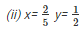
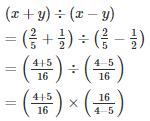
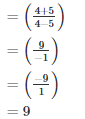
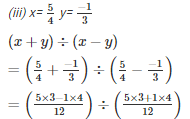
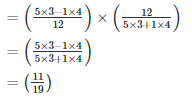
Q10. The cost of 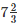 metres of rope is Rs.
metres of rope is Rs. 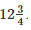 Find its cost per metre.
Find its cost per metre.
Solution.
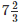 metres of rope cost= Rs
metres of rope cost= Rs 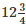
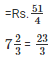
Cost per metre 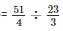
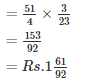
Q11. The cost of 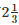 metres of cloth is Rs
metres of cloth is Rs 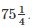 Find the cost of cloth per metre.
Find the cost of cloth per metre.
Solution.
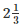 metres of rope cost =
metres of rope cost = 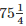
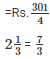
Cost per metre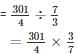
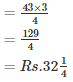
Q12. By what number should −33/16 be divided to get −11/4?
Solution.
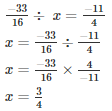
The number is x = 3/4
Q13. Divide the sum of −13/5 and 12/7 by the product of −31/7 and −1/2
Solution.
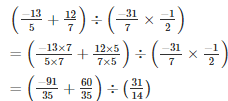
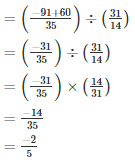
Q14. Divide the sum of 65/12 and 8/3 by their difference.
Solution.
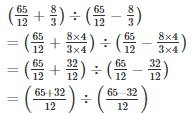
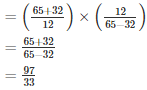
Q15. If 24 trousers of equal size can be prepared in 54 metres of cloth, what length of cloth is required for each trouser?
Solution.
Length of cloth required for each trouser 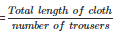
= 54/24
= 94metres
9/4mmetres of cloth is required to make each trouser
Ex-5.5
Q1. Find six rational numbers between −4/8 and 3/8
We know that
-4,-3,-2,-1,0,1,2,3
Therefore 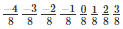
Hence 6 rational numbers between 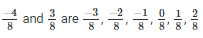
Q2. Find 10 rational numbers between 7/13 and −4/13
We know that
76543210-1-2-3-4
Therefore 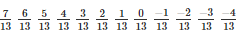
Hence the 10 rational numbers between 7/13 and −4/13 are
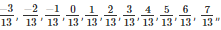
Q3. State true or false:
(i) Between any two distinct integers there is always an integer.
FALSE
(ii) Between any two distinct rational numbers there is always a rational number.
TRUE
(iii) Between any two distinct rational numbers there are infinitely many rational numbers.
TRUE
FAQs on Ex-5.4 & Ex-5.5, Operations On Rational Numbers, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are rational numbers? |  |
| 2. How do we perform addition and subtraction of rational numbers? |  |
| 3. Can we multiply and divide rational numbers? |  |
| 4. How do we simplify rational numbers? |  |
| 5. Can rational numbers be negative? |  |

|
Explore Courses for Class 7 exam
|

|

















