RD Sharma Solutions (Part - 2) - Ex-23.1, Data Handling II Central Values, Class 7, Math | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 14:
The percentage of marks obtained by students of a class in mathematics are:
64, 36, 47, 23, 0, 19, 81, 93, 72, 35, 3, 1. Find their mean.
Answer 14:
We have :
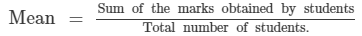

Question 15:
The numbers of children in 10 families of a locality are:
2, 4, 3, 4, 2, 3, 5, 1, 1, 5. Find the mean number of children per family.
Answer 15:
The mean number of children per family = 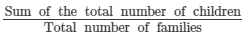
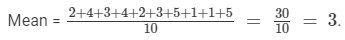
Thus, on an average there are 3 children per family in the locality.
Question 16:
The mean of marks scored by 100 students was found to be 40. Later on it was discovered that a score of 53 was misread as 83. Find the correct mean.
Answer 16:
We have:
n = The number of observations = 100, Mean = 40
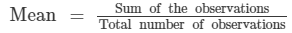
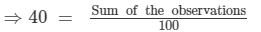
⇒ 40 ×100 = Sum of the observations
Thus, the incorrect sum of the observations = 40 x 100 = 4000.
Now,
The correct sum of the observations = Incorrect sum of the observations - Incorrect observation + Correct observation
⇒ The correct sum of the observations = 4000 - 83 + 53
⇒ The correct sum of the observations = 4000 - 30 = 3970
∴ 
Question 17:
The mean of five numbers is 27. If one number is excluded, their mean is 25. Find the excluded number.
Answer 17:
We have:

So, sum of the five numbers = 5 ×27 = 135.
Now,
The mean of four numbers = 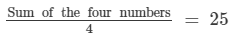
So, sum of the four numbers = 4 ×25 = 100.
Therefore, the excluded number = Sum of the five numbers - sum of the four numbers
⇒ The excluded number = 135 - 100 = 35.
Question 18:
The mean weight per student in a group of 7 students is 55 kg. The individual weights of 6 of them (in kg) are 52, 54, 55, 53, 56 and 54. Find the weight of the seventh student.
Answer 18:
We have:
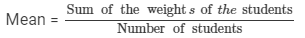
Let the weight of the seventh student be x kg.
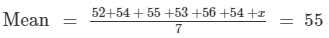
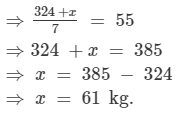
Thus, the weight of the seventh student is 61 kg.
Question 19:
The mean weight of 8 numbers is 15 kg. If each number is multiplied by 2, what will be the new mean?
Answer 19:
Let x1, x2, x3...x8 be the eight numbers whose mean is 15 kg. Then,
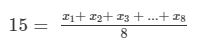
x1, x2, x3...x8 = 15 x 8
⇒ x1, x2, x3...x8 = 120
Let the new numbers be 2x1 , 2x2, 2x3, ...2x8. Let M be the arithmetic mean of the new numbers.
Then,
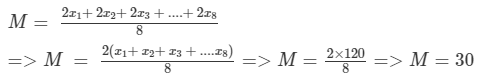
Question 20:
The mean of 5 numbers is 18. If one number is excluded, their mean is 16. Find the excluded number.
Answer 20:
Let x1,x2,x3,x4 & x5x1,x2,x3,x4 & x5 be five numbers whose mean is 18. Then,
18 = Sum of five numbers ÷ 5
∴ Sum of five numbers = 18 × 5 = 90.
Now, if one number is excluded, then their mean is 16.
So,
16= Sum of four numbers ÷ 4
∴ Sum of four numbers = 16 × 4 = 64.
The excluded number = Sum of the five observations - Sum of the four observations
∴ The excluded number = 90 - 64
∴ The excluded number = 26.
Question 21:
The mean of 200 items was 50. Later on, it was discovered that the two items were misread as 92 and 8 instead of 192 and 88. Find the correct mean.
Answer 21:
n = Number of observations = 200

⇒Sum of the observations = 50 × 200 = 10,000
Thus, the incorrect sum of the observations = 50 x 200
Now,
The correct sum of the observations = Incorrect sum of the observations - Incorrect observations + Correct observations
⇒Correct sum of the observations = 10,000 - (92+ 8) + (192 + 88)
⇒ Correct sum of the observations = 10,000 - 100 + 280
⇒ Correct sum of the observations = 9900 +280
⇒ Correct sum of the observations = 10180.

Question 22:
The mean of 5 numbers is 27. If one more number is included, then the mean is 25. Find the included number.
Answer 22:
We have:
Mean = Sum of five numbers ÷ 5
⇒ Sum of the five numbers = 27 x 5 = 135.
Now, New mean = 25
25 = Sum of six numbers ÷÷ 6
⇒ Sum of the six numbers = 25 x 6 = 150.
The included number = Sum of the six numbers - Sum of the five numbers
⇒The included number = 150 - 135
⇒The included number = 15.
Question 23:
The mean of 75 numbers is 35. If each number is multiplied by 4, find the new mean.
Answer 23:
Let x1, x2, x3, ... x75 be 75 numbers with their mean equal to 35. Then,
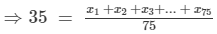
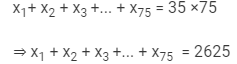
The new numbers are 4x1, 4x2, 4x3, ...4x75. Let M be the arithmetic mean of the new numbers. Then,
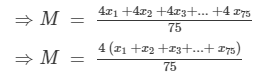
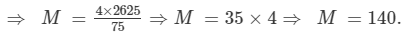
FAQs on RD Sharma Solutions (Part - 2) - Ex-23.1, Data Handling II Central Values, Class 7, Math - RD Sharma Solutions for Class 7 Mathematics
| 1. What are the different measures of central tendency in data handling? |  |
| 2. How is the mean calculated in data handling? |  |
| 3. What is the significance of median in data handling? |  |
| 4. How is the mode determined in data handling? |  |
| 5. When should we use the mean, median, or mode in data handling? |  |

|
Explore Courses for Class 7 exam
|

|

















