Ex-6.2, Exponents, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Q1. Using laws of exponents, simplify and write the answer in exponential form
(i) 23×24×25
(ii) 512÷53
(iii) (72)3
(iv) (32)5÷34
(v) 37×27
(vi) (521÷513)×57
Sol:
(i) 23×24×25
We know that, am+an+ap = am+n+p
So, 23×24×25 = 23+4+5
= 212
(ii) 512÷53
We know that, am÷an = am−n
So, 512÷53 = 512−3
= 59
(iii) (72)3
We know that, (am)n=amn
So, (72)3 = 7(2)(3)
= 76
(iv) (32)5÷34
We know that, am÷an = am−n and (am)n = amn
So, (32)5÷34 = 310÷34
= 310−4
= 36
(v) 37×27
We know that, (am×bm)=(a×b)m
So, 37×27 = (3×2)7
= 67
(vi) (521÷513)×57
We know that, am÷an=am−n and(am×an)=(a)m+n
So, (521÷513)×57 = (521−13)×57
= (58)×57
= 58+7
= 515
Q2. Simplify and express each of the following in exponential form
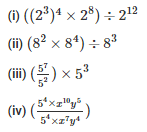
Sol:
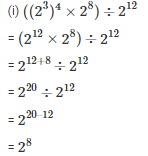
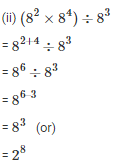
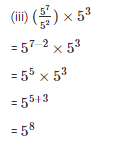
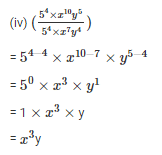
Q3. Simplify and express each of the following in exponential form
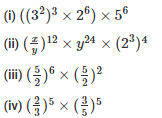
Sol:
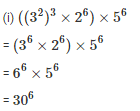
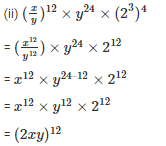
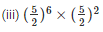
We know that, 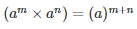
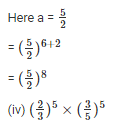
We know that, 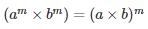
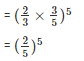
Q4. Write 9 ×9 ×9 ×9 ×9 in exponential form with base 3
Sol:
9 ×9 ×9 ×9 ×9 = (9)5 = (32)5
= 310
Q5. Simplify and write each of the following in exponential form
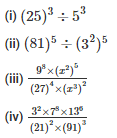
Sol:
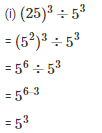
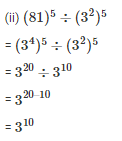
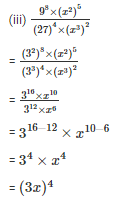
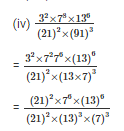
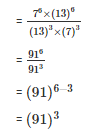
Q6. Simplify
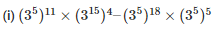
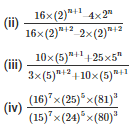
Sol:
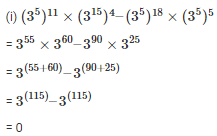
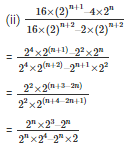
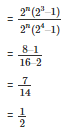
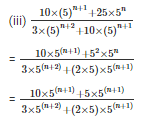
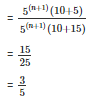
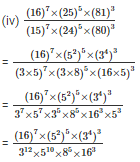
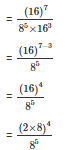
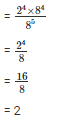
Q7. Find the values of n in each of the following
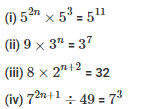
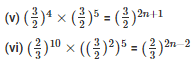
Sol:
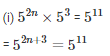
Equating the powers
= 2n + 3 = 11
= 2n = 11- 3
= 2n = 8
= n = 4
(ii) 9×3n = 37
= 32×3n = 37
= 32+n = 37
Equating the powers
= 2 + n = 7
= n = 7 – 2
= n = 5
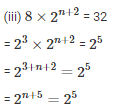
Equating the powers
= n + 5 = 5
= n = 0
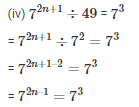
Equating the powers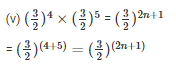
Equating the powers
= 4 + 5 = 2n + 1
= 2n + 1 = 9
= 2n = 8
= n = 4
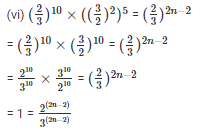
= 3(2n – 2) =2(2n – 2)
= 6n – 6 = 4n – 4
= 6n – 4n = 6 – 4
= 2n = 2
= n = 1
Q8.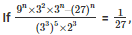 find the value of n
find the value of n
Sol:
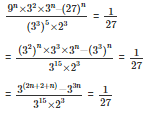
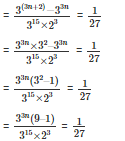
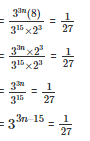
On equating the coefficient
3n – 15 = -3
3n = -3 + 15
3n = 12
n = 4
FAQs on Ex-6.2, Exponents, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are exponents in mathematics? |  |
| 2. How do exponents work with negative numbers? |  |
| 3. What is the meaning of a zero exponent? |  |
| 4. How do exponents work with fractions? |  |
| 5. What is the difference between exponents and logarithms? |  |

|
Explore Courses for Class 7 exam
|

|


















