Ex-15.2, (Part - 2), Properties Of Triangles, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Q15.Find x,y,z(whichever is required) from the figures given below


Solution.
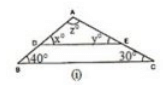
(i) In ΔABC and ΔADE we have :
∠ADE = ∠ABC (corresponding angles)
x = 40∘
∠AED = ∠ACB (corresponding angles)
y = 30∘
We know that the sum of all the three angles of a triangle is equal to 180∘
x +y +z = 180∘ (Angles of A ADE)
Which means : 40∘ +30∘ + z = 180∘
z = 180∘−70∘
z = 110∘
Therefore, we can conclude that the three angles of the given triangle are 40∘, 30∘ and 110∘.
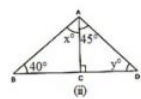
(ii) We can see that in ΔADC, ∠ADC is equal to 90∘.
(ΔADC is a right triangle)
We also know that the sum of all the angles of a triangle is equal to 180∘.
Which means : 45∘+ 90∘ +y = 180∘ (Sum of the angles of ΔADC)
135∘ + y = 180∘
y = 180∘ – 135∘.
y = 45∘.
We can also say that in ΔABC, ∠ABC+∠ACB+∠BAC is equal to 180∘.
(Sum of the angles of A ABC)
40∘ + y + (x + 45∘) = 180∘
40∘ + 45∘ + x + 45∘ = 180∘ (y = 45∘)
x = 180∘ –130∘
x = 50∘
Therefore, we can say that the required angles are 45∘ and 50∘.
(iii) We know that the sum of all the angles of a triangle is equal to 180∘.
Therefore, for ΔABD:
∠ABD+∠ADB+∠BAD = 180∘ (Sum of the angles of ΔABD)
50∘ + x + 50∘ = 180∘
100∘ +x = 180∘
x = 180∘ –100∘
x = 80∘
For ΔABC:
∠ABC+∠ACB+∠BAC = 180∘ (Sum of the angles of ΔABC)
50∘ + z + (50∘ + 30∘) = 180∘
50∘ + z + 50∘ + 30∘ = 180∘
z = 180∘ – 130∘
z = 50∘
Using the same argument for ΔADC:
∠ADC+∠ACD+∠DAC = 180∘ (Sum of the angles of ΔADC)
y +z +30∘ =180∘
y + 50∘ + 30∘ =180∘ (z = 50∘)
y = 180∘ – 80∘
y = 100∘
Therefore, we can conclude that the required angles are 80∘, 50∘ and 100∘.
(iv) In ΔABC and ΔADE we have :
∠ADE = ∠ABC (Corresponding angles)
y = 50∘
Also, ∠AED =∠ACB (Corresponding angles)
z = 40∘
We know that the sum of all the three angles of a triangle is equal to 180∘.
Which means : x+50∘ +40∘ = 180∘ (Angles of ΔADE)
x = 180∘– 90∘
x = 90∘
Therefore, we can conclude that the required angles are 50∘, 40∘ and 90∘.
Q16. If one angle of a triangle is 60∘ and the other two angles are in the ratio 1 :2, find the angles
Solution.
We know that one of the angles of the given triangle is 60∘. (Given)
We also know that the other two angles of the triangle are in the ratio 1 : 2.
Let one of the other two angles be x.
Therefore, the second one will be 2x.
We know that the sum of all the three angles of a triangle is equal to 180∘.
60∘ +x + 2x = 180∘
3x =180∘– 60∘
3x = 120∘
x = 120∘/3
x = 40∘
2x = 2 x 40
2x = 80∘
Hence, we can conclude that the required angles are 40∘ and 80∘.
Q17. It one angle of a triangle is 100∘ and the other two angles are in the ratio 2 : 3. find the angles.
Solution.
We know that one of the angles of the given triangle is 100∘.
We also know that the other two angles are in the ratio 2 : 3.
Let one of the other two angles be 2x.
Therefore, the second angle will be 3x.
We know that the sum of all three angles of a triangle is 180∘.
100∘ + 2x + 3x = 180∘
5x = 180∘– 100∘
5x = 80∘
x = 80∘/5
2x = 2 x 16
2x = 32∘
3x = 3 x 16
3x = 48∘
Thus, the required angles are 32∘ and 48∘.
Q18. In ΔABC, if 3∠A = 4∠B = 6∠C, calculate the angles.
Solution.
We know that for the given triangle, 3∠A=6∠C
∠A = 2∠C—(i)
We also know that for the same triangle, 4∠B = 6∠C
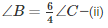
We know that the sum of all three angles of a triangle is 180∘.
Therefore, we can say that:
∠A+∠B+∠C=180∘ (Angles of ΔABC)—(iii)
On putting the values of ∠Aand∠B in equation (iii), we get :
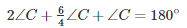
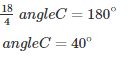
From equation (i), we have:
angleA = 2∠C = 2×40
angleA = 80∘
From equation (ii), we have:
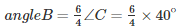
angleB = 60∘
angleA = 80∘, angleB = 60∘, angleC = 40∘
Therefore, the three angles of the given triangle are 80∘, 60∘, and 40∘.
Q19. Is it possible to have a triangle, in which
(i) Two of the angles are right?
(ii) Two of the angles are obtuse?
(iii) Two of the angles are acute?
(iv) Each angle is less than 60∘?
(v) Each angle is greater than 60∘?
(vi) Each angle is equal to 60∘
Give reasons in support of your answer in each case.
Solution.
(i) No, because if there are two right angles in a triangle, then the third angle of the triangle must be zero, which is not possible.
(ii) No, because as we know that the sum of all three angles of a triangle is always 180∘. If there are two obtuse angles, then their sum will be more than 180∘, which is not possible in case of a triangle.
(iii) Yes, in right triangles and acute triangles, it is possible to have two acute angles.
(iv) No, because if each angle is less than 60∘, then the sum of all three angles will be less than 180∘, which is not possible in case of a triangle.
Proof:
Let the three angles of the triangle be ∠A, ∠B and ∠C.
As per the given information,
∠A < 60∘ … (i)
∠B< 60∘ …(ii)
∠C< 60∘ … (iii)
On adding (i), (ii) and (iii), we get :
∠A + ∠B + ∠C < 60∘+ 60∘+ 60∘
∠A + ∠B + ∠C < 180∘
We can see that the sum of all three angles is less than 180∘, which is not possible for a triangle.
Hence, we can say that it is not possible for each angle of a triangle to be less than 60∘.
(v) No, because if each angle is greater than 60∘, then the sum of all three angles will be greater than 180∘, which is not possible.
Proof:
Let the three angles of the triangle be ∠A, ∠B and ∠C. As per the given information,
∠A > 60∘ … (i)
∠B>60∘ …(ii)
∠C> 60∘ … (iii)
On adding (i), (ii) and (iii), we get:
∠A + ∠B + ∠C > 60∘+ 60∘+ 60∘
∠A + ∠B + ∠C > 180∘
We can see that the sum of all three angles of the given triangle are greater than 180∘, which is not possible for a triangle.
Hence, we can say that it is not possible for each angle of a triangle to be greater than 60∘.
(vi) Yes, if each angle of the triangle is equal to 60∘ , then the sum of all three angles will be 180∘ , which is possible in case of a triangle.
Proof:
Let the three angles of the triangle be ∠A, ∠B and ∠C. As per the given information,
∠A = 60∘ … (i)
∠B = 60∘ …(ii)
∠C = 60∘ … (iii)
On adding (i), (ii) and (iii), we get:
∠A + ∠B + ∠C = 60∘+ 60∘+ 60∘
∠A + ∠B + ∠C = 180∘
We can see that the sum of all three angles of the given triangle is equal to 180∘, which is possible in case of a triangle. Hence, we can say that it is possible for each angle of a triangle to be equal to 60∘.
Q20. In ΔABC, ∠A = 100∘, AD bisects ∠A and AD perpendicular BC. Find ∠B
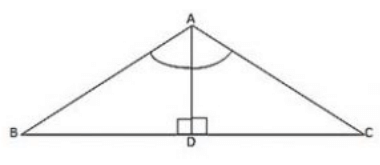
Solution.
Consider ΔABD
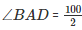 (AD bisects ∠A)
(AD bisects ∠A)
∠BAD = 50∘
∠ADB = 90∘ (AD perpendicular to BC)
We know that the sum of all three angles of a triangle is 180∘.
Thus,
∠ABD+∠BAD+∠ADB = 180∘ (Sum of angles of ΔABD)
Or,
∠ABD + 50∘ + 90∘ = 180∘
∠ABD = 180∘– 140∘
∠ABD = 40∘
Q21. In ΔABC, ∠A = 50∘, ∠B=100∘ and bisector of ∠C meets AB in D. Find the angles of the triangles ADC and BDC
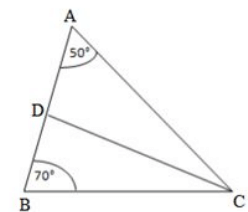
Solution.
We know that the sum of all three angles of a triangle is equal to 180∘.
Therefore, for the given ΔABC, we can say that :
∠A + ∠B + ∠C = 180∘ (Sum of angles of ΔABC)
50∘ + 70∘ + ∠C = 180∘
∠C = 180∘ –120∘
∠C = 60∘
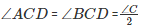 (CD bisects ∠C and meets AB in D.)
(CD bisects ∠C and meets AB in D.)
Using the same logic for the given ΔACD, we can say that :
∠DAC + ∠ACD + ∠ADC = 180∘
50∘ +30∘ +∠ADC = 180∘
∠ADC = 180∘ – 80∘
∠ADC = 100∘
If we use the same logic for the given ΔBCD, we can say that
∠DBC +∠BCD +∠BDC = 180∘
70∘ + 30∘ + ∠BDC = 180∘
∠BDC = 180∘ – 100∘
∠BDC = 80∘
Thus,
For ΔADC: ∠A = 50∘, ∠D = 100∘ ∠C = 30∘
ΔBDC: ∠B = 70∘, ∠D = 80∘ ∠C = 30∘
Q22. In ΔABC, ∠A=60∘, ∠B=80∘, and the bisectors of ∠B and ∠C, meet at O. Find
(i) ∠C
(ii) ∠BOC
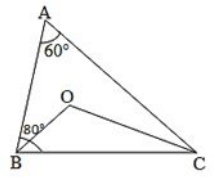
Solution.
We know that the sum of all three angles of a triangle is 180∘.
Hence, for ΔABC, we can say that :
∠A + ∠B + ∠C = 180∘ (Sum of angles of ΔABC)
60∘+ 80∘ + ∠C = 180∘.
∠C = 180∘ – 140∘
∠C = 140∘.
For ΔOBC,
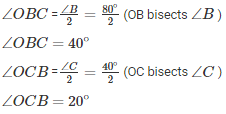
If we apply the above logic to this triangle, we can say that :
∠OCB + ∠OBC + ∠BOC = 180∘ (Sum of angles of ΔOBC)
20∘+ 40∘ +∠BOC = 180∘
∠BOC = 180∘ – 60∘
∠BOC = 120∘
Q23. The bisectors of the acute angles of a right triangle meet at O. Find the angle at O between the two bisectors.

Solution.
We know that the sum of all three angles of a triangle is 180∘.
Hence, for ΔABC , we can say that :
∠A + ∠B + ∠C = 180∘
∠A + 90∘ + ∠C = 180∘
∠A + ∠C = 180∘ – 90∘
∠A + ∠C = 90∘
For ΔOAC :
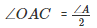 (OA bisects LA)
(OA bisects LA)
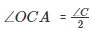 (OC bisects LC)
(OC bisects LC)
On applying the above logic to ΔOAC, we get :
∠AOC+ ∠OAC+∠OCA = 180∘ (Sum of angles of ΔAOC)
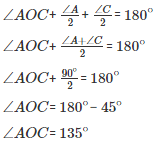
Q24. In ΔABC, ∠A = 50∘ and BC is produced to a point D. The bisectors of ∠ABC and ∠ACD meet at E. Find ∠E .
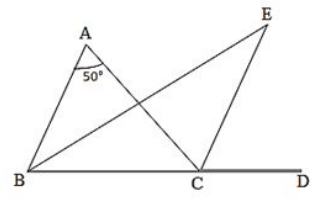
Solution.
In the given triangle,
∠ACD = ∠A + ∠B. (Exterior angle is equal to the sum of two opposite interior angles.)
We know that the sum of all three angles of a triangle is 180∘.
Therefore, for the given triangle, we can say that :
∠ABC+ ∠BCA + ∠CAB = 180∘ (Sum of all angles of ΔABC)
∠A + ∠B + ∠BCA = 180∘
∠BCA = 180°- (∠A + ∠B)
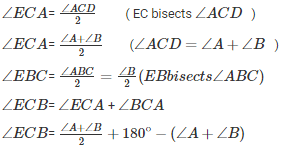
If we use the same logic for ΔEBC , we can say that :
∠EBC+ ∠ECB + ∠BEC = 180∘ (Sum of all angles of ΔEBC)
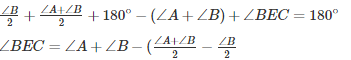
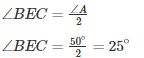
Q25. In ΔABC, ∠B=60∘, ∠C=40∘, AL perpendicular BC and AD bisects ∠A such that L and D lie on side BC. Find ∠LAD
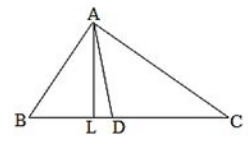
Solution.
We know that the sum of all angles of a triangle is 180∘
Therefore, for ΔABC, we can say that :
∠A + ∠B + ∠C = 180∘
Or,
∠A + 60∘ + 40∘ = 180∘
∠A = 80∘
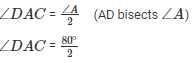
If we use the above logic on ΔADC, we can say that :
∠ADC + ∠DCA + ∠DAC = 180∘ (Sum of all the angles of ΔADC)
∠ADC + 40∘ + 40∘ = 180∘
∠ADC = 180∘ + 80∘
∠ADC = ∠ALD + ∠LAD(Exterior angle is equal to the sum of two Interior opposite angles.)
100∘ = 90∘+ ∠LAD (AL perpendicular to BC)
∠LAD = 90∘
Q26. Line segments AB and CD intersect at O such that AC perpendicular DB. It ∠CAB = 35∘ and ∠CDB = 55∘ . Find ∠BOD.
Solution.
We know that AC parallel to BD and AB cuts AC and BD at A and B, respectively.
∠CAB = ∠DBA (Alternate interior angles)
∠DBA = 35∘
We also know that the sum of all three angles of a triangle is 180∘.
Hence, for ΔOBD, we can say that :
∠DBO + ∠ODB+ ∠BOD = 180∘
35∘ + 55∘ + ∠BOD = 180∘ (∠DBO =∠DBA and ∠ODB =∠CDB)
∠BOD =180∘ − 90∘
∠BOD = 90∘
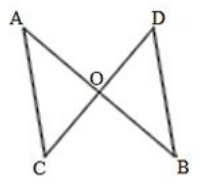
Q27. In Fig. 22, ΔABC is right angled at A, Q and R are points on line BC and P is a point such that QP perpendicular to AC and RP perpendicular to AB. Find ∠P
Solution.
In the given triangle, AC parallel to QP and BR cuts AC and QP at C and Q, respectively.
∠QCA = ∠CQP (Alternate interior angles)
Because RP parallel to AB and BR cuts AB and RP at B and R, respectively,
∠ABC = ∠PRQ (alternate interior angles).
We know that the sum of all three angles of a triangle is 180∘.
Hence, for ΔABC, we can say that :
∠ABC + ∠ACB + ∠BAC = 180∘
∠ABC + ∠ACB + 90∘ = 180∘ (Right angled at A)
∠ABC + ∠ACB = 90∘
Using the same logic for ΔPQR, we can say that :
∠PQR + ∠PRQ + ∠QPR = 180∘
∠ABC + ∠ACB + ∠QPR =180∘ (∠ABC = ∠PRQ and ∠QCA =∠CQP)
Or,
90∘ + ∠QPR = 180∘ (∠ABC+ ∠ACB = 90∘)
∠QPR = 90∘
FAQs on Ex-15.2, (Part - 2), Properties Of Triangles, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are the properties of triangles? |  |
| 2. How can I find the missing angle in a triangle? |  |
| 3. What is the Pythagorean theorem and how does it relate to triangles? |  |
| 4. How can I determine if a triangle is equilateral, isosceles, or scalene? |  |
| 5. Can a triangle have more than one right angle? |  |

|
Explore Courses for Class 7 exam
|

|

















