Ex-15.3, (Part - 1), Properties Of Triangles, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
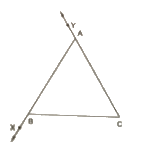
1. ∠CBX is an exterior angle of ΔABC at B. Name
(i) the interior adjacent angle
(ii) the interior opposite angles to exterior ∠CBX
Also, name the interior opposite angles to an exterior angle at A.
Solution.
(i) ∠ABC
(ii) ∠BAC and ∠ACB
Also the interior angles opposite to exterior are ∠ABC and ∠ACB
2. In the fig, two of the angles are indicated. What are the measures of ∠ACX and ∠ACB?

Solution.
In ΔABC, ∠A = 50° and ∠B = 55°
Because of the angle sum property of the triangle, we can say that
∠A+∠B+∠C = 180°
50° +55° +∠C = 180°
Or
∠C=75°
∠ACB = 75°
∠ACX = 180°−∠ACB = 180°−75° = 105°
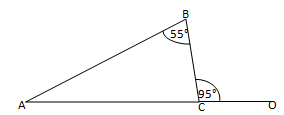
3. In a triangle, an exterior angle at a vertex is 95° and its one of the interior opposite angles is 55°. Find all the angles of the triangle.
Solution.
We know that the sum of interior opposite angles is equal to the exterior angle.
Hence, for the given triangle, we can say that :
∠ABC+ ∠BAC = ∠BCO
55° + ∠BAC = 95°
Or,
∠BAC = 95°– 95°
= ∠BAC = 40°
We also know that the sum of all angles of a triangle is 180°.
Hence, for the given ΔABC, we can say that :
∠ABC + ∠BAC + ∠BCA = 180°
55° + 40° + ∠BCA = 180°
Or,
∠BCA =180° –95°
= ∠BCA = 85°
4. One of the exterior angles of a triangle is 80°, and the interior opposite angles are equal to each other. What is the measure of each of these two angles?
Solution.
Let us assume that A and B are the two interior opposite angles.
We know that ∠A is equal to ∠B.
We also know that the sum of interior opposite angles is equal to the exterior angle.
Hence, we can say that :
∠A + ∠B = 80°
Or,
∠A +∠A = 80° (∠A= ∠B)
2∠A = 80°
∠A = 40°2 =40°
∠A= ∠B = 40°
Thus, each of the required angles is of 40°.
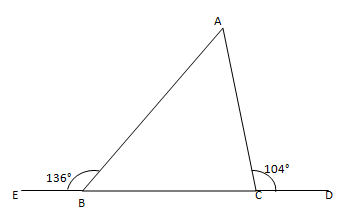
5. The exterior angles, obtained on producing the base of a triangle both ways are 104° and 136°. Find all the angles of the triangle.
Solution.
In the given figure, ∠ABE and ∠ABC form a linear pair.
∠ABE + ∠ABC =180°
∠ABC = 180°– 136°
∠ABC = 44°
We can also see that ∠ACD and ∠ACB form a linear pair.
∠ACD + ∠ACB = 180°
∠AUB= 180°– 104°
∠ACB = 76°
We know that the sum of interior opposite angles is equal to the exterior angle.
Therefore, we can say that :
∠BAC + ∠ABC =104°
∠BAC = 104°– 44° = 60°
Thus,
∠ACE = 76°
and
∠BAC = 60°
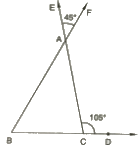
6. In Fig, the sides BC, CA and BA of a ΔABC have been produced to D, E and F respectively. If ∠ACD=105° and ∠EAF=45° ; find all the angles of the ΔABC
Solution.
In a ΔABC, ∠BAC and ∠EAF are vertically opposite angles.
Hence, we can say that :
∠BAC= ∠EAF = 45°
Considering the exterior angle property, we can say that :
∠BAC + ∠ABC = ∠ACD = 105°
∠ABC = 105°– 45° = 60°
Because of the angle sum property of the triangle, we can say that :
∠ABC+ ∠ACS +∠BAC = 180°
∠ACB = 75°
Therefore, the angles are 45°, 65° and 75°.
7. In Fig, AC perpendicular to CE and C ∠A:∠B:∠C=3:2:1. Find the value of ∠ECD.
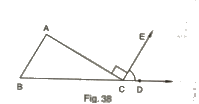
Solution.
In the given triangle, the angles are in the ratio 3 : 2 : 1.
Let the angles of the triangle be 3x, 2x and x.
Because of the angle sum property of the triangle, we can say that :
3x+2x+x = 180°
6x = 180°
Or,
x = 30° … (i)
Also, ∠ACB + ∠ACE + ∠ECD = 180°
x+ 90° + ∠ECD = 180° (∠ACE = 90° )
∠ECD= 60° [From (i)]
8 A student when asked to measure two exterior angles of ΔABC observed that the exterior angles at A and B are of 103° and 74° respectively. Is this possible? Why or why not?
Here,
Solution.
Internal angle at A+ External angle at A = 180°
Internal angle at A + 103° =180°
Internal angle at A = 77°
Internal angle at B + External angle at B = 180°
Internal angle at B + 74° = 180°
Internal angle at B = 106°
Sum of internal angles at A and B = 77° + 106° =183°
It means that the sum of internal angles at A and B is greater than 180°, which cannot be possible.
9. In Fig, AD and CF are respectively perpendiculars to sides BC and AB of ΔABC. If ∠FCD=50°, find ∠BAD
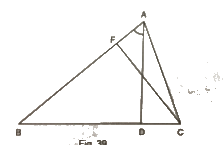
Solution.
We know that the sum of all angles of a triangle is 180°
Therefore, for the given ΔFCB, we can say that :
∠FCB+ ∠CBF+ ∠BFC= 180°
50° + ∠CBF + 90°= 180°
Or,
∠CBF = 180° –50°– 90° = 40° … (i)
Using the above rule for ΔABD, we can say that :
∠ABD + ∠BDA + ∠BAD = 180°
∠BAD = 180° –90°– 40° = 50° [from (i)]
10. In Fig, measures of some angles are indicated. Find the value of x.
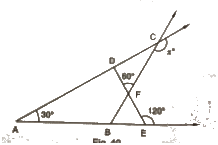
Solution.
Here,
∠AED + 120° = 180° (Linear pair)
∠AED = 180°– 120° = 60°
We know that the sum of all angles of a triangle is 180°.
Therefore, for ΔADE, we can say that :
∠ADE + ∠AED + ∠DAE = 180°
60°+ ∠ADE + 30° =180°
Or,
∠ADE =180°– 60°– 30° = 90°
From the given figure, we can also say that :
∠FDC + 90° = 180° (Linear pair)
∠FDC = 180°– 90° = 90°
Using the above rule for ΔCDF, we can say that :
∠CDF + ∠DCF + ∠DFC = 180°
90° + ∠DCF + 60° =180°
∠DCF = 180°−60°−90°= 30°
Also,
∠DCF + x = 180° (Linear pair)
30° + x = 180°
Or,
x = 180°– 30° = 150°
FAQs on Ex-15.3, (Part - 1), Properties Of Triangles, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are the properties of triangles? |  |
| 2. How do you find the sum of the angles in a triangle? |  |
| 3. What is the Triangle Inequality Theorem? |  |
| 4. How can you determine if three given side lengths can form a triangle? |  |
| 5. What is the relationship between the exterior angle of a triangle and its opposite interior angles? |  |





















