Ex-15.4, Properties Of Triangles, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Q1. In each of the following, there are three positive numbers. State if these numbers could possibly be the lengths of the sides of a triangle:
(i) 5, 7, 9
(ii) 2, 10.15
(iii) 3, 4, 5
(iv) 2, 5, 7
(v) 5, 8, 20
Solution.
(i) Yes, these numbers can be the lengths of the sides of a triangle because the sum of any two sides of a triangle is always greater than the third side. Here, 5+7>9, 5+9>7, 9+7>5
(ii) No, these numbers cannot be the lengths of the sides of a triangle because the sum of any two sides of a triangle is always greater than the third side, which is not true in this case.
(iii) Yes, these numbers can be the lengths of the sides of a triangle because the sum of any two sides of triangle is always greater than the third side. Here, 3+4 >5, 3+5> 4, 4+5> 3
(iv) No, these numbers cannot be the lengths of the sides of a triangle because the sum of any two sides of a triangle is always greater than the third side, which is not true in this case. Here, 2 + 5 = 7
(v) No, these numbers cannot be the lengths of the sides of a triangle because the sum of any two sides of a triangle is always greater than the third side, which is not true in this case. Here, 5 + 8 <20
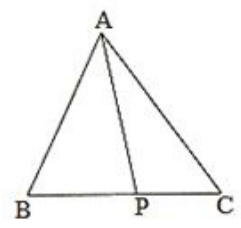
Q2. In Fig, P is the point on the side BC. Complete each of the following statements using symbol ‘ =’,’ > ‘or ‘ < ‘so as to make it true:
(i) AP… AB+ BP
(ii) AP… AC + PC
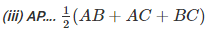
Solution.
(i) In triangle APB, AP < AB + BP because the sum of any two sides of a triangle is greater than the third side.
(ii) In triangle APC, AP < AC + PC because the sum of any two sides of a triangle is greater than the third side.
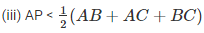 In triangles ABP and ACP, we can see that:
In triangles ABP and ACP, we can see that:
AP < AB + BP…(i) (Because the sum of any two sides of a triangle is greater than the third side)
AP < AC + PC…(ii) (Because the sum of any two sides of a triangle is greater than the third side)
On adding (i) and (ii), we have:
AP + AP < AB + BP + AC + PC
2AP < AB + AC + BC (BC = BP + PC)
AP < (AB-FAC+BC)
Q3. P is a point in the interior of ΔABC as shown in Fig. State which of the following statements are true (T) or false (F):
(i) AP+ PB< AB
(ii) AP+ PC> AC
(iii) BP+ PC = BC
Solution.
(i) False
We know that the sum of any two sides of a triangle is greater than the third side: it is not true for the given triangle.
(ii) True
We know that the sum of any two sides of a triangle is greater than the third side: it is true for the given triangle.
(iii) False
We know that the sum of any two sides of a triangle is greater than the third side: it is not true for the given triangle.
Q4. O is a point in the exterior of ΔABC. What symbol ‘>’,’<’ or ‘=’ will you see to complete the statement OA+OB….AB? Write two other similar statements and show that
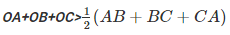
Solution.
Because the sum of any two sides of a triangle is always greater than the third side, in triangle OAB, we have:
OA+OB> AB —(i)
OB+OC>BC —-(ii)
OA+OC > CA —–(iii)
On adding equations (i), (ii) and (iii) we get :
OA+OB+OB+OC+OA+OC> AB+BC+CA
2(OA+OB+OC) > AB+BC +CA
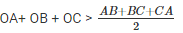
Q5. In △ABC, ∠B=30∘, ∠C=50∘. Name the smallest and the largest sides of the triangle.
Solution.
Because the smallest side is always opposite to the smallest angle, which in this case is 30∘, it is AC. Also, because the largest side is always opposite to the largest angle, which in this case is 100∘,, it is BC.
FAQs on Ex-15.4, Properties Of Triangles, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are the properties of triangles? |  |
| 2. How do you find the measure of an exterior angle of a triangle? |  |
| 3. What is the Triangle Inequality Theorem? |  |
| 4. How do you prove that the interior angles of a triangle add up to 180 degrees? |  |
| 5. How can you determine if three given side lengths form a triangle? |  |

|
Explore Courses for Class 7 exam
|

|

















