Ex-16.1 , Congruence, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
Explain the concept of congruence of figures with the help of certain examples.
Answer 1:
Congruent objects or figures are exact copies of each other or we can say mirror images of each other. The relation of two objects being congruent is called congruence.
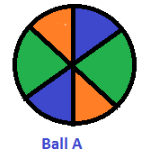
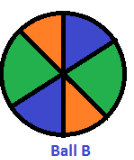
Consider Ball A and Ball B. These two balls are congruent.
Now consider the two stars below. Star A and Star B are exactly the same in size, colour and shape. These are congruent stars.


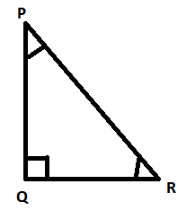
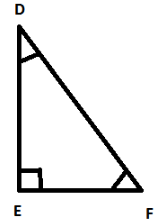
Let us look at the triangles below, Here we have triangle PQR and triangle DEF.
These two triangles have corresponding angles equal and corresponding sides equal. Thus these triangles are congruent to each other.
Question 2:
Fill in the blanks:
(i) Two line segments are congruent if .......
(ii) Two angles are congruent if ......
(iii) Two squres are congruent if .......
(iv) Two rectangles are congruent if .......
(v) Two circles are congruent if .......
Answer 2:
1) They have the same length, since they can superpose on each other.
2) Their measures are the same. On superposition, we can see that the angles are equal.
3) Their sides are equal. All the sides of a square are equal and if two squares have equal sides, then all their sides are of the same length. Also angles of a square are 90o which is also the same for both the squares.
4) Their lengths are equal and their breadths are also equal. The opposite sides of a rectangle are equal. So if two rectangles have lengths of the same size and breadths of the same size, then they are congruent to each other.
5) Their radii are of the same length. Then the circles will have the same diameter and thus will be congruent to each other.
Question 3:
In Fig., ∠POQ ≅ ∠ROS, can we say that ∠POR ≅ ∠QOS
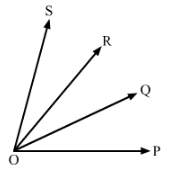
Answer 3:
We have,
∠POQ ≅∠ROS (1)
Also, ∠ROQ ≅∠ROQ (same angle)
Therefore, adding ∠ROQ to both sides of (1), we get:
∠POQ +∠ROQ ≅∠ROQ +∠ROS
Therefore, ∠POR ≅ ∠QOS
Hence proved.
Question 4:
In Fig., a = b = c, name the angle which is congruent to ∠AOC.
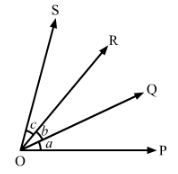
Answer 4:
We have,
∠AOB =∠BOC = ∠COD
Therefore, ∠AOB =∠COD
Also, ∠AOB +∠BOC=∠BOC +∠COD
∠AOC=∠BOD
Hence, ∠AOC≅∠BOD
∠BODis congruent to ∠AOC
Question 5:
Is it correct to say that any two right angles are congruent? Give reasons to justify your answer.
Answer 5:
Two right angles are congruent to each other because they both measure 90 degrees.
We know that two angles are congruent if they have the same measure.
Question 6:
In Fig. 8, ∠AOC ≅ ∠PYR and ∠BOC ≅ ∠QYR. Name the angle which is congruent to ∠AOB.
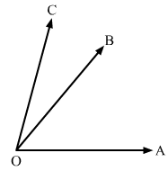
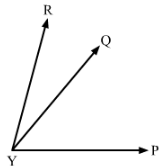
Answer 6:
∠AOC ≅∠PYR..........(i)Also, ∠BOC ≅∠QYR
Now, ∠AOC = ∠AOB +∠BOC and ∠PYR =∠PYQ +∠QYR
By putting the value of∠AOC and ∠PYR in equation(i), we get:
∠AOB +∠BOC ≅∠PYQ +∠QYR
∠AOB ≅∠PYQ (∠BOC ≅∠QYR)
Hence ∠AOB ≅∠PYQ
Question 7:
Which of the following statements are true and which are false;
(i) All squares are congruent.
(ii) If two squares have equal areas, they are congruent.
(iii) If two rectangles have equal area, they are congruent.
(iv) If two triangles are equal in area, they are congruent.
Answer 7:
i) False. All the sides of a square are of equal length. However, different squares can have sides of different lengths. Hence all squares are not congruent.
ii) True
Area of a square = side ××side
Therefore, two squares that have the same area will have sides of the same lengths. Hence they will be congruent.
iii) False
Area of a rectangle = length ×× breadth
Two rectangles can have the same area. However, the lengths of their sides can vary and hence they are not congruent.
Example: Suppose rectangle 1 has sides 8 m and 8 m and area 64 metre square.
Rectangle 2 has sides 16 m and 4 m and area 64 metre square.
Then rectangle 1 and 2 are not congruent.
iv) False
Area of a triangle = 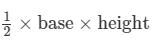
Two triangles can have the same area but the lengths of their sides can vary and hence they cannot be congruent.
FAQs on Ex-16.1 , Congruence, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What is the concept of congruence in math? |  |
| 2. How can we determine if two triangles are congruent? |  |
| 3. What is the importance of congruence in real-life applications? |  |
| 4. Can congruence be used to prove the equality of two lengths or angles? |  |
| 5. What are some common misconceptions about congruence in math? |  |

|
Explore Courses for Class 7 exam
|

|


















