Ex-16.3, Congruence, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
By applying SAS congruence condition, state which of the following pairs (Fig. 28) of triangles are congruent. State the result in symbolic form
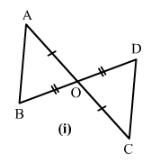
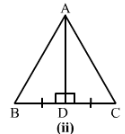
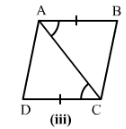
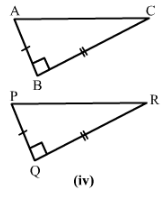
Answer 1:
1) We have OA = OC and OB = OD and∠AOB =∠COD which are vertically opposite angles.
Therefore by SAS condition, △AOC ≅ △BOD.
2) We have BD = DC
∠ADB =∠ADC = 90°
and AD = AD
Therefore by SAS condition, △ADB ≅ △ADC.
3) We have AB = DC
∠∠ABD = ∠CDB and BD = DB
Therefore by SAS condition, △ABD ≅ △CBD.
4) We have BC = QR
∠ABC =∠PQR = 90°
and AB = PQ
Therefore by SAS condition, △ABC ≅ △PQR.
Question 2:
State the condition by which the following pairs of triangles are congruent.
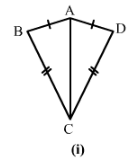
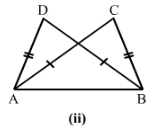
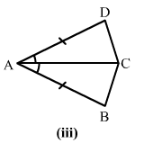
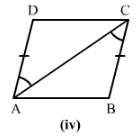
Answer 2:
1) AB = AD
BC = CD
and AC = CA
Therefore by SSS condition, △ABC≅△ADC.
2) AC = BD
AD = BC and AB = BA
Therefore by SSS condition, △ABD≅△BAC.
3) AB = AD
∠BAC=∠DAC∠BAC=∠DAC
and AC = AC
Therefore by SAS condition, △BAC≅△DAC.
4) AD = BC
∠ DAC = ∠BCA
and AC = CA
Therefore by SAS condition, △ABC≅△ADC.
Question 3:
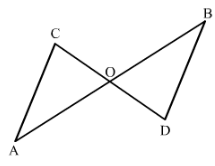
In Fig. 30, line segments AB and CD bisect each other at O. Which of the following statements is true?
(i) ∆ AOC ≅ ∆ DOB
(ii) ∆ AOC ≅ ∆ BOD
(iii) ∆ AOC ≅ ∆ ODB.
State the three pairs of matching parts, yut have used to arive at the answer.
Answer 3:
We have AO = OB.
And CO = OD
Also ∠AOC = ∠BOD
Therefore by SAS condition, △AOC ≅ △BOD.
Therefore, statement (ii) is true.
Question 4:
Line-segments AB and CD bisect each other at O. AC and BD are joined forming triangles AOC and BOD. State the three equality relations between the parts of the two triangles, that are given or otherwise known. Are the two triangles congruent? State in symbolic form. Which congruence condition do you use?
Answer 4:
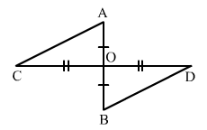
We have AO = OB and CO = OD since AB and CD bisect each other at O.
Also ∠AOC = ∠BOD since they are opposite angles on the same vertex.
Therefore by SAS congruence condition,
△AOC≅△BOD
Question 5:
∆ ABC is isosceles with AB = AC. Line segment AD bisects ∠A and meets the base BC in D.
(i) Is ∆ ADB ≅ ∆ ADC?
(ii) State the three pairs of matching parts used to answer (i).
(iii) Is it true to say that BD = DC?
Answer 5:
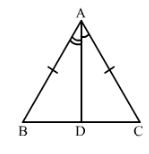
(i) We have AB = AC (given)
∠BAD =∠CAD∠BAD =∠CAD (AD bisects ∠BAC)
and AD = AD (common)
Therefore by SAS condition of congruence, △ABD≅△ACD
(ii) We have used AB, AC; ∠BAD =∠CAD; AD, DA.
(iii) Now△ABD≅△ACD therefore by c.p.c.t BD = DC.
Question 6:
In Fig. 31, AB = AD and ∠BAC = ∠DAC.
(i) State in symbolic form the congruence of two triangles ABC and ADC that is true.
(ii) Complete each of the following, so as to make it true:
(a) ∠ABC = ........
(b) ∠ACD = ........
(c) Line segment AC bisects ..... and .....
Answer 6:
i) AB = AD (given)
∠BAC =∠DAC (given)
AC = CA (common)
Therefore by SAS conditionof congruency, △ABC ≅△ADC
ii) ∠ABC =∠ADC (c.p.c.t)
∠ACD =∠ACB (c.p.c.t)
Question 7:
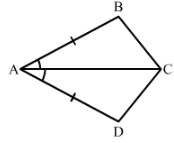
In Fig. 32, AB || DC and AB = DC.
(i) Is ∆ ACD ≅ ∆ CAB?
(ii) State the three pairs of matching parts used to answer (i).
(iii) Which angle is equal to ∠CAD?
(iv) Does it follow from (iii) that AD || BC?
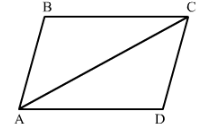
Answer 7:
(i) Yes △ACD≅△CAB by SAS condition of congruency.
(ii) We have used AB = DC, AC = CA and ∠DCA=∠BAC.
(iii) ∠CAD =∠ACB since the two triangles are congruent.
(iv) Yes, this follows from AD∥∥BC as alternate angles are equal.If alternate angles are equal the lines are parallel.
FAQs on Ex-16.3, Congruence, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are the basic concepts of congruence in mathematics? |  |
| 2. How can congruence be used to solve geometric problems? |  |
| 3. What are the different methods to prove congruence between two triangles? |  |
| 4. Can congruence only be applied to triangles or can it be applied to other shapes as well? |  |
| 5. How does understanding congruence help in real-life applications? |  |
















