Ex-16.4, Congruence, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
Which of the following pairs of triangles are congruent by ASA condition?
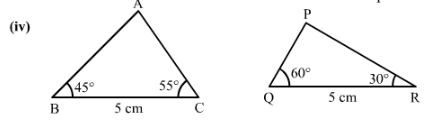
Answer 1:
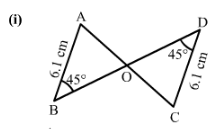
1) We have
Since ∠ABO = ∠CDO = 45° and both are alternate angles,
AB∥DC
∠BAO = ∠DCO (alternate angle , AB∥CD and AC is a transversal line)
∠ABO = ∠CDO = 45° (given in the figure)
Also, AB = DC (Given in the figure)
Therefore, by ASA △AOB ≅△DOC
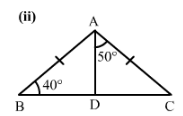
2)
In △ABC ,
Now AB = AC (Given)
∠ABD = ∠ACD = 40° (Angles opposite to equal sides)
∠ABD +∠ACD+∠BAC=180° (Angle sum property)
40°+40°+∠BAC=180°
∠BAC=180°-80°=100°
∠BAD +∠DAC=∠BAC
∠BAD=∠BAC-∠DAC=100°-50°=50°
∠BAD =∠CAD = 50°
Therefore, by ASA, △ABD ≅△ADC
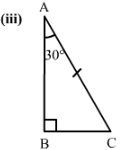
3)
InΔABC,
∠A+∠B+∠C=180°(Angle sum property)
∠C=180°-∠A-∠B
∠C=180°-30°-90°=60°
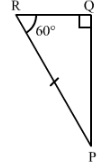
InΔPQR,
∠P+∠Q+∠R=180°(Angle sum property)
∠P=180°-∠Q-∠R
∠P=180°-60°-90°=30°
∠BAC = ∠QPR = 30°
∠BCA=∠PRQ = 60°
and AC = PR (Given)
Therefore, by ASA, △ABC ≅△PQR
4)
We have only BC =QR but none of the angles of △ABC AND △PQR are equal.
Therefore, △ABC≆ △PRQ
Question 2:
In Fig. 37, AD bisects ∠A and AD ⊥ BC.
(i) Is ∆ ADB ≅ ∆ ADC?
(ii) State the three pairs of matching parts you have used in (i).
(iii) Is it true to say that BD = DC?
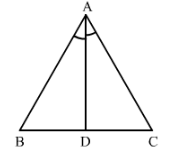
Answer 2:
(i) Yes, △ADB ≅△ADC, by ASA criterion of congruency
(ii) We have used ∠BAD =∠CAD
∠ADB=∠ADC = 90° since AD⊥BC
and AD = DA
(iii) Yes, BD= DC since, △ADB ≅△ADC
Question 3:
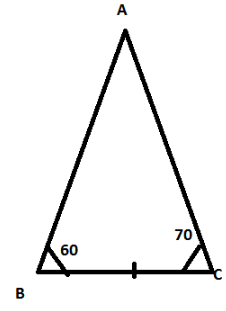
Draw any triangle ABC. Use ASA condition to construct another triangle congruent to it.
Answer 3:
We have drawn
△ABC with ∠ABC = 60°and ∠ACB = 70°
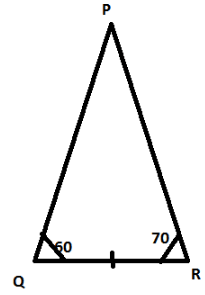
We now construct △PQR≅△ABC
△PQR has ∠PQR =60° and ∠PRQ = 70°
Also we construct △PQR such that BC =QR
Therefore by ASA the two triangles are congruent
Question 4:
In ∆ ABC, it is known that ∠B = ∠C. Imagine you have another copy of ∆ ABC
(i) Is ∆ ABC ≅ ∆ ACB?
(ii) State the three pairs of matching parts you have used to answer (i).
(iii) Is it true to say that AB = AC?
Answer 4:
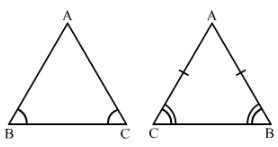
(i) Yes△ABC ≅△ACB
(ii) We have used ∠ABC=∠ACB and ∠ACB =∠ABC again
Also BC = CB
(iii) Yes, it is true to say that AB = AC since ∠ABC=∠ACB
Question 5:
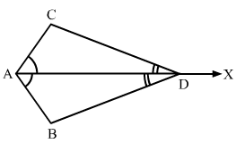
In Fig. 38, AX bisects ∠BAC as well as ∠BDC. State the three facts needed to ensure that ∆ ABD ≅ ∆ ACD.
Answer 5:
As per the given conditions,∠CAD=∠BAD and ∠CDA=∠BDA (because AX bisects ∠BAC ) AD=DA (common)
Therefore, by ASA, △ACD≅△ABD
Question 6:
In Fig. 39, AO = OB and ∠A = ∠B.
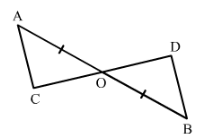
(i) Is ∆ AOC ≅ ∆ BOD?
(ii) State the matching pair you have used, which is not given in the question.
(iii) Is it true to say that ∠ACO = ∠BDO?
Answer 6:
We have
∠OAC =∠OBD, AO = OBAlso, ∠AOC = ∠BOD (Opposite angles on same vertex)
Therefore, by ASA △AOC ≅△BOD
FAQs on Ex-16.4, Congruence, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What is the concept of congruence in mathematics? |  |
| 2. How is congruence represented in mathematical notation? |  |
| 3. What are the different criteria to prove congruence of triangles? |  |
| 4. How can congruence be used to solve geometric problems? |  |
| 5. What are some real-life applications of congruence in mathematics? |  |
















