Ex-12.1, Triangles, Class 6, Maths RD Sharma Solutions | RD Sharma Solutions for Class 6 Mathematics PDF Download
1.Take three non- collinear points A, B and C on a page of your notebook. Join AB, BC and CA. what figure do you get? Name the triangle. Also, name
(i) the side opposite to ∠B ∠B
(ii) the angle opposite to side AB
(iii) the vertex opposite to site BC
(iv) the side opposite to vertex B
Solution: Let us consider three non- collinear points A, B and C join them. After joining these points, we get a ‘triangle’, as it consists of three sides. The name of the triangle we get is
ΔABC
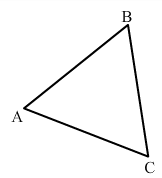
(i) The side opposite ∠B is AC
(ii) The angle opposite side AB is ∠C∠C
(iii) The vertex opposite side BC is A
(iv) The side opposite vertex B is AC
2.Take three collinear points A, B and C on a page of your note book. Join AB, BC and CA. Is the figure a triangle? If not why
Solution: Let us consider three collinear points A, B and C and join AB, BC and CA
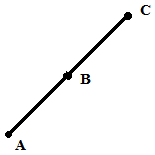
The figure we get is not a triangle because it is a straight line consisting of only one side. It is also not a closed figure, where as a triangle is defined as a closed figure consisting of three sides
3.Distinguish between a triangle and its triangular region.
Solution: A triangle is defined as a closed polygon consisting of three sides, where as a triangular region is the region that lies inside the triangle. In the adjoining figure, the shaded region shows the triangular region.

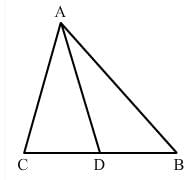
4.In fig 12.11, D is a point on side BC of a ΔABC. AD is joined. Name all the triangles that you can observe in the figure. How many are they?
Solution: The figure consists of triangles ΔADC, ΔADC and ΔABC. Therefore, three triangles are present in the figure.
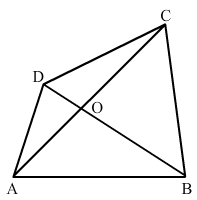
5.In fig 12.12, A, B, C and D are four points, and no three points are collinear. AC and BD interest at O. There are eight triangles that you can observe. Name all the triangles.
Solution: The following figure consists of triangles, namely
ΔODC, ΔODA, ΔOBC, ΔOAB, ΔADB, ΔACB, ΔDAC and ΔDBC. Hence, there are a total of eight triangles.
6.What is the difference between triangle and a triangular region?
Solution:
A triangle is defined as a closed polygon consisting of three sides, where as a triangular region is the region that lies inside the three sides of triangles.
In the adjoining figure, the shaded region shows the triangular region

7.Explain the following terms:
i. Triangle
ii. Parts or elements of a triangle
iii. Scalene triangle
iv. Isosceles triangle
v. Equilateral triangle
vi. Acute triangle
vii. Right triangle
viii. Obtuse triangle
ix. interior of a triangle
x. exterior of a triangle
Solution:
(i) Triangle – a triangle is a closed polygon that consists of three straight lines as its sides.
(ii) Parts or elements of a triangle – a triangle consists of three sides, three angles and three vertices.
(iii) Scalene triangle – a triangle, in which the length of all the sides are different.
(iv) Isosceles triangle – a triangle, in which the length of two sides are equal.
(v) Equilateral triangle – a triangle, in which the length of all the sides are equal.
(vi) Acute triangles – a triangle, in which all the angles measure less than 90∘.|
(vii) Right triangle – a triangle, which has an angle that measure 90∘.
(viii) Obtuse triangle – a triangle, in which one of the angles measure more than 90∘.
(ix) Interior of a triangle – the region lying inside the boundaries or side of a triangle.
(x) Exterior of a triangle – the region lying outside the boundaries or sides of a triangle.
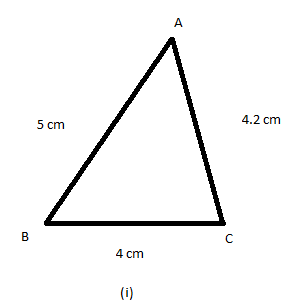
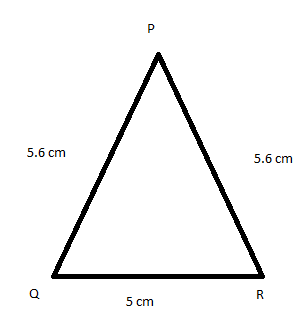
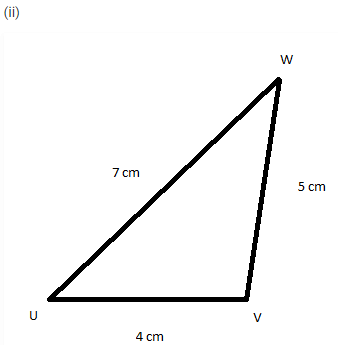
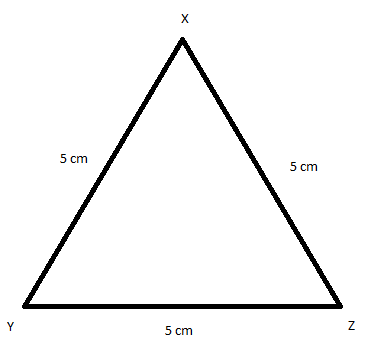
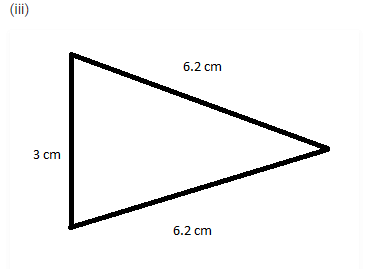
8. In fig 12.13, the length (in cm) of each side has been indicted along the side. State for each triangle whether it is a scalene, isosceles or equilateral:
(iv)
Solution:
(i) This is a scalene triangle, as all the sides have different length.
(ii) This is an isosceles triangle, as two sides are equal in length i.e. 5.6 cm.
(iii) This is an equilateral triangle, as all the sides are equal in length i.e. 5 cm.
(iv)This is a scalene triangle, as all the sides have different length.
(v) This is an isosceles triangle, as two sides are equal in length i.e. 6.2 cm.
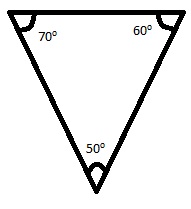
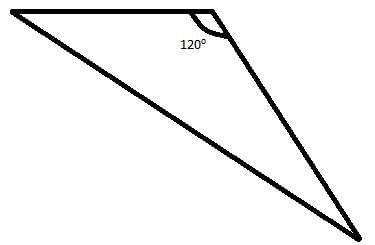
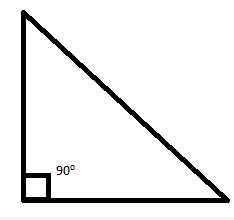
9. In fig 12.14, there are five triangles. The measures of some of their angles have been indicated. State for each triangle whether it is acute, right or obtuse.
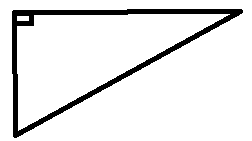
(i) (ii) (iii) (iv)
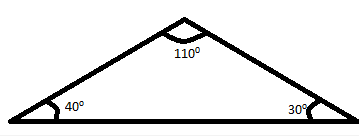
(v)
Solution:
(i) This is a right angle triangle, as it contains a 90∘.
(ii) This is an obtuse angle triangle, as one of the angle (90∘) measure more than 90∘ and less than 180∘.
(iii) This is an acute angle triangle, as all the angles are less than 90∘.
(iv) This is a right angles triangle, as it contains a 90∘ angle.
(v) This is an obtuse angled triangle, as one of the angle (110∘) measures more than 90∘ and less than 180∘.
10.Fill in the blanks with the correct world/ symbol to make it a true statement:
Solution.
(i) A triangle has three sides.
(ii) A triangle has three vertices.
(iii) A triangle has three angles.
(iv) A triangle has six parts.
(Angles and sides are part of a triangle. So, three angles and three sides make six parts.)
(v) A triangle whose no two sides are equal is known as Scalene triangle.
(A triangle whose lengths of all sides are different is called scalene triangle).
(vi) A triangle whose two sides are equal is known as Equilateral triangle.
(A triangle whose lengths of two sides are equal is called an equilateral triangle).
(vii) A triangle whose one angle is a right angle is known as Right angled triangle.
(A triangle whose one angle is 90∘ is called a right angle triangle).
(viii) A triangle whose all angles are less than 90∘ is known as an Acute triangle.
(A triangle whose all angle are less than 90∘ is known as Acute triangle).
(x) A triangle whose one side angle is more than 90∘ is known as an Obtuse triangle.
(A triangle whose one angle is more than 90∘ is called Obtuse triangle).
11.In each of the following, state if the statement is true or false:
Solution.
(i) True
(ii) False; a triangle consists of three vertices only.
(iii) False; three lines segments joined by three non- collinear points can only from a triangle.
(iv) False; it lies on the triangle.
(v) True
(vi) False; the vertices of a triangle are three non-collinear points.
(vii) True
(ix) False; it can also be an isosceles triangle.
(x) False; it can be an obtuse triangle.
FAQs on Ex-12.1, Triangles, Class 6, Maths RD Sharma Solutions - RD Sharma Solutions for Class 6 Mathematics
| 1. What are the different types of triangles? |  |
| 2. How do you determine if a triangle is equilateral? |  |
| 3. How can you find the area of a triangle? |  |
| 4. What is the Pythagorean theorem? |  |
| 5. How do you determine the similarity of two triangles? |  |

|
Explore Courses for Class 6 exam
|

|

















