Sawhorse formula into Newman projection formula- Stereochemistry PDF Download
We know that the left handed bottom end is towards the observer and right hand top end is away from the observer. We can convert this formula into Newman formula representing the molecule i.e. C2 which is towards observer by a dot (.) and the atom which is away from the observer that is C3 by a circle. The Newman projection formula is a planar projection of the sawhorse formula. In this molecule we view along the carbon-carbon bond. The carbon atom towards the observer is represented by a dot (.) and the
carbon atom away from the observer is represented by a circle. The above shown eclipsed form can be converted into staggered form by a rotation of 1800 of one carbon atom only.
Symmetry: Symmetry is all around us. In life, in art, in chemistry. It is defined in terms of elements and operations. Symmetry is likeness of shape or arrangement about a center.

Motif: The fundamental part of a symmetric design that, when repeated, creates the whole pattern
Operation:
Some act that reproduces the motif to create the same pattern. An operation can be rotation, reflection, inversion.
How do we know ? We rotate or reflect the object in our mind.
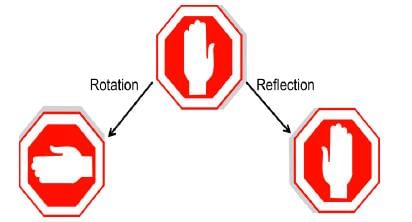
Element: An operation located at a particular point in space
Symmetry Elements
1. Identity
2. Proper axis of rotation
3. Mirror planes
4. Center of symmetry
5. Improper axis of rotation
Identity (E)
All molecules have Identity. This operation leaves the entire molecule unchanged. A highly asymmetric molecule such as a tetrahedral carbon with 4 different groups attached has only identity, and no other symmetry elements.
Rotation (Cn)
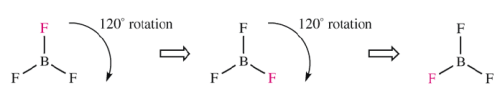
a. (C2) Two-fold rotation = 360o/2 rotation to reproduce a motif in a symmetrical pattern
b. (C3) Three-fold rotation = 360o/3 rotation to reproduce a motif in a symmetrical pattern
Similarly,
n = 4 gives 90o rotation (C4)
n = 6 gives 60o rotation (C6)
Principal axis of rotation (Cn) is one with the higest value of ‘n’.
Example:
Ammonia has a C3 axis. Note that there are two operations associated with the C3 axis. Rotation by 120o in clockwise or counter clockwise direction provide two different orientations of the molecule.
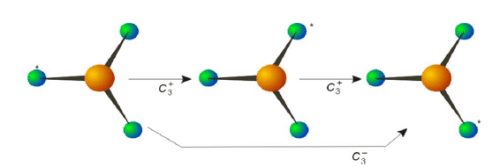
Rotations for a Trigonal Planar Molecule

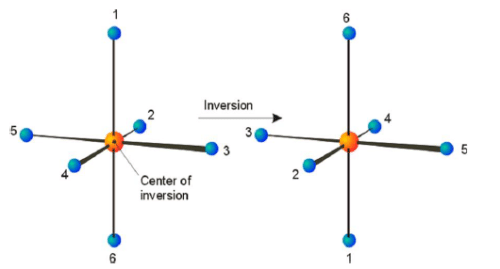
Center of symmetry (Ci)
The inversion operation projects each atom through the center of inversion, and across to the other side of the molecule.
Improper axis of rotation (Sn)
Rotation about n axis followed by inversion through center of symmetry
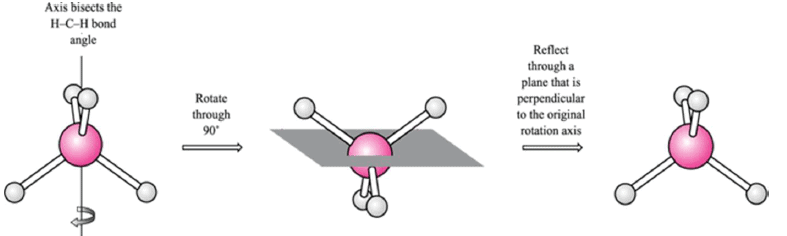
[Note that an S1 axis doesn’t exist; it is same as a mirror plane. Likewise, an S2 axis is a center of inversion].
Immediate applications of symmetry
1. Chirality: Molecules which lack symmetry are chiral and this property is called chirality which means “handedness”. Chiral objects can have two different forms, a right-handed and left-handed form which are mirror images of each other but are not exactly alike. The right-handed and left-handed forms of a chiral molecule make up a pair of stereoisomers called Enantiomers. When chiral organic compounds interact with living systems, the two enantiomers often interact very differently in terms of smell, taste and drug effects.
2. Optical activity: In general, if a molecule has improper rotation (Sn), then, it is optically inactive. This is because a molecule with an Sn is always superimposable on its mirror image.
3. Dipole Moment: If a molecule has a dipole moment, then, dipole must lie along the symmetry elements (lines, planes).
FAQs on Sawhorse formula into Newman projection formula- Stereochemistry
| 1. How do you convert a sawhorse formula into a Newman projection formula? |  |
| 2. What is the purpose of using a Newman projection formula? |  |
| 3. How can Newman projections help in understanding stereochemistry? |  |
| 4. Are there any limitations to using Newman projection formulas? |  |
| 5. Can I convert a Newman projection back into a sawhorse formula? |  |




















