Ex-3.2 Pair Of Linear Equations In Two Variables (Part - 2), Class 10, Math RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Q17. 2y-x = 9
6y-3x = 21
Sol. So we have 2y-x = 9 and 6y-3x = 21
Now, 2y-x = 9
= x = -9 + 2y
When y = 3 then, x = -3
When y = 4 then, x = -1
Thus, we have the following table giving points on the line 2y-x = 9
| X | -3 | -1 |
| Y | 3 | 4 |
Now, 6y-3x = 21
= x = 2y-7
When y = 2, then x = -3
When y = 3, then x = -1
Thus, we have the following table giving points on the line 6y-3x = 21
| X | -3 | -1 |
| Y | 2 | 3 |
Graph of the given equation

We find the lines represented by equations 2y-x = 9 and 6y-3x = 21 are parallel. So, the two lines have no common point.
Hence, the given system of equations is in-consistent.
Q18. 3x-4y-1 = 0
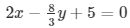
Sol. So we have 3x-4y-1 = 0 and 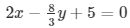
Now, 3x-4y-1 = 0
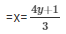
When y = 2 then, x = 3
When y = -1 then, x = -1
Thus, we have the following table giving points on the line 3x-4y-1 = 0
| X | -1 | 3 |
| Y | -1 | 2 |
Now, 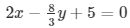
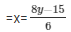
When y = 0, then x = -2.5
When y = 3, then x = 1.5
Thus, we have the following table giving points on the line 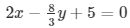
| X | -2.5 | 1.5 |
| Y | 0 | 3 |
Graph of the given equation
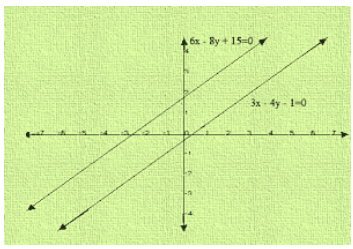
We find the lines represented by equations 3x-4y-1 = 0 and 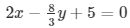
are parallel. So, the two lines have no common point.
Hence, the given system of equations is in-consistent.
Q19. Determine graphically the vertices of the triangle, the equations of whose sides are given below,
(i) 2y-x = 8, 5y-x = 14 and y-2x = 1
(ii) y = x, y = 0 and 3x + 3y = 10
Sol.
2y-x = 8
5y-x = 14
y-2x = 1
Now, 2y-x = 8
x = 2y-8
When y = 2 then x = -4
When y = 4 then x = 0
Thus, we have the following table giving points on the line 2y-x = 8
| X | -4 | 0 |
| y | 2 | 4 |
Now, 5y-x = 14
x = 5y-14
When y = 2, then x = 1
When y = 3 , then x = 1
Thus, we have the following table giving points on the line 5y-x = 14
| X | -4 | 1 |
| y | 2 | 3 |
We have,
y-2x = 1
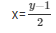
When y = -1, then x = 1
When y = 3 , then x = 1
Thus, we have the following table giving points on the line y-2x = 1
| X | -1 | 1 |
| y | 1 | 3 |
The graph of the given equation is:
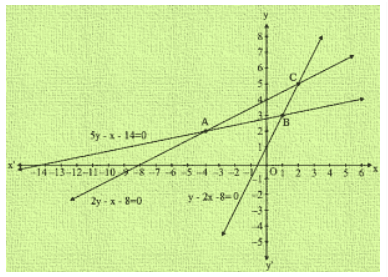
From the graph of the lines represent by the given equation, we observe that the lines taken in pairs intersect at points A(-4,2) B(1,3) and C(2,5)
Hence the vertices of the triangle are A(-4,2) B(1,3) and C(2,5)
The given systems of equations are:
y = x
y = 0
3x + 3y = 10
We have, y = x
When x = 1, then y = 1
When x = -2 , then y = -2
Thus, we have the following table giving points on the line y = x
| X | 1 | -2 |
| y | 73 | 43 |
The graph of the given equation is
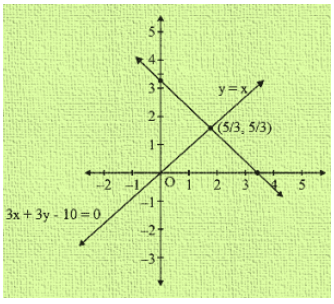
From the graph of the lines represent by the given equation, we observe that the lines taken in pairs intersect at points A(0,0) B(103,0) and C(53 53)
Hence the vertices of the triangle are A(0,0) B(103,0) and C(53 53)
Q20. Determine graphically whether the system of equations x-2y = 2 , 4x-2y = 5 is consistent or in-consistent
Sol. x-2y = 2
4x-2y = 5
Now, x-2y = 2
= > x = 2 + 2y
When y = 0 then, x = 2
When y = -1 then, x = 0
Thus, we have the following table giving points on the line x-2y = 2
| X | 2 | 0 |
| Y | 0 | -1 |
Now, 4x-2y = 5
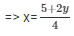
When y = 0, then x = 54
When y = 1, then x = 74
Thus, we have the following table giving points on the line 4x-2y = 5
| X | 54 | 74 |
| Y | 0 | 1 |
Graph of the given equation
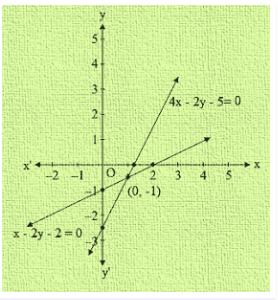
Clearly, the two lines intersect at (1,0)
Hence, the system of equation is consistent.
Q21. Determine by drawing graphs, whether the following system of linear equation has a unique solution or not:
(i)2x-3y = 6 and x + y = 1
(ii)2y = 4x-6 and 2x = y + 3
Sol.
(i) 2x-3y = 6 and x + y = 1
Now, 2x-3y = 6
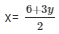
When y = 0 then, x = 3
When y = -2 then, x = 0
Thus, we have the following table giving points on the line 2x-3y = 6
| X | 3 | 0 |
| Y | 0 | -2 |
Now, x + y = 1
= > x = 1-y
When y = 0, then x = 1
When y = 1, then x = 0
Thus, we have the following table giving points on the line x + y = 1
| X | 0 | 1 |
| Y | 1 | 0 |
Graph of the given equations:
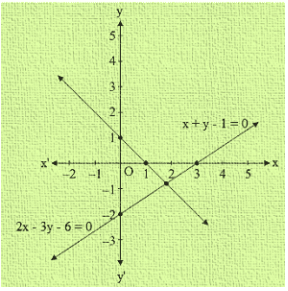
(ii) 2y = 4x-6
2x = y + 3
Now, 2y = 4x-6
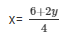
When y = -1 then, x = 1
When y = 5 then, x = 4
Thus, we have the following table giving points on the line 2y = 4x-6
| X | 1 | 4 |
| Y | -1 | 5 |
Now, 2x = y + 3
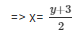
When y = 1, then x = 2
When y = 3, then x = 3
Thus, we have the following table giving points on the line 2x = y + 3
| X | 2 | 3 |
| Y | 1 | 3 |
Graph of the given equations:
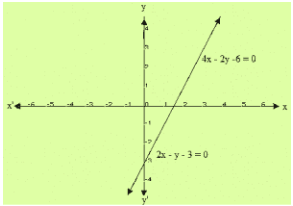
We find the graphs of the two equations are consistent.
Therefore, the system of equations has infinitely many solutions.
Q22. Solve graphically each of the following system of linear equations. Also, find the coordinates of the points where the lines meet axis of y.
(i) 2x-5y + 4 = 0 and 2x + y-8 = 0
(ii) 3x + 2y = 12 and 5x-2y = 4
(ii) 2x + y-11 = 0 and x-y-1 = 0
(iv) X + 2y-7 = 0 and 2x-y-4 = 0
(v) 3x + y-5 = 0 and 2x-y-5 = 0
(vi) 2x-y-5 = 0 and x-y-3 = 0
Sol.
(i) 2x-5y + 4 = 0 and 2x + y-8 = 0
Now, 2x-5y + 4 = 0
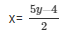
When y = 2 then, x = 3
When y = 4 then, x = 8
Thus, we have the following table giving points on the line2x-5y + 4 = 0
| X | 3 | 8 |
| Y | 2 | 4 |
Now, 2x + y-8 = 0
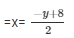
When y = 4, then x = 2
When y = 2, then x = 3
Thus, we have the following table giving points on the line 2x = y + 3
| X | 3 | 8 |
| Y | 2 | 4 |
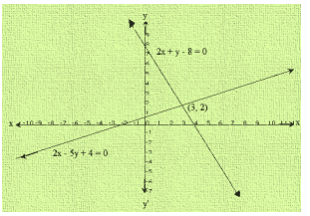
Clearly, two intersect at P(3,2)
Hence, x = 3 and y = 2 is the solution of the given system of equations.
We also observe that the lines represented by 2x-5y + 4 = 0 and 2x + y-8 = 0 meet y-axis at A(0, 45) and B(0,8) respectively.
(ii) 3x + 2y = 12 and 5x-2y = 4
Now, 3x + 2y = 12
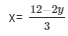
When y = 3 then, x = 2
When y = -3 then, x = 6
Thus, we have the following table giving points on the line 3x + 2y = 12
| X | 2 | 6 |
| Y | 3 | -3 |
Now, 5x-2y = 4
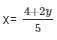
When y = 3, then x = 2
When y = -7, then x = -2
Thus, we have the following table giving points on the line 5x-2y = 4
| X | 2 | -2 |
| Y | 3 | -7 |
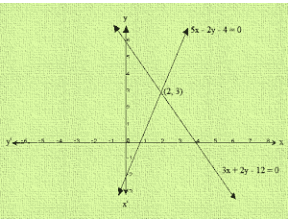
Clearly, two intersect at P(2,3)
Hence, x = 2 and y = 3 is the solution of the given system of equations.
We also observe that the lines represented by 3x + 2y = 12 and 5x-2y = 4 meet y-axis at A(0, 6) and B(0,-2) respectively.
(iii) 2x + y-11 = 0 and x-y-1 = 0
Now, 2x + y = 11
y = 11-2x
When y = 4 then, x = 3
When y = -5 then, x = 1
Thus, we have the following table giving points on the line 2x + y = 11
| X | 4 | 5 |
| Y | 3 | 1 |
Now, x-y = 1
= y = x-1
When x = 2, then y = 1
When y = 3, then y = 2
Thus, we have the following table giving points on the line x-y = 1
| X | 2 | 3 |
| Y | 1 | 2 |
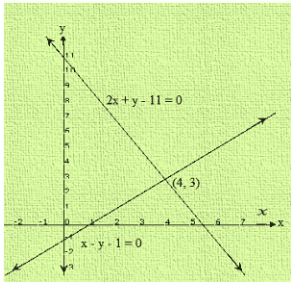
Clearly, two intersect at P (4, 3)
Hence, x = 4 and y = 3 is the solution of the given system of equations.
We also observe that the lines represented by 2x + y = 11 and x-y = 1 meet y-axis at A(0, 11) and B(0,-1) respectively.
(iv) x + 2y-7 = 0
2x-y-4 = 0
Sol.
Now, 2x-y-4 = 0
X = 7-2y
When y = 1 then, x = 5
When y = -2 then, x = 3
Thus, we have the following table giving points on the line 2x + y = 11
| X | 5 | 3 |
| Y | 1 | 2 |
Now, 2x-y-4 = 0
= y = 2x-4
When x = 2, then y = 0
When y = 0, then y = -4
Thus, we have the following table giving points on the line 2x-y-4 = 0
| X | 2 | 0 |
| Y | 0 | -4 |
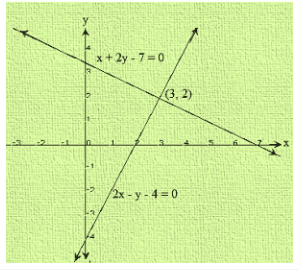
Clearly, two intersect at P (3,2)
Hence, x = 3 and y = 2 is the solution of the given system of equations.
We also observe that the lines meet y-axis at A(0, 3.5) and B(0,-4) respectively.
(v)3x + y-5 = 0 and 2x-y-5 = 0
Solution
Now, 3x + y-5 = 0
y = 5-3x
When x = 1 then, y = 2
When x = 2 then, y = -1
Thus, we have the following table giving points on the line 3x + y-5 = 0
| X | 1 | 2 |
| Y | 2 | -1 |
Now, 2x-y-5 = 0
= y = 2x-5
When x = 0, then y = -5
When x = 2, then y = -1
Thus, we have the following table giving points on the line 2x-y-5 = 0
| X | 0 | 2 |
| Y | -5 | -1 |
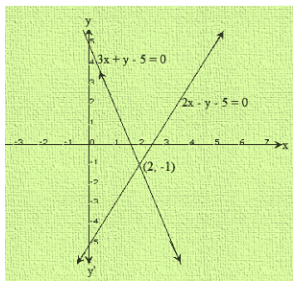
Clearly, two intersect at P (2,-1)
Hence, x = 2 and y = -1 is the solution of the given system of equations.
We also observe that the lines meet y-axis at A(0,5) and B(0,-5) respectively.
(vi)2x-y-5 = 0 and x-y-3 = 0
Now, 2x-y-5 = 0
y = 2x-5
When x = 1 then, y = -3
When x = 2 then, y = -1
Thus, we have the following table giving points on the line 2x-y-5 = 0
| X | 1 | 2 |
| Y | -3 | -1 |
Now, x-y-3 = 0
= y = x-3
When x = 3, then y = 0
When x = 4, then y = -1
Thus, we have the following table giving points on the line x-y-3 = 0
| X | 3 | 0 |
| Y | 4 | -1 |
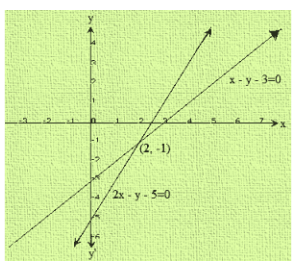
Clearly, two intersect at P(2,-1)
Hence, x = 2 and y = -1 is the solution of the given system of equations.
We also observe that the lines meet y-axis at A(0,5) and B(0,-3) respectively.
Q23. Solve the following system of linear equations graphically and shade the region between the two lines and x- axis.
(i) 2x + 3y = 12 and x-y = 1
(ii) 3x + 2y-4 = 0 and 2x-3y-7 = 0
(iii) 3x + 2y-11 = 0 and 2x-3y + 10 = 0
Sol. (i) 2x + 3y = 12 and x-y = 1
The system of the given equation is y = x, 3y = x and y + x = 8
Now, 2x + 3y = 12
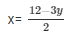
When y = 2, then x = 3
When y = 4, then x = 0
Thus, we have the following table:
| X | 0 | 3 |
| Y | 4 | 2 |
We have,
x-y = 1
x = y + 1
When y = 0, then x = 1
When y = 1, then x = 2
Thus, we have the following table:
| X | 1 | 2 |
| Y | 0 | 1 |
Graph of the given system is:
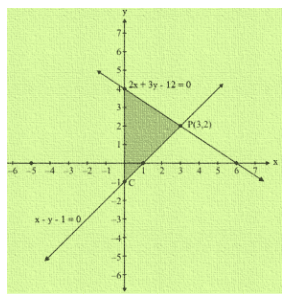
Clearly the two lines intersect at P (3, 2)
Hence x = 3 and y = 2 is the solution of the given system of equations.
(ii) 3x + 2y-4 = 0 and 2x-3y-7 = 0
The system of the given equation is 3x + 2y-4 = 0 and 2x-3y-7 = 0
Now,3x + 2y-4 = 0
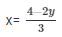
When y = 5, then x = -2
When y = 8, then x = -4
Thus, we have the following table:
| X | -2 | -4 |
| Y | 5 | 8 |
We have,
2x-3y-7 = 0
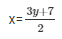
When y = 1, then x = 5
When y = -1, then x = 2
Thus, we have the following table:
| X | 5 | 2 |
| Y | 1 | -1 |
Graph of the given system is:
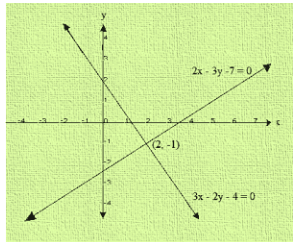
Clearly the two lines intersect at P(2,-1)
Hence x = 2 and y = -1 is the solution of the given system of equations.
(iii) 3x + 2y-11 = 0 and 2x-3y + 10 = 0
Now,3x + 2y-11 = 0
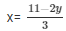
When y = 1, then x = -3
When y = 4, then x = 1
Thus, we have the following table:
| X | 3 | 1 |
| Y | 1 | 4 |
We have,
2x-3y + 10 = 0

When y = 0, then x = -5
When y = 2, then x = -2
Thus, we have the following table:
| X | -5 | -2 |
| Y | 0 | 2 |
Graph of the given system is:
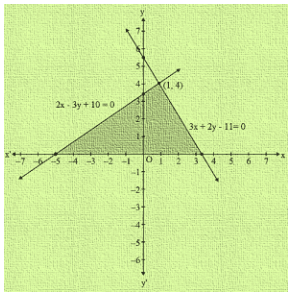
Clearly the two lines intersect at P(1,4)
Hence x = 1 and y = 4 is the solution of the given system of equations.
Q24. Draw the graphs of the following equations on the same graph paper:
2x + 3y = 12 and x-y = 1
Sol. Now,2x + 3y = 12
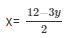
When y = 0, then x = 6
When y = 2, then x = 3
Thus, we have the following table:
| X | 6 | 3 |
| Y | 0 | 2 |
We have,
x-y = 1
x = 1 + y
When y = 0, then x = 1
When y = -1, then x = 0
Thus, we have the following table:
| X | 1 | 0 |
| Y | 0 | -1 |
Graph of the given system is:
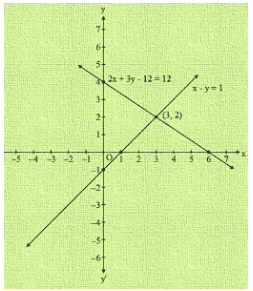
Clearly the two lines intersect at A(3,2)
We also observe that the lines meet y-axis B(0,-1) and C(0,4)
Hence the vertices of the required triangle are A(3,2) , B(0,-1) and C(0,4).
Q25. Draw the graphs of x-y + 1 = 0 and 3x + 2y-12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and x-axis and shade the triangular area. Calculate the area bounded by these lines and x- axis.
Sol. The given system of equations is:
x-y + 1 = 0 and 3x + 2y-12 = 0
Now, x-y + 1 = 0
x = y-1
When y = 3, then x = 2
When y = -1, then x = -2
Thus, we have the following table:
| X | 2 | -2 |
| Y | 3 | -1 |
We have,
3x + 2y-12 = 0
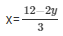
When y = 6, then x = 0
When y = 3, then x = 2
Thus, we have the following table:
| X | 0 | 2 |
| Y | 6 | 3 |
Graph of the given system is:
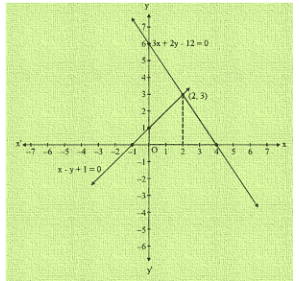
Clearly, the two lines intersect at A(2,3)
We also observe that the lines meet x-axis B(-1,0) and C(4,0)
Thus x = 2 and y = 3 is the solution of the given system of equations.
AD is drawn perpendicular A on x-axis. Clearly we have,
AD = y-coordinate point A (2,3)
AD = 3 and BC = 4-(-1) = 4 + 1 = 5
|
5 videos|292 docs|59 tests
|
FAQs on Ex-3.2 Pair Of Linear Equations In Two Variables (Part - 2), Class 10, Math RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. What are pair of linear equations in two variables? |  |
| 2. How can we solve a pair of linear equations in two variables? |  |
| 3. What is the importance of solving pair of linear equations in two variables? |  |
| 4. Can a pair of linear equations in two variables have more than one solution? |  |
| 5. How can we verify the solution of a pair of linear equations in two variables? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















