Ex-3.3 Pair Of Linear Equations In Two Variables (Part - 1), Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Solve the following system of equations:
Question 1: 11x + 15y + 23 = 0 and 7x – 2y – 20 = 0
Sol. The given system of equation is
11x + 15y + 23 = 0 …………………………. (i)
7x − 2y − 20 = 0 ………………………………..(ii)
From (ii)
2y = 7x − 20
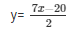 ……………………………… (iii)
……………………………… (iii)
Substituting the value of y in equation (i) we get,
= 11x + 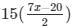 + 23 = 0
+ 23 = 0
= 11x + 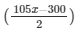 + 23 = 0
+ 23 = 0
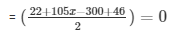
= 127x = 254 = x = 2
Putting the value of x in the equation (iii)
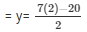
y = − 3
The value of x and y are 2 and − 3 respectively.
Question 2: 3x – 7y + 10 = 0, y – 2x – 3 = 0
Sol. The given system of equation is
3x − 7y + 10 = 0 …………………………. (i)
y − 2x − 3 = 0 ………………………………..(ii)
From (ii)
y − 2x − 3 = 0
y = 2x + 3 ……………………………… (iii)
Substituting the value of y in equation (i) we get,
= 3x − 7(2x + 3) + 10 = 0
= 3x + 14x − 21 + 10 = 0
= − 11x = 11
= x = − 1
Putting the value of x in the equation (iii)
= y = 2( − 1) + 3
y = 1
The value of x and y are − 1 and 1 respectively.
Question 3: 0.4x + 0.3y = 1.7, 0.7x – 0.2y = 0.8
Sol. The given system of equation is
0.4x + 0.3y = 1.7
0.7x − 0.2y = 0.8
Multiplying both sides by 10
4x + 3y = 17 ……………………….. (i)
7x − 2y = 8 …………………………… (ii)
From (ii)
7x − 2y = 8
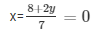 ……………………………… (iii)
……………………………… (iii)
Substituting the value of y in equation (i) we get,
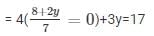
= 32 + 29y = 119
= 29y = 87
= y = 3
Putting the value of y in the equation (iii)
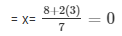
= x = 14/7 = 0
= x = 2
The value of x and y are 2 and 3 respectively.
Question 4. x/2 + y = 0.8
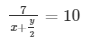
Sol. The given system of equation is
x/2 + y = 0.8
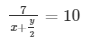
Therefore x + 2y = 1.6
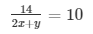
x + 2y = 1.6
7 = 10x + 5y
Multiplying both sides by 10
10x + 20y = 16 ……………………….. (i)
10x + 5y = 7 …………………………… (ii)
Subtracting two equations we get,
15y = 9
y = 35
x = 1.6 − 2(3/5)
= 1.6 − (6/5)
= 2/5
The value of x and y are 2/5 and3/5 respectively.
Question 5. 7(y + 3) − 2(x + 3) = 14
4(y − 2) + 3(x − 3) = 2
Sol. The given system of equation is
7(y + 3) − 2(x + 3) = 14…………………………. (i)
4(y − 2) + 3(x − 3) = 2………………………………..(ii)
From (i)
7y + 21 − 2x − 4 = 14
7y = 14 + 4 − 21 + 2x
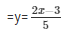
From (ii)
= 4y − 8 + 3x − 9 = 2
= 4y + 3x − 17 − 2 = 0
= 4y + 3x − 19 = 0 ……………..(iii)
Substituting the value of y in equation (iii)
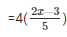 + 3x − 19 = 0
+ 3x − 19 = 0
= 8x − 12 + 21x − 133 = 0
= 29x = 145
= x = 5
Putting the value of x in the above equation
= y = 1
The value of x and y are 5 and 1 respectively.
Question 6
x/7 + y/3 = 5
x/2 − y/9 = 6
Sol. The given system of equation is
x/7 + y/3 = 5…………………………. (i)
x/2 − y/9 = 6………………………………..(ii)
From (i)
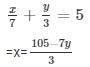
From (ii)
x/2 − y/9 = 6
= 9x − 2y = 108 ………………………(iii)
Substituting the value of x in equation (iii) we get,
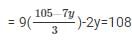
= 945 − 63y − 6y = 324
= 945 − 324 = 69y
= 69y = 621
= y = 9
Putting the value of y in the above equation
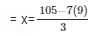
y = 14
The value of x and y are 5 and 14 respectively.
Question 7
x/3 + y/4 = 11
5x/6 − y/3 = − 7
Sol. The given system of equation is
x/3 + y/4 = 11…………………………. (i)
5x/6 − y/3 = − 7………………………………..(ii)
From (i)
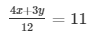
= 4x + 3y = 132……………………(iii)
From (ii)
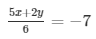
= 5x − 2y = − 42 ………………………(iv)
Let us eliminate y from the given equations. The co efficient of y in the equation (iii) and (iv) are 3 and 2 respectively. The L.C.M of 3 and 2 is 6. So, we make the coefficient of y equal to 6 in the two equations.
Multiplying equation (iii)*2 and (iv)*3 we get
= 8x + 6y = 264 ……………………..(v)
= 15x − 6y = − 126 ………………………(vi)
Adding equation (v) and (vi)
8x + 15x = 264 − 126
= 23x = 138
x = 6
Putting the value of x in the equation (iii)
= 24 + 3y = 132
= 3y = 108
y = 36
The value of x and y are 36 and 6 respectively.
Question 8. 4/x + 3y = 8
6/x − 4y = − 5
Sol. taking1/x = u
The new equation becomes
4u + 3y = 8……………………(i)
6u − 4y = − 5…………………….(ii)
From (i)
4u = 8 − 3y
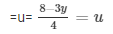
From (ii)
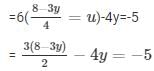
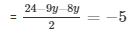
= 24 − 17y = − 10
= − 17y = − 34
= y = 2
Putting y = 2 in 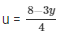 = u we get ,
= u we get ,
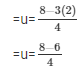
= u = 2/4
= x = u = 2
So the Solution of the given system of equation is x = 2 and y = 2
Question 9. x + y/2 = 4
2/y + x/3 = 5
Sol. The given system of equation is:
x + y/2 = 4 …………………….(i)
2/y + x/3 = 5…………………….(ii)
From (i) we get,
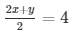
= 2x + y = 8
= y = 8 − 2x
From (ii) we get,
x + 6y = 15 ………………(iii)
Substituting y = 8 − 2x in (iii) , we get
= x + 6(8 − 2x) = 15
= x + 48 − 12x = 15
= − 11x = 15 − 48
= − 11x = − 33
= x = 3
Putting x = 3 in y 8 − 2x, we get
y = 8 − (2*3)
= y = 8 − 6 = 2
The Solution of the given system of equation are x = 3 and y = 2 respectively.
Question 10. x + 2y = 3/2
2x + y = 3/2
Sol. The given system of equation is
x + 2y = 3/2 ………………….(i)
2x + y = 3/2……………………(ii)
Let us eliminate y from the given equations. The coefficients of y in the given equations are 2 and 1 respectively. The L.C.M of 2 and 1 is 2. So, we make the coefficient of y equal to 2 in the two equations.
Multiplying equation (i)*1 and (ii)*2
x + 2y = 3/2 ……………………….(iii)
4x + 2y = 3 …………………………………………………….(iv)
Subtracting equation (iii) from (iv)
4x − x + 2y − 2y = 3 − x + 2y = 3/2
= 3x = x + 2y = 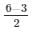
= 3x = 3/2
= x = 1/2
Putting x = 1/2 in equation (iv)
4(1/2) + 2y = 3
= 2 + 2y = 3
= y = 1/2
The Solution of the system of equation is x = 1/2 and y = 1/2
Question 11. √2x + √3y = 0
√3x − 8–√y = 0
Sol. √2x + √3y = 0………………………..(i)
√3x − 8–√y = 0………………………..(ii)
From equation (i)
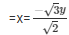 ……………..(iii)
……………..(iii)
Substituting this value in equation (ii) we obtain
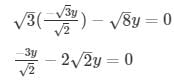
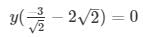
= y = 0
Substituting the value of y in equation (iii) we obtain
= x = 0
The value of x and y are 0 and 0 respectively.
Question 12. 3x − 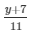 + 2 = 10
+ 2 = 10
2y − 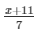 = 10
= 10
Sol. The given system of equation is:
3x − 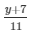 + 2 = 10 ………………..(i)
+ 2 = 10 ………………..(i)
2y − 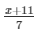 = 10……………………..(ii)
= 10……………………..(ii)
From equation (i)
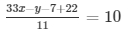
= 33x − y + 15 = 110
= 33x + 15 − 110 = y
= y = 33x − 95
From equation (ii)
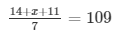
= 14y + x + 11 = 70
= 14y + x = 70 − 11
= 14y + x = 59 ……………………..(iii)
Substituting y = 33x − 95 in (iii) we get,
14(33x − 95) + x = 59
= 462x − 1330 + x = 59
= 463x = 1389
= x = 3
Putting x = 3 in y = 33x − 95 we get,
= y = 33(3) − 95
= 99 − 95 = 4
The Solution of the given system of equation is 3 and 4 respectively.
Question 13. 2x − 3/y = 9
3x + 7/y = 2
Sol. 2x − 3/y = 9……………………………. (i)
3x + 7/y = 2…………………………… (ii)
Taking 1y = u the given equation becomes,
2x − 3u = 9 ………………………..(iii)
3x + 7u = 2………………………..(iv)
From (iii)
2x = 9 + 3u
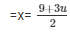
Substituting the value x = 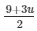 in equation (iv) we get,
in equation (iv) we get,
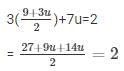
= 27 + 23u = 4
= u = − 1
= y = 1/u = − 1
Putting u = − 1 in = x = 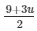 we get,
we get,
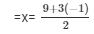
= x = 3
The Solution of the given system of equation is 3 and − 1 respectively.
Question 14. 0.5x + 0.7y = 0.74
0.3x + 0.5y = 0.5
Sol. The given system of equation is
0.5x + 0.7y = 0.74………………………(i)
0.3x − 0.5y = 0.5 …………………………..(ii)
Multiplying both sides by 100
50x + 70y = 74 ……………………….. (iii)
30x + 50y = 50 …………………………… (iv)
From (iii)
50x = 74 − 70y
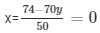 ……………………………… (iii)
……………………………… (iii)
Substituting the value of y in equation (iv) we get,
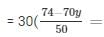 0) + 50y = 50
0) + 50y = 50
= 222 − 210y + 250y = 250
= 40y = 28
= y = 0.7
Putting the value of y in the equation (iii)
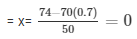
= x = 25/50 = 0
= x = 0.5
The value of x and y are 0.5 and 0.7 respectively.
Question 15. 1/7x + 1/6y = 3
1/2x − 1/3y = 5
Sol. 1/7x + 1/6y = 3 ………………………….. (i)
1/2x − 1/3y = 5……………………………. (ii)
Multiplying (ii) by 1/2 we get,
1/4x − 1/6y = 5/2……………………………. (iii)
Solving equation (i) and (iii)
1/7x + 1/6y = 3 ………………………….. (i)
1/4x − 1/6y = 5/2 ……………………………. (iii)
Adding we get,
1/7x + 1/6y = 3 + 5/2
= x = 1/14
When, x = 1/14 we get,
Using equation (i)

= 1/6y = 1
= y = 1/6
The Solution of the given system of equation is x = 1/14 and y = 1/6 respectively.
Question 16. 1/2x + 1/3y = 2
1/3x + 1/2y = 13/6
Sol. Let 1/x = u
Let 1/y = v
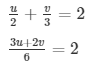
3u + 2v = 12 ……………………..(i)
And, u/3 + v/2 = frac136
= v = 3
1/u = x = 1/21/v = y = 1/3
|
5 videos|292 docs|59 tests
|
FAQs on Ex-3.3 Pair Of Linear Equations In Two Variables (Part - 1), Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. What are pair of linear equations in two variables? |  |
| 2. How can we solve a pair of linear equations in two variables? |  |
| 3. What is the graphical method to solve a pair of linear equations in two variables? |  |
| 4. Explain the substitution method to solve a pair of linear equations in two variables. |  |
| 5. How does the elimination method work to solve a pair of linear equations in two variables? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















