Ex-3.3 Pair Of Linear Equations In Two Variables (Part - 2), Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Question 17. 15/u + 2/v = 1/7
1/u + 1/v = 36/5
Sol. Let 1/x = u
Let 1/y = v
15x + 2y = 17 …………………………..(i)
x + y = 36/5……………………….(ii)
From equation (i) we get ,
2y = 17 − 15x
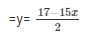
Substituting y = 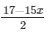 in equation (ii) we get,
in equation (ii) we get,
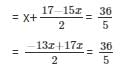
= 5( − 13x + 17) = 72
= − 65x = − 13
= x = 1/5
Putting x = 1/5 in equation (ii) , we get
1/5 + y = 36/5
= y = 7
= v = 1/y = 1/7
The Solution of the given system of equation is 5 and 1/7 respectively.
Question 18. 3/x − 1/y = − 9
2/x + 1/y = 5
Sol. Let 1/x = u
Let 1/y = v
3u − v = − 9…………………..(i)
2u + 3v = 5 ……………………….(ii)
Multiplying equation (i) *3 and (ii) *1 we get,
9u − 3v = − 27 ………………………….. (iii)
2u + 3v = 5 ……………………………… (iv)
Adding equation (i) and equation (iv) we get ,
9u + 2u − 3v + 3v = − 27 + 5
= u = − 2
Putting u = − 2 in equation (iv) we get,
2( − 2) + 3v = 5
= 3v = 9
= v = 3
Hence x = 1/u = − 1/2
Hence y = 1/v = 1/3
Question 19. 2/x − 3/y = 9/xy
2/x + 1/y = 9/xy
Sol. 2/x − 3/y = 9/xy ……………………… (i)
2/x + 1/y = 9/xy…………………….. (ii)
Multiplying equation (i) adding equation (ii) we get,
2y + 3x = 9………………………..(iii)
4y + 9x = 21 ……………………….(iv)
From (iii) we get ,
3x = 9 − 2y
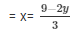
Substituting x = 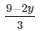 in equation (iv) we get
in equation (iv) we get
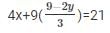
= 4y + 3(9 − 2y) = 21
= − 2y = 21 − 27
= y = 3
Putting y = 3 in x = 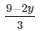 we get,
we get,
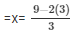
= x = 1
Hence the Solutions of the system of equation are 1 and 3 respectively.
Question 20. 1/5x + 1/6y = 1/2
1/5x + 1/6y = 8
Sol. Let 1/x = u
Let 1/y = v
u/5 + v/6 = 12
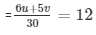
= 6u + 5v = 360 …………….(i)
u/3 + 3v/7 = 8
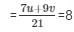
= 7u − 9v = 168 …………….(ii)
Let us eliminate v from the equation (i) and (ii) . multiplying equation (i) by 9 and (ii) by 5
54u + 35u = 3240 + 840
89u = 4080
= u = 4080/89
Putting u = 4080/89 in equation (i) we get,
6(4080/89) + 5v = 360
= 24480/89 + 5v = 360
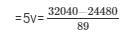
= v = 7560/89
= v = 7560/5∗89
= v = 1512/89
1/u = x = 89/4080
1/v = y = 89/1512
.
Question 27.
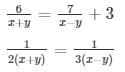
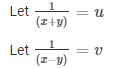
Then, the given system of equation becomes,
6u = 7v + 3
6u − 7v = 3……………………….. (i)
And u/2 = v/3
3u = 2v
3u − 2v = 0 ……………………… (ii)
Multiplying equation (ii) by 2 and (i) 1
6u − 7v = 3
6u − 4v = 0
Subtracting v = − 1 in equation (ii) ,we get
3u − 2( − 1) = 0
3u + 2 = 0
3u = − 2
= u = − 2/3
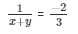
x + y = − 3/2 …………………….(v)
and v = − 1
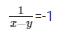
x − y = − 1……………………(vi)
Adding equation (v) and equation (vi) we get,
2x = − 3/2 − 1
= x = − 5/4
Putting x = − 2/3 in equation (vi)
= − 5/4 − y = − 1
= y = − 1/4
Question 28
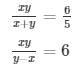
Sol.
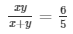
5xy = 6(x + y)
= 5xy = 6x + 6y ……………….(i)
And
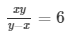
xy = 6(y − x)
= xy = 6y − 6x ……………………(ii)
Adding equation (i) and equation (ii) we get,
6xy = 6y + 6y
6xy = 12y
x = 2
Putting x = 2 in equation (i) we get,
10y = 12 + 6y
10 − 6y = 12
4y = 12
y = 3
The Solution of the given system of equation is 2 and 3 respectively.
Question 29
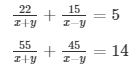
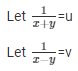
Sol. Then the given system of equation becomes:
22u + 45v = 5 ……………………….. (i)
55u + 45v = 14 ………………………(ii)
Multiplying equation (i)by 3 and (ii) by 1
66u + 45v = 15 ……………………… (iii)
55u + 45v = 14 ……………………… (iv)
Subtracting equation (iv) from equation (iii) , we get
66u − 55u = 15 − 14
= 11u = 1
= u = 1/11
Putting = u = 1/11 in equation (i) we get,
= 2 + 15v = 5
= 15v = 3
= v = 15
Now,
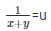
= x + y = 11 ……………..(v)
1/x − y = v
= x − y = 5 …………………..(vi)
Adding equation (v) and (vi) we get,
2x = 16
= x = 8
Putting the value of x in equation (v)
8 + y = 11
= y = 3
The Solutions of the given system of equation are 8 and 3 respectively.
Question 30
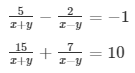
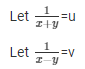
Sol.
Then the given system of equation becomes:
5u − 2v = − 1 ……………………….. (i)
15u + 7v = 10 ………………………(ii)
Multiplying equation (i) by 7 and (ii) by 2
35u − 14v = − 7 ……………………… (iii)
30u + 14v = 20 ……………………… (iv)
Subtracting equation (iv) from equation (iii) , we get
− 2v = − 1 − 1
= − 2v = − 2
= v = 1
Now,
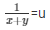
= x + y = 5 ……………..(v)
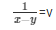
= x − y = 1 …………………..(vi)
Adding equation (v) and (vi) we get,
2x = 6
= x = 3
Putting the value of x in equation (v)
3 + y = 5
= y = 2
The Solutions of the given system of equation are 3 and 2 respectively.
Question 31.
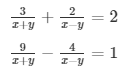
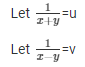
Sol.Then the given system of equation becomes:
3u + 2v = 2 ……………………….. (i)
9u + 4v = 1 ………………………(ii)
Multiplying equation (i) by 3 and (ii) by 1
6u + 4v = 4 ……………………… (iii)
9u − 4v = 1 ……………………… (iv)
Adding equation (iii) and (iv) we get,
45u = 5
= u = 3
Subtracting equation (iv) from equation (iii) , we get
2v = 2 − 1
= 2v = 1
= v = 1/2
Now,
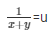
= x + y = 3 ……………..(v)
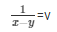
= x − y = 2 …………………..(vi)
Adding equation (v) and (vi) we get,
2x = 5
= x = 5/2
Putting the value of x in equation (v)
5/2 + y = 11
= y = 1/2
The Solutions of the given system of equation are 5/2 and 1/2 respectively.
Question 32
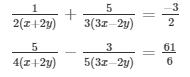
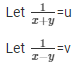
Sol. Then the given system of equation becomes:
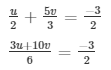
3u + 10v = − 9 ………………………..(i)
5u/4 − 3v/5 = 61/60
25u − 12v = 61/3 ………………………(ii)
Multiplying equation (i) by 12 and (ii) by 10
36u + 120v = − 108 ……………………… (iii)
250u + 120v = 610/3 ……………………… (iv)
Adding equation (iv) and equation (iii) , we get
36u + 250u = 610/3 − 108
= 286u = 286/3
= u = 1/3
Putting u = 61/3 in equation (i)
3(1/3) + 10v = − 9
= v = − 1
Now,
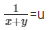
= x + 2y = 3 ……………..(v)
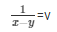
= 3x − 2y = − 1 …………………..(vi)
Putting x = 1/2 in equation (v) we get,
1/2 + 2y = 3
= y = 5/4
The Solutions of the given system of equation are 1/2
And 5/4 respectively.
|
5 videos|292 docs|59 tests
|
FAQs on Ex-3.3 Pair Of Linear Equations In Two Variables (Part - 2), Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. How can I solve a pair of linear equations in two variables using the RD Sharma Solutions? |  |
| 2. What are the different methods to solve a pair of linear equations in two variables? |  |
| 3. How can I verify the solution of a pair of linear equations in two variables? |  |
| 4. How can I apply the substitution method to solve a pair of linear equations in two variables? |  |
| 5. How can I apply the elimination method to solve a pair of linear equations in two variables? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|

















