Ex-3.4 Pair Of Linear Equations In Two Variables, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Q.1: x + 2y + 1 = 0 and 2x – 3y – 12 = 0
Sol.
x + 2y + 1 = 0 …………………………………….(i)
2x-3y-12 = 0………………………………….. (ii)
Here a1 = 1 , b1 = 2 , c1 = 1
a2 = 2 , b2 = -3 , c2 = -12
By cross multiplication method,
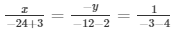
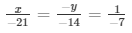
Now,
x /− 21 = 1 /− 7
= x = 3
And,
− y /− 14 = 1 /− 7
= y = -2
The solution of the given system of equation is 3 and -2 respectively.
Q.2: 3x + 2y + 25 = 0, 2x + y + 10 = 0
Sol. 3x + 2y + 25 = 0 …………………………………….(i)
2x + y + 10 = 0………………………………….. (ii)
Here a1 = 3 , b1 = 2 , c1 = 25
a2 = 2 , b2 = 1 , c2 = 10
By cross multiplication method,
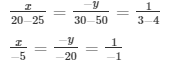
Now,
x/ − 5 = 1 /− 1
= x = 5
And,
− y /− 20 = 1/ − 1
= y = -20
The solution of the given system of equation is 5 and -20 respectively.
Q.3: 2x + y = 35, 3x + 4y = 65
Sol. 2x + y = 35 ……………………………….(i)
3x + 4y = 65…………………………….. (ii)
Here a1 = 2 , b1 = 1 , c1 = 35
a2 = 3 , b2 = 4 , c2 = 65
By cross multiplication method,
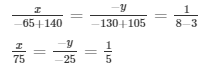
Now,
x/75 = 1/5
= x = 15
And,
− y /− 25 = 1/5
= y = 5
The solution of the given system of equation is 15 and 5 respectively.
Q.4: 2x – y – 6 = 0, x – y – 2 = 0
Sol. 2x-y = 6 ……………………………….(i)
x-y = 2…………………………….. (ii)
Here a1 = 2 , b1 = -1 , c1 = 6
a2 = 1 , b2 = -1 , c2 = 2
By cross multiplication method,
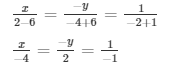
Now,
x/ − 4 = 1/ − 1
= x = 4
And,
− y/2 = 1 /− 1
= y = 2
The solution of the given system of equation is 4 and 2 respectively.
Q5: 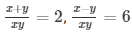
Sol. 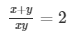
= 1/x + 1/y = 2 ……………………………….. (i)
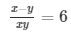
= 1/x − 1/y = 6 ………………………………… (ii)
Taking 1/x = u
Taking 1/y = v
= u + v = 2 …………………………… (iii)
= u-v = 6 ……………………………. (iv)
By cross multiplication method,

Now,
u/4 = 1/ − 2
= u = -2
And,
− v/ − 8 = 1/ − 2
= v = 4
1/u = x = − 1/2
1/v = y = 1/4
The solution of the given system of equation is − 1/2 and 1/4 respectively.
Q.6: ax + by = a-b, bx-ay = a + b
Sol. ax + by = a-b……………………………….(i)
bx-ay = a + b…………………………….. (ii)
Here a1 = a , b1 = b , c1 = a-b
a2 = b , b2 = -a , c2 = a + b
By cross multiplication method,
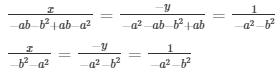
Now,
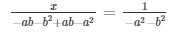
= x = 1
And,
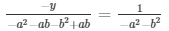
= y = -1
The solution of the given system of equation is 1 and -1 respectively.
Q.7: x + ay-b = 0, ax-by-c = 0
Sol. x + ay-b = 0 ……………………………….. (i)
ax-by-c = 0………………………………. (ii)
Here a1 = 1 , b1 = a , c1 = -b
a2 = a , b2 = -b , c2 = -c
By cross multiplication method,

Now,
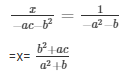
And,
The solution of the given system of equation is  respectively.
respectively.
Q8 ax + by = a2
bx + ay = b2
Sol. ax + by = a2……………………………….(i)
bx + ay = b2…………………………….. (ii)
Here a1 = a , b1 = b , c1 = a2
a2 = b , b2 = a , c2 = b2
By cross multiplication method,

Now,
And,
The solution of the given system of equation is  respectively.
respectively.
Q9
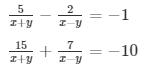
Sol.
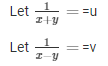
The given system of equations are :
5u-2v = -1
15u + 7v = 10
Here a1 = 5, b1 = -2 , c1 = 1
a2 = 15 , b2 = 7 , c2 = -10
By cross multiplication method,
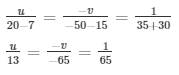
Now,
u/13 = 1 /− 65
= u = 1/5
1/u = = x + y
= x + y = 5 ………………………..(i)
And,
− v / − 65 = 1/ − 65
= v = 1
1v = = x-y
= x-y = 1 ………………………… (ii)
Adding equation (i) and (ii)
2x = 6
= x = 3
Putting the value of x in equation (i)
3 + y = 5
= y = 2
The solution of the given system of equation is 3 and 2 respectively.
Q10
2/x + 3/y = 13
5/x − 4/y = − 2
Sol.
Let 1/x = u
Let 1/y = v
The given system of equations becomes:
2u + 3v = 13 ……………………………… (i)
5u-4v = -2…………………………………. (ii)
By cross multiplication method,
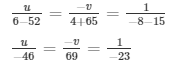
Now,
u /− 46 = 1/ − 23
= u = 2
1/u = = 1/x
= x = 12
And,
− v/69 = 1 /− 23
= v = 3
1/v = 1/y
= y = 13
The solutions of the given system of equations are 1/2 and 1/3 respectively.
Q11
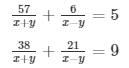
Sol.
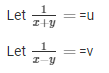
The given system of equations are :
57u + 6v = 5
38u + 21v = 9
Here a1 = 57, b1 = 6 , c1 = -5
a2 = 38 , b2 = 21 , c2 = -9
By cross multiplication method,
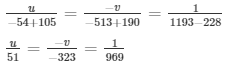
Now,
u/51 = 1/969
= u = 1/19
1/u = x + y
= x + y = 19 ………………………..(i)
And,
− v/ − 323 = 1/969
= v = 1/3
1/v = = x-y
= x-y = 3 ………………………… (ii)
Adding equation (i) and (ii)
2x = 22
= x = 11
Putting the value of x in equation (i)
11 + y = 19
= y = 8
The solution of the given system of equation is 11 and 8 respectively.
Q12
x/a − y/b = 2
ax-by = a2-b2
Sol.
a1 = 1/a , Let b1 = 1/b, Let c1 = -2
a2 = a , b2 = -b, c2 = b2-a2
By cross multiplication method
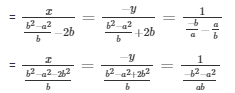
Now, 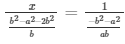
x = a
and, 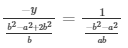
= y = b
Hence the solution of the given system of equation are a and b respectively.
Q13
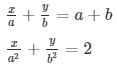
Sol.
Here, a1 = 1/a , Let b1 = 1/b, Let c1 = -(a + b)
a2 = 1/a2, b2 = 1/b2, c2 = -2
By cross multiplication method
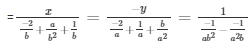
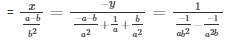
Now, 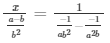
= x = a2
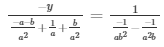
= y = b2
The solution of the given system of equation are a2 and b2 respectively.
Q14
x/a = y/b
ax + by = a2 + b2
Sol. Here, a1 = 1a , Let b1 = 1b, c1 = 0
Here, a1 = a , b2 = b, Let c1 = -(a2 + b2)
By cross multiplication method

Now, 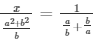
= x = a
And 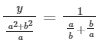
= y = b
The solution of the given system of equations are a and b respectively.
Q15
2ax + 3by = a + 2b
3ax + 2by = 2a + b
Sol. The given system of equation is
2ax + 3by = a + 2b …………………………… (i)
3ax + 2by = 2a + b…………………………….. (ii)
Here a1 = 2a, b1 = 3b , c1 = -(a + 2b)
a2 = 3a , b2 = 2b , c2 = -(2a + b)
By cross multiplication method
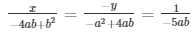
Now,
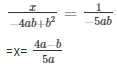
And, 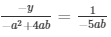
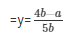
The solutions of the system of equations are 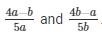
Q16
5ax + 6by = 28
3ax + 4by = 18
Sol.
The systems of equations are:
5ax + 6by = 28 …………………………. (i)
3ax + 4by = 18……………………………. (ii)
Here a1 = 5a, b1 = 6b , c1 = -(28)
a2 = 3a , b2 = 4b , c2 = -(18)
By cross multiplication method
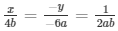
Now,
x/4b = 1/2ab
= x = 2a
And, − y/ − 6a = 1/2ab
= y = 3/b
The solution of the given system of equation is 2/a and 3/b.
Q17
(a + 2b)x + (2a-b)y = 2
(a-2b)x + (2a + b)y = 3
Soln.
The given system of equations are :
(a + 2b)x + (2a-b)y = 2 ………………………. (i)
(a-2b)x + (2a + b)y = 3………………………….. (ii)
Here a1 = a + 2b, b1 = 2a-b , c1 = -(2)
a2 = a-2b , b2 = 2a + b , c2 = -(3)
By cross multiplication method:
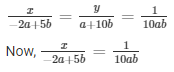
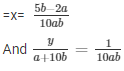
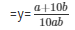
The solution of the system of equations are = x = 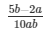
And = y = 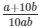 respectively.
respectively.
Q18
x + y = 2a2
Sol. The given systems of equations are:
x + y = 2a2
From equation (i)
From equation (ii)
X + y-2a2 = 0
Here 
a2 = 1, b2 = 1 , c2 = -2a2
By cross multiplication method:
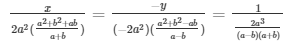
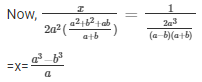
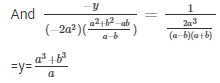
The solutions of the given system of equations are 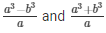 respectively.
respectively.
Q19
bx + cy = a + b
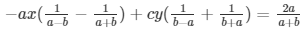
Sol. The system of equation is given by :
bx + cy = a + b ……………………………………. (i)
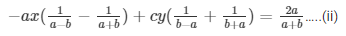
From equation (i)
bx + cy-(a + b) = 0
From equation (ii)
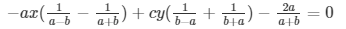
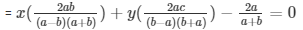
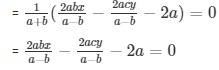
= 2abx-2acy-2a(a-b) = 0 …………………………. (iv)
By cross multiplication
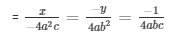
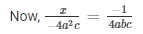
= x = a/b
And,
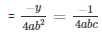
= y = b/c
The solution of the system of equations are a/b and b/c
Q20
(a-b)x + (a + b)y = 2a2-2b2
(a + b)(x + y) = 4ab
Soln.
The given system of equations are :
(a-b)x + (a + b)y = 2a2-2b2 ………………………….. (i)
(a + b)(x + y) = 4ab …………………………. (ii)
From equation (i)
(a-b)x + (a + b)y-2a2-2b2 = 0
= (a-b)x + (a + b)y-2(a2-b2) = 0
From equation (ii)
(a-b)x + (a-b)y-4ab = 0
Here, a1 = a-b , b1 = a + b , c1 = -2(a2 + b2)
Here, a2 = a + b , b2 = a + b , c2 = -4ab
By cross multiplication method
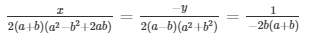
Now,
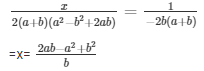
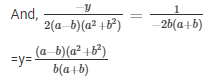
The solution of the system of equations are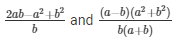 respectively.
respectively.
Q21
a2x + b2y = c2
b2x + a2y = d2
Sol.
The given system of equations are :
a2x + b2y = c2 ………………………………….. (i)
b2x + a2y = d2……………………………………… (ii)
Here, a1 = a2 , b1 = b2 , c1 = -c2
Here, a2 = b2 , b2 = a2 , c2 = -d2
By cross multiplication method
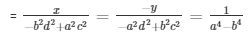
Now,
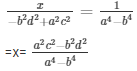
And = 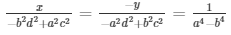
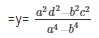
The solution of the given system of equations are 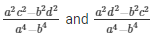 respectively.
respectively.
Q23
2(ax-by + a + 4b = 0
2(bx + ay) + b-4a = 0
Sol. The given system of equation may be written as :
2(ax-by + a + 4b = 0 …………………….. (i)
2(bx + ay) + b-4a = 0……………………. (ii)
Here, a1 = 2a , b1 = -2b , c1 = a + 4b
Here, a2 = 2b , b2 = 2a , c2 = b-4a
By cross multiplication method
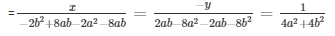
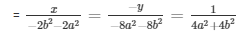
Now, 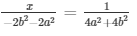
= x = -1/2
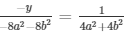
x − 2b2 − 2a2 = 14a2 + 4b2
= x = − 12
And, − y − 8a2 − 8b2 = 14a2 + 4b2
= y = 2
The solution of the given pair of equations are − 1/2 and 2 respectively.
Q24
6(ax + by) = 3a + 2b
6(bx-ay) = 3b-2a
Sol. The systems of equations are
6(ax + by) = 3a + 2b ………………………… (i)
6(bx-ay) = 3b-2a …………………………. (ii)
From equation (i)
6ax + 6by-(3a + 2b) = 0 ……………………… (iii)
From equation (ii)
6bx-6ay-(3b-2a) = 0 …………………………… (iv)
Here, a1 = 6a , b1 = 6b , c1 = -(3a + 2b)
Here, a2 = 6b , b2 = -6a , c2 = -(3b-2a)
By cross multiplication method
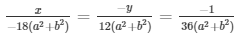
Now, 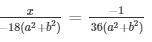
= x = 1/2
And , 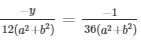
= y = 1/3
The solution of the given pair of equations are 1/2 and 1/3 respectively.
Q25
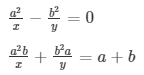
Sol. The given systems of equations are
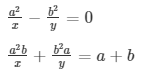
Taking 1/x = u
Taking 1/y = v
The pair of equations becomes:
a2u-b2v = 0
a2bu + b2av-(a + b) = 0
Here, a1 = a2 , b1 = -b2 , c1 = 0
Here, a2 = a2b , b2 = b2a , c2 = -(a + b)
By cross multiplication method
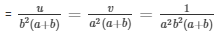
Now, 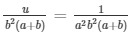
= x = 1/a2
And, 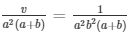
= y = 1/b2
The solution of the given pair of equations are 1/a2 and 1/b2 respectively.
Q26
mx-my = m2 + n2
x + y = 2m
Sol. mx-my = m2 + n2………………………………… (i)
x + y = 2m…………………………………………….. (ii)
Here, a1 = m , b1 = -n , c1 = -(m2 + n2)
Here, a2 = 1 , b2 = 1 , c2 = -(2m)
By cross multiplication method
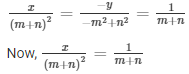
= x = m + n
And, 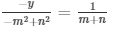
= y = m-n
The solutions of the given pair of equations are m + n and m-n respectively.
Q27
ax/b − by/a = a + b
ax-by = 2ab
Sol. The given pair of equations are:
ax/b − by/a = a + b ……………………….. (i)
ax-by = 2ab …………………………….. (ii)
Here, a1 = a/b , b1 = – b/a , c1 = -(a + b)
Here, a2 = a , b2 = – b, c2 = -(2ab)
By cross multiplication method
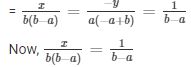
= x = b
And , 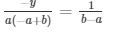
= y = -a
The solution of the given pair of equations are b and –a respectively.
Q28
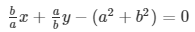
X + y-2ab = 0
Sol.
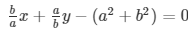 ………………….. (i)
………………….. (i)
X + y-2ab = 0…………………………………………. (ii)
Here, a1 = b/a , b1 = a/b , c1 = -(a2 + b2)
Here, a2 = 1 , b2 = -1, c2 = -(2ab)
By cross multiplication method
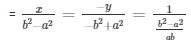
Now, 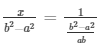
= x = ab
And, 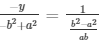
= y = ab
The solutions of the given pair of equations are ab and ab respectively.
|
5 videos|292 docs|59 tests
|
FAQs on Ex-3.4 Pair Of Linear Equations In Two Variables, Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. What are linear equations in two variables? |  |
| 2. How do you solve a pair of linear equations in two variables? |  |
| 3. Can a pair of linear equations have more than one solution? |  |
| 4. How do you determine if a pair of linear equations is consistent or inconsistent? |  |
| 5. Can a pair of linear equations have infinitely many solutions? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















