Ex-3.5 Pair Of Linear Equations In Two Variables (Part - 1), Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
In each of the following systems of equation determine whether the system has a unique solution, no solution or infinite solutions. In case there is a unique solution, find it from 1 to 4:
(1) x − 3y − 3 = 0
3x − 9y − 2 = 0
Sol.
The given system may be written as
x − 3y − 3 = 0
3x − 9y − 2 = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 1,b1 = − 3,c1 = − 3
a2 = 3,b2 = − 9,c2 = − 2
We have,
a1/a2 = 1/3
b1/b2 = − 3/ − 9 = 13
and , c1/c2 = − 3/ − 2 = 3/2
a1/a2 = b1/b2 ≠ c1/c2
Therefore, the given equation has no solution.
(2) 2x + y − 5 = 0
4x + 2y − 10 = 0
Sol.
The given system may be written as
2x + y − 5 = 0
4x + 2y − 10 = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 2,b1 = 1,c1 = − 5
a2 = 4,b2 = 2,c2 = − 10
We have,
a1/a2 = 2/4 = 1/2
b1/b2 = 1/2
and , c1/c2 = − 5/ − 10 = 1/2
So, a1/a2 = b1/b2 = c1/c2
Therefore, the given equation has infinitely many solution.
(3) 3x − 5y = 20
6x − 10y = 40
Sol.
The given system may be written as
3x − 5y = 20
6x − 10y = 40
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 3,b1 = − 5,c1 = − 20
a2 = 6,b2 = − 10,c2 = − 40
We have,
a1/a2 = 3/6 = 1/2
b1/b2 = − 5/ − 10 = 1/2
and , c1/c2 = − 20 /− 40 = 1/2
So, a1/a2 = b1/b2 = c1/c2
Therefore, the given equation has infinitely many solution.
(4) x − 2y − 8 = 0
5x − 10y − 10 = 0
Sol.
The given system may be written as
x − 2y − 8 = 0
5x − 10y − 10 = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 1,b1 = − 2,c1 = − 8
a2 = 5,b2 = − 10,c2 = − 10
We have,
a1/a2 = 1/5
b1/b2 = − 2 /− 10 = 1/5
and , c1/c2 = − 8/ − 10 = 4/5
a1/a2 = b1/b2 ≠ c1/c2
Therefore, the given equation has no solution.
Find the value of k for each of the following system of equations which have a unique solution (5-8)
(5) kx + 2y − 5 = 0
3x + y − 1 = 0
Sol.
The given system may be written as
kx + 2y − 5 = 0
3x + y − 1 = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = k,b1 = 2,c1 = − 5
a2 = 3,b2 = 1,c2 = − 1
For unique solution,we have
a1/a2 ≠ b1/b2
k/3 ≠ 2/1
⇒ k ≠ 6
Therefore, the given system will have unique solution for all real values of k other than 6.
(6) 4x + ky + 8 = 0
2x + 2y + 2 = 0
Sol.
The given system may be written as
4x + ky + 8 = 0
2x + 2y + 2 = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 4,b1 = k,c1 = 8
a2 = 2,b2 = 2,c2 = 2
For unique solution,we have
a1/a2 ≠ b1/b2
4/2 ≠ k/2
⇒ k ≠ 4
Therefore, the given system will have unique solution for all real values of k other than 4.
(7) 4x − 5y = k
2x − 3y = 12
Sol.
The given system may be written as
4x − 5y − k = 0
2x − 3y − 12 = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 4,b1 = − 5,c1 = − k
a2 = 2,b2 = − 3,c2 = − 12
For unique solution,we have
a1a2 ≠ b1b2
4/2 ≠ − 5/ − 3
⇒ k can have any real values.
Therefore, the given system will have unique solution for all real values of k.
(8) x + 2y = 3
5x + ky + 7 = 0
Sol.
The given system may be written as
x + 2y = 3
5x + ky + 7 = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 1,b1 = 2,c1 = − 3
a2 = 5,b2 = k,c2 = 7
For unique solution,we have
a1a2 ≠ b1b2
1/5 ≠ 2/k
⇒ k ≠ 10
Therefore, the given system will have unique solution for all real values of k other than 10.
Find the value of k for which each of the following system of equations having infinitely many solution: (9-19)
(9) 2x + 3y − 5 = 0
6x − ky − 15 = 0
Sol.
The given system may be written as
2x + 3y − 5 = 0
6x − ky − 15 = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 2,b1 = 3,c1 = − 5
a2 = 6,b2 = k,c2 = − 15
For unique solution,we have
a1/a2 = b1/b2 = c1/c2
2/6 ≠ 3/k
⇒ k = 9
Therefore, the given system of equation will have infinitely many solutions, if k = 9.
(10) 4x + 5y = 3
kx + 15y = 9
Sol.
The given system may be written as
4x + 5y = 3
kx + 15y = 9
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 4,b1 = 5,c1 = 3
a2 = k,b2 = 15,c2 = 9
For unique solution,we have
a1/a2 = b1/b2 = c1/c2
4/k = 5/15 = − 3/ − 9
4/k = 1/3
⇒ k ≠ 12
Therefore, the given system will have infinitely many solutions if k = 12.
(11) kx − 2y + 6 = 0
4x + 3y + 9 = 0
Sol.
The given system may be written as
kx − 2y + 6 = 0
4x + 3y + 9 = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = k,b1 = − 2,c1 = 6
a2 = 4,b2 = − 3,c2 = 9
For unique solution,we have
a1/a2 = b1/b2 = c1/c2
k/4 = − 2 /− 3 = 2/3
⇒ k = 8/3
Therefore, the given system of equations will have infinitely many solutions, if k = 8/3.
(12) 8x + 5y = 9
kx + 10y = 19
Sol.
The given system may be written as
8x + 5y = 9
kx + 10y = 19
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 8,b1 = 5,c1 = − 9
a2 = k,b2 = 10,c2 = − 18
For unique solution,we have
a1/a2 = b1/b2 = c1/c2
8/k = 5/10 = − 9 /− 18 = 1/2
⇒ k = 16
Therefore, the given system of equations will have infinitely many solutions, if k = 16.
(13) 2x − 3y = 7
(k + 2)x − (2k + 1)y = 3(2k − 1)
Sol.
The given system may be written as
2x − 3y = 7
(k + 2)x − (2k + 1)y = 3(2k − 1)
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 2,b1 = − 3,c1 = − 7
a2 = k,b2 = − (2k + 1),c2 = − 3(2k − 1)
For unique solution,we have
a1/a2 = b1/b2 = c1/c2
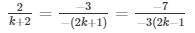
 and
and 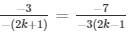
⇒ 2(2k + 1) = 3(k + 2) and 3×3(2k − 1) = 7(2k + 1)
⇒ 4k + 2 = 3k + 6 and 18k − 9 = 14k + 7
⇒ k = 4 and 4k = 16⇒ k = 4
Therefore, the given system of equations will have infinitely many solutions, if k = 4.
(14) 2x + 3y = 2
(k + 2)x + (2k + 1)y = 2(k − 1)
Sol.
The given system may be written as
2x + 3y = 2
(k + 2)x + (2k + 1)y = 2(k − 1)
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 2,b1 = 3,c1 = − 2
a2 = (k + 2),b2 = (2k + 1),c2 = − 2(k − 1)
For unique solution,we have
a1/a2 = b1/b2 = c1/c2
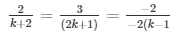
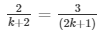 and
and 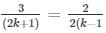
⇒ 2(2k + 1) = 3(k + 2) and 3(k − 1) = (2k + 1)
⇒ 4k + 2 = 3k + 6 and 3k − 3 = 2k + 1
⇒ k = 4 and k = 4
Therefore, the given system of equations will have infinitely many solutions, if k = 4.
(15) x + (k + 1)y = 4
(k + 1)x + 9y = (5k + 2)
Sol.
The given system may be written as
x + (k + 1)y = 4
(k + 1)x + 9y = (5k + 2)
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 1,b1 = (k + 1),c1 = − 4
a2 = (k + 1),b2 = 9,c2 = − (5k + 2)
For unique solution,we have
a1/a2 = b1/b2 = c1/c2
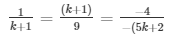
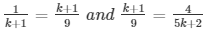
⇒ 9 = (k + 1)2 and (k + 1)(5k + 2) = 36
⇒ 9 = k2 + 2k + 1 and 5k2 + 2k + 5k + 2 = 36
⇒ k2 + 2k − 8 = 0 and 5k2 + 7k − 34 = 0
⇒ k2 + 4k − 2k − 8 = 0 and 5k2 + 17k − 10k − 34 = 0
⇒ k(k + 4) − 2(k + 4) = 0 and (5k + 17) − 2(5k + 17) = 0
⇒ (k + 4)(k − 2) = 0 and (5k + 17)(k − 2) = 0
⇒ k = − 4 ork = 2 and k = − 17/5 ork = 2
thus, k = 2 satisfies both the condition.
Therefore, the given system of equations will have infinitely many solutions, if k = 2.
(16) kx + 3y = 2k + 1
2(k + 1)x + 9y = (7k + 1)
Sol.
The given system may be written as
kx + 3y = 2k + 1
2(k + 1)x + 9y = (7k + 1)
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = k,b1 = 3,c1 = − (2k + 1)
a2 = 2(k + 1),b2 = 9,c2 = − (7k + 1)
For unique solution,we have
a1/a2 = b1/b2 = c1/c2
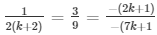
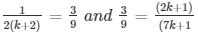
⇒ 9k = 3×2(k + 1) and 3(7k + 1) = 9(2k + 1)
⇒ 9k − 6k = 6 and 21k − 18k = 9 − 3
⇒ 3k = 6 and 3k = 6
⇒ k = 2 and k = 2
Therefore, the given system of equations will have infinitely many solutions, if k = 2.
(17) 2x + (k − 2)y = k
6x + (2k − 1)y = (2k + 5)
Sol.
The given system may be written as
2x + (k − 2)y = k
6x + (2k − 1)y = (2k + 5)
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 2,b1 = (k − 2),c1 = − k
a2 = 6,b2 = (2k − 1),c2 = − (2k + 5)
For unique solution,we have
a1/a2 = b1/b2 = c1/c2
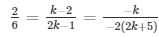
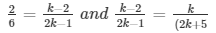
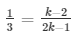 and 2k2 + 5k − 4k − 10 = 2k2 − k
and 2k2 + 5k − 4k − 10 = 2k2 − k
⇒ 2k − 3k = − 6 + 1 and k + k = 10
⇒ − k = − 5 and 2k = 10
⇒ k = 5 and k = 5
Therefore, the given system of equations will have infinitely many solutions, if k = 5.
(18) 2x + 3y = 7
(k + 1)x + (2k − 1)y = (4k + 1)
Sol.
The given system may be written as
2x + 3y = 7
(k + 1)x + (2k − 1)y = (4k + 1)
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 2,b1 = 3,c1 = − 7
a2 = k + 1,b2 = 2k − 1,c2 = − (4k + 1)
For unique solution,we have
a1/a2 = b1/b2 = c1/c2
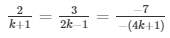
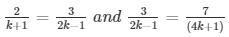
Extra close brace or missing open brace
⇒ 4k − 2 = 3k + 3 and 12k + 3 = 14k − 7
⇒ k = 5 and 2k = 10
⇒ k = 5 and k = 5
Therefore, the given system of equations will have infinitely many solutions, if k = 5.
(19) 2x + 3y = k
(k − 1)x + (k + 2)y = 3k
Sol.
The given system may be written as
2x + 3y = k
(k − 1)x + (k + 2)y = 3k
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 2,b1 = 3,c1 = − k
a2 = k − 1,b2 = k + 2,c2 = − 3k
For unique solution,we have
a1/a2 = b1/b2 = c1/c2
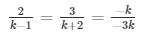
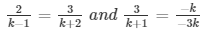
Extra close brace or missing open brace
⇒ 2k + 4 = 3k − 3 and 9 = k + 2
⇒ k = 7 and k = 7
Therefore, the given system of equations will have infinitely many solutions, if k = 7.
Find the value of k for which the following system of equation has no solution : (20-25)
(20) kx − 5y = 2
6x + 2y = 7
Sol.
The given system may be written as
kx − 5y = 2
6x + 2y = 7
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = k,b1 = − 5,c1 = − 2
a2 = 6,b2 = 2,c2 = − 7
For no solution,we have
a1/a2 = b1/b2 ≠ c1/c2
k/6 = − 5/2 ≠ 2/7
⇒ 2k = − 30
⇒ k = − 15
Therefore, the given system of equations will have no solutions, if k = − 15.
|
5 videos|292 docs|59 tests
|
FAQs on Ex-3.5 Pair Of Linear Equations In Two Variables (Part - 1), Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. How can I solve a pair of linear equations in two variables? |  |
| 2. What is the importance of solving linear equations in two variables? |  |
| 3. Can linear equations in two variables have more than one solution? |  |
| 4. What is the graphical representation of a pair of linear equations in two variables? |  |
| 5. How can I check if a given point is a solution to a pair of linear equations in two variables? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















