Ex-3.5 Pair Of Linear Equations In Two Variables (Part - 2), Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
(21) x + 2y = 0
2x + ky = 5
Sol.
The given system may be written as
x2y = 0
2x + ky = 5
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 1,b1 = 2,c1 = 0
a2 = 2,b2 = k,c2 = − 5
For no solution,we have
a1/a2 = b1/b2 ≠ c1/c2
1/2 = 2/k ≠ 2/7
⇒ k = 4
Therefore, the given system of equations will have no solutions, if k = 4.
(22) 3x − 4y + 7 = 0
kx + 3y − 5 = 0
Sol.
The given system may be written as
3x − 4y + 7 = 0
kx + 3y − 5 = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 3,b1 = − 4,c1 = 7
a2 = k,b2 = 3,c2 = − 5
For no solution,we have
a1/a2 = b1/b2 ≠ c1/c2
3/k = − 4/3
⇒ k = − 9/4
Therefore, the given system of equations will have no solutions, if k = − 9/4.
(23) 2x − ky + 3 = 0
3x + 2y − 1 = 0
Sol.
The given system may be written as
2x − ky + 3 = 0
3x + 2y − 1 = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 2,b1 = − k,c1 = 3
a2 = 3,b2 = 2,c2 = − 1
For no solution,we have
a1/a2 = b1/b2 ≠ c1/c2
2/3 = − k/2
⇒ k = − 4/3
Therefore, the given system of equations will have no solutions, if k = − 4/3.
(24) 2x + ky − 11 = 0
5x − 7y − 5 = 0
Sol.
The given system may be written as
2x + ky − 11 = 0
5x − 7y − 5 = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 2,b1 = k,c1 = − 11
a2 = 5,b2 = − 7,c2 = − 5
For no solution,we have
a1/a2 = b1/b2 ≠ c1/c2
2/5 = − k /− 7
⇒ k = − 14/5
Therefore, the given system of equations will have no solutions, if k = − 14/5.
(25) kx + 3y = 3
12x + ky = 6
Sol.
The given system may be written as
kx + 3y = 3
12x + ky = 6
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = k,b1 = 3,c1 = − 3
a2 = 12,b2 = k,c2 = − 6
For no solution,we have
a1/a2 = b1/b2 ≠ c1/c2
k/12 = 3/k ≠ 3/6 ……(i)
⇒ k2 = 36
⇒ k = + 6or − 6
From (i)
k/12 ≠ 3/6
⇒ k ≠ 6
Therefore, the given system of equations will have no solutions, if k = − 6.
(26) For what value of a, the following system of equation will be inconsistent?
4x + 6y − 11 = 0
2x + ay − 7 = 0
Sol.
The given system may be written as
4x + 6y − 11 = 0
2x + ay − 7 = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 4,b1 = 6,c1 = − 11
a2 = 2,b2 = a,c2 = − 7
For unique solution,we have
a1/a2 = b1/b2 ≠ c1/c2
a1/a2 = b1/b2
4/2 = 6/a
⇒ a = 3
Therefore, the given system of equations will be inconsistent, if a = 3.
(27) For what value of a, the following system of equation have no solution?
ax + 3y = a − 3
12x + ay = a
Sol.
The given system may be written as
ax + 3y = a − 3
12x + ay = a
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = a,b1 = 3,c1 = − (a − 3)
a2 = 12,b2 = a,c2 = − a
For unique solution,we have
a1/a2 = b1/b2 ≠ c1/c2
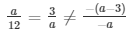
3/a ≠ frac − (a − 3) − a
⇒ a − 3 ≠ 3
⇒ a ≠ 6
and ,
a/12 = 3/a
⇒ a2 = 36
⇒ a = + 6or − 6
∵ a ≠ 6
⇒ a = − 6
Therefore, the given system of equations will have no solution, if a = − 6.
(28) Find the value of a,for which the following system of equation have
(i) Unique solution
(ii) No solution
kx + 2y = 5
3x + y = 1
Sol.
The given system may be written as
kx + 2y − 5 = 0
3x + y − 1 = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = k,b1 = 2,c1 = − 5
a2 = 3,b2 = 1,c2 = − 1
(i) For unique solution, we have
a1/a2 ≠ b1/b2
k/3 ≠ 2/1
k ≠ 6
Therefore, the given system of equations will have unique solution, if k ≠ 6.
(ii) For no solution, we have
a1/a2 = b1/b2 ≠ c1/c2
k/3 = 2/1 ≠ − 5/ − 1
k/3 = 2/1
⇒ k = 6
Therefore, the given system of equations will have no solution, if a = 6.
(29) For what value of c, the following system of equation have infinitely many solution (where c ≠ 0 )?
6x + 3y = c − 3
12x + cy = c
Sol.
The given system may be written as
6x + 3y − (c − 3) = 0
12x + cy − c = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 6,b1 = 3,c1 = − (c − 3)
a2 = 12,b2 = c,c2 = − c
For infinitely many solution,we have
a1/a2 = b1/b2 = c1/c2
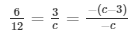
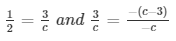
⇒ c = 6 and c − 3 = 3
⇒ c = 6 and c = 6
Therefore, the given system of equations will have infinitely many solution, if c = 6.
(30) Find the value of k,for which the following system of equation have
(i) Unique solution
(ii) No solution
(iii) Infinitely many solution
2x + ky = 1
3x − 5y = 7
Sol.
The given system may be written as
2x + ky = 1
3x − 5y = 7
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 2,b1 = k,c1 = − 1
a2 = 3,b2 = − 5,c2 = − 7
(i) For unique solution, we have
a1/a2 ≠ b1/b2
2/3 ≠ − k /− 5
k ≠ − 10/3
Therefore, the given system of equations will have unique solution, if k ≠ − 10/3.
(ii) For no solution, we have
a1/a2 = b1/b2 ≠ c1/c2
2/3 = k/ − 5 neq − 1/ − 7
2/3 = k/ − 5 and k /− 5 neq1 7
⇒ k = − 10/3 and k neq − 5/7
⇒ k = − 10/3
Therefore, the given system of equations will have no solution, if k = − 10/3.
(iii) For the given system to have infinitely many solution,we have
a1/a2 = b1/b2 = c1/c2
2/3 = k/ − 5 = − 1/ − 7
Clearly a1a2 ≠ c1c2 ,
So there is no value of k for which the given system of equation has infinitely many solution.
(31) For what value of k, the following system of equation will represent the coincident lines?
x + 2y + 7 = 0
2x + ky + 14 = 0
Sol.
The given system may be written as
x + 2y + 7 = 0
2x + ky + 14 = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 1,b1 = 2,c1 = 7
a2 = 2,b2 = k,c2 = 14
The given system of equation will represent the coincident lines if they have infinitely many solution.
a1/a2 = b1/b2 = c1/c2
1/2 = 2/k = 7/14
1/2 = 2/k = 1/2
⇒ k = 4
Therefore, the given system of equations will have infinitely many solution, if k = 4.
(32) (30) Find the value of k,for which the following system of equation have unique solution.
ax + by = c
lx + my = n
Sol.
The given system may be written as
ax + by − c = 0
lx + my − n = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = a,b1 = b,c1 = − c
a2 = l,b2 = m,c2 = − n
For unique solution, we have
a1/a2 ≠ b1/b2
⇒ a/l ≠ b/m
⇒ a/m ≠ b/l
Therefore, the given system of equations will have unique solution, if a/m ≠ b/l.
(33) Find the value of a and b such that the following system of linear equation have infinitely many solution:
(2a − 1)x + 3y − 5 = 0
3x + (b − 1)y − 2 = 0
Sol.
The given system of equation may be written as,
(2a − 1)x + 3y − 5 = 0
3x + (b − 1)y − 2 = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = (2a − 1),b1 = 3,c1 = − 5
a2 = 3,b2 = b − 1,c2 = − 2
The given system of equation will have infinitely many solution, if
a1/a2 = b1/b2 = c1/c2
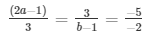
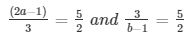
⇒ 2(2a − 1) = 15 and 6 = 5(b − 1)
⇒ 4a − 2 = 15 and 6 = 5b − 5
⇒ 4a = 17 and 5b = 11
⇒ a = 17/4 and b = 11/5
(34) Find the value of a and b such that the following system of linear equation have infinitely many solution:
2x − 3y = 7
(a + b)x − (a + b − 3)y = 4a + b
Sol.
The given system of equation may be written as,
2x − 3y − 7 = 0
(a + b)x − (a + b − 3)y − (4a + b) = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 2,b1 = − 3,c1 = − 7
a2 = (a + b),b2 = − (a + b − 3),c2 = − (4a + b)
The given system of equation will have infinitely many solution, if
a1/a2 = b1/b2 = c1/c2
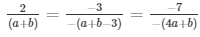
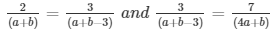
⇒ 2(a + b − 3) = 3(a + b) and 3(4a + b) = 7(a + b − 3)
⇒ 2a + 2b − 6 = 3a + 3b and 12a + 3b = 7a + 7b − 21
⇒ a + b = − 6 and 5a − 4b = − 21
a + b = -6
⇒ a = − 6 − b
Substituting the value of a in 5a − 4b = − 21 we have
5(-b-6)-4b = -21
⇒ − 5b − 30 − 4b = − 21
⇒ 9b = − 9
⇒ b = − 1
As a = -6-b
⇒ a = − 6 + 1 = − 5
Hence the given system of equation will have infinitely many solution if
a = -5 and b = -1.
(35) Find the value of p and q such that the following system of linear equation have infinitely many solution:
2x − 3y = 9
(p + q)x + (2p − q)y = 3(p + q + 1)
Sol.
The given system of equation may be written as,
2x − 3y − 9 = 0
(p + q)x + (2p − q)y − 3(p + q + 1) = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 2,b1 = 3,c1 = − 9
a2 = (p + q),b2 = (2p − q),c2 = − 3(p + q + 1)
The given system of equation will have infinitely many solution, if
a1/a2 = b1/b2 = c1/c2
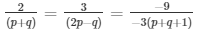
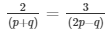 and
and 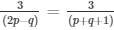
2(2p − q) = 3(p + q) and (p + q + 1) = 2p − q
⇒ 4p − 2q = 3p + 3q and − p + 2q = − 1
⇒ p = 5q and p − 2q = 1
Substituting the value of p in p-2q = 1, we have
3q = 1
⇒ q = 1/3
Substituting the value of p in p = 5q we have
p = 5/3
Hence the given system of equation will have infinitely many solution if
p = 5/3 and q = 1/3.
(36) Find the values of a and b for which the following system of equation has infinitely many solution:
(i) (2a − 1)x + 3y = 5
3x + (b − 2)y = 3
Sol.
The given system of equation may be written as,
(2a − 1)x + 3y − 5 = 0
3x + (b − 2)y − 3 = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 2a − 1,b1 = 3,c1 = − 5
a2 = 3,b2 = b − 2,c2 = − 3(p + q + 1)
The given system of equation will have infinitely many solution, if
a1/a2 = b1/b2 = c1/c2
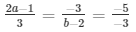
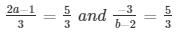
2a − 1 = 5 and − 9 = 5(b − 2)
⇒ a = 3 and − 9 = 5b − 10
⇒ a = 3 and b = 1/5
Hence the given system of equation will have infinitely many solution if
a = 3 and b = 1/5.
(ii) 2x − (2a + 5)y = 5
(2b + 1)x − 9y = 15
Sol.
The given system of equation may be written as,
2x − (2a + 5)y = 5
(2b + 1)x − 9y = 15
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 2,b1 = − (2a + 5),c1 = − 5
a2 = (2b + 1),b2 = − 9,c2 = − 15
The given system of equation will have infinitely many solution, if
a1/a2 = b1/b2 = c1/c2
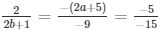
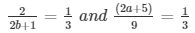
⇒ 6 = 2b + 1 and 2a + 5 = 3
⇒ b = 5/2 and a = − 1
Hence the given system of equation will have infinitely many solution if
a = − 1 and b = 5/2.
(iii) (a − 1)x + 3y = 2
6x + (1 − 2b)y = 6
Sol.
The given system of equation may be written as,
(a − 1)x + 3y = 2
6x + (1 − 2b)y = 6
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = a − 1,b1 = 3,c1 = − 2
a2 = 6,b2 = 1 − 2b,c2 = − 6
The given system of equation will have infinitely many solution, if
a1/a2 = b1/b2 = c1/c2
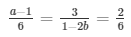
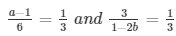
⇒ a − 1 = 2 and 1 − 2b = 9
⇒ a = 3 and b = − 4
Hence the given system of equation will have infinitely many solution if
a = 3 and b = − 4.
(iv) 3x + 4y = 12
(a + b)x + 2(a − b)y = 5a − 1
Sol.
The given system of equation may be written as,
3x + 4y − 12 = 0
(a + b)x + 2(a − b)y − (5a − 1) = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 3,b1 = 4,c1 = − 12
a2 = (a + b),b2 = 2(a − b),c2 = − (5a − 1)
The given system of equation will have infinitely many solution, if
a1/a2 = b1/b2 = c1/c2
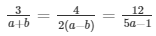
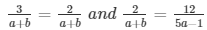
⇒ 3(a − b) = 2a + 2b and 2(5a − 1) = 12(a − b)
⇒ a = 5b and − 2a = − 12b + 2
Substituting a = 5b in -2a = -12b + 2 , we have
-2(5b) = -12b + 2
⇒ − 10b = − 12b + 2
⇒ b = 1
Thus a = 5
Hence the given system of equation will have infinitely many solution if
a = 5 and b = 1.
(v) 2x + 3y = 7
(a − 1)x + (a + 1)y = 3a − 1
Sol.
The given system of equation may be written as,
2x + 3y − 7 = 0
(a − 1)x + (a + 1)y − (3a − 1) = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 2,b1 = 3,c1 = − 7
a2 = (a − 1),b2 = (a + 1),c2 = − (3a − 1)
The given system of equation will have infinitely many solution, if
a1/a2 = b1/b2 = c1/c2
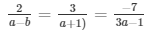
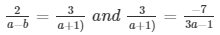
⇒ 2(a + 1) = 3(a − 1) and 3(3a − 1) = 7(a + 1)
⇒ 2a − 3a = − 3 − 2 and 9a − 3 = 7a + 7
⇒ a = 5 and a = 5
Hence the given system of equation will have infinitely many solution if
a = 5 and b = 1.
(vi) 2x + 3y = 7
(a − 1)x + (a + 2)y = 3a
Sol.
The given system of equation may be written as,
2x + 3y − 7 = 0
(a − 1)x + (a + 2)y − 3a = 0
The given system of equation is of the form
a1x + b1y − c1 = 0
a2x + b2y − c2 = 0
Where, a1 = 2,b1 = 3,c1 = − 7
a2 = (a − 1),b2 = (a + 2),c2 = − 3a
The given system of equation will have infinitely many solution, if
a1/a2 = b1/b2 = c1/c2
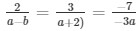
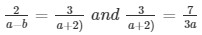
⇒ 2(a + 2) = 3(a − 1) and 3(3a) = 7(a + 2)
⇒ 2a + 4 = 3a − 3 and 9a = 7a + 14
⇒ a = 7 and a = 7
Hence the given system of equation will have infinitely many solution if
a = 7 and b = 1..
|
5 videos|292 docs|59 tests
|
FAQs on Ex-3.5 Pair Of Linear Equations In Two Variables (Part - 2), Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. What are linear equations in two variables? |  |
| 2. How can we solve a pair of linear equations in two variables? |  |
| 3. What is the importance of solving linear equations in two variables? |  |
| 4. Can a pair of linear equations in two variables have no solution? |  |
| 5. How can we verify the solution of a pair of linear equations in two variables? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|

















