Ex-4.4 Triangles, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Q1) In fig. (i) if AB∥CD, find the value of x.
Sol: (i) it is given that AB∥CD
We have to find the value of x.
Diagonals of the parallelogram,
As we know, DO/OA = CO/OB
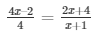
4(2x + 4) = (4x – 2)(x +1)
8x + 16 = x(4x – 2) + 1(4x – 2)
8x + 16 = 4x2 – 2x + 4x – 2
-4x2 + 8x + 16 + 2 – 2x = 0
-4x2 + 6x + 8 = 0
4x2 – 6x – 18 = 0
4x2 – 12x + 6x – 18 = 0
4x(x – 3) + 6(x – 3) = 0
(4x + 6) (x – 3) = 0
X = – 6/4 or x = 3
(ii) In fig. if AB∥CD, find the value of x.
Sol: (ii) it is given that AB∥CD
We need to find the value of x.
Now, DO/OA = CO/OB
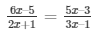
(6x – 5)(3x – 1) = (2x + 1)(5x – 3)
3x(6x – 5) – 1(6x – 5) = 2x(5x – 3) + 1(5x – 3)
18x2 – 10x2 – 21x + 5 + x +3 = 0
8x2 – 16x – 4x + 8 = 0
8x(x – 2) – 4(x – 2) = 0
(8x – 4)(x – 2) = 0
X = 4/8 = 1/2 or x = -2
X = 1/2
(iii) in fig. if AB∥CD .and OA = 3x – 19, OB = x – 4, OC = x- 3 and OD = 4, find x.
Sol: (iii) it is given that AB∥CD
And OA = 3x – 19 OB = x – 4 OC = x – 3 and OD = 4
We need to find the value of x,
Now, Now, AO/OC = BO/OD
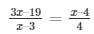
4(3x – 19) = (x – 3) (x – 4)
12x – 76 = x(x – 4) -3(x – 4)
12x – 76 = x2 – 4x – 3x + 12
-x2 + 7x – 12 + 12x -76 = 0
-x2 + 19x – 88 = 0
X2 – 19x + 88 = 0
X2 – 11x – 8x + 88 = 0
X(x – 11) – 8(x – 11) = 0
X = 11 or x = 8
|
5 videos|292 docs|59 tests
|
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















