Ex-4.7 Triangles, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
1 If the sides of a triangle are 3 cm, 4 cm, and 6 cm long, determine whether the hiangle is a right-angled triangle.
Sol:
We have,
Sides of triangle AB= 3 cm
BC= 4 cm
AC= 6 cm
∴ AB2 = 32 = 9
BC2 = 42 = 16
AC2 = 62 = 36
Since, AB2 + BC2 ≠ AC2
Then, by converse of Pythagoras theorem, triangle is not a right Mangle.
2. The sides of certain triangles are given below. Determine which of them right triangles are.
(i) a = 7 cm, b = 24 cm and c = 25 cm
(ii) a = 9 cm, b =16 cm and c = 18 cm
(iii) a = 1.6 cm, b= 3.8 cm and c = 4 cm
(iv) a = 8 cm, b = 10 cm and c = 6 cm
Sol: We have,
a= 7 cm, b = 24 cm and c = 25 cm
∴ a2 = 49, b2= 576 and c2 = 625
Since, a2 + b2 = 49 + 576
= 625
= c2
Then, by converse of Pythagoras theorem, given triangle is a right triangle.
We have,
a= 9 cm, b = 16 cm and c = 18 cm
∴ a2 = 81,b2= 256 and c2 = 324
Since, a2 + b2 = 81 + 256 = 337 ≠ c2
Then, by converse of Pythagoras theorem, given triangle is not a light triangle.
We have,
a=1.6 cm,b= 3.8 cmandC= 4 cm
∴ a2 = 64, b2 = 100 and c2 = 36
Since, a2 + c2 = 64 + 36 = 100 = b2
Then, by converse of Pythagoras theorem, given Mangle is a right triangle.
3. A man goes 15 metres due west and then 8 metres due north. How far is he from the starting point?
Sol:
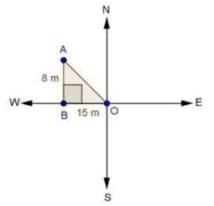
Let the starting point of the man be 0 and final point be A.
∴ In ΔABO, by Pythagoras theorem AO2 = AB2 + B02
⇒ AO2 = 82 + 152
⇒ AO2 = 64 + 225 = 289
⇒ AO =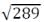 = 17m
= 17m
∴ He is 17m far from the starting point.
4. A ladder 17 m long reaches a window of a building 15 m above the ground. Find the distance of the foot of the ladder from the building.
Sol:
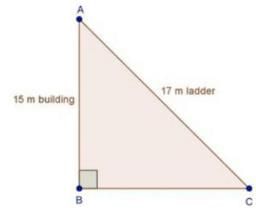
In ΔABC, by Pythagoras theorem AB2 + BC2 = AC2
⇒ 152 + BC2 = 172
⇒ 225 + BC2 = 172
= BC3 = 289 — 225
⇒ BC2 = 64
⇒ BC = 8
∴ Distance of the foot of the ladder from building = 8m
5. Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops.
Sol:
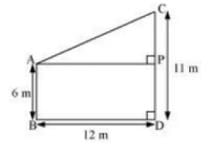
Let CD and AB be the poles of height 11 and 6 m. Therefore CP = 11 — 6 = 5 m
From the figure we may observe that AP = 12m In triangle APC, by applying Pythagoras theorem AP2 + PC2 AC2
122+ 52 = AC2
AC2 = 144 + 25 = 169
AC = 13
Therefore distance between their tops = 13m.
6. In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
Sol:
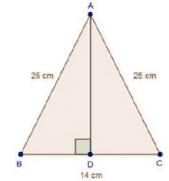
We have
AB = AC = 25 cm and BC = 14 cm
In ΔABD and ΔACD
∠ADB = ∠ADC [Each 90°]
AB = AC [Each 25 cm]
AD = AD [Common]
Then, ΔABD ≌ ΔACD [By RHS condition]
, BD = CD = 7 cm [By c.p.c.t]
In AADB, by Pythagoras theorem
AD2 + BD2 = AB2
⇒ AD2 + 72 = 252
⇒ AD2 = 625 — 49 = 576
⇒ AD = 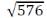 = 24 cm
= 24 cm
7. The foot of a ladder is 6 m away from a wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its tip reach?
Sol:
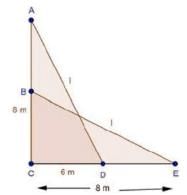
Let, length of ladder be AD = BE = I m In ΔACD, by Pythagoras theorem
AD2 = AC2 + CD2
l2 = 82 + 62 .............(ii)
In ΔBCE, by pythagoras theorem BE2 = BC2 + CE2
⇒ l2 = BC2 + 82 .............(ii)
Compare (i)and (ii) BC2 + 82 = 82 + 62
⇒ BC2 = 62
⇒ BC = 6m
8. Two poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops.
Sol:
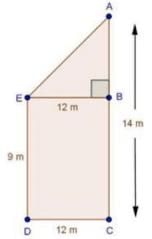
We have,
AC= 14m, DC= 12m and ED = BC = 9m
Construction: Draw EB ⊥ AC
∴ AB = AC — BC = 14 — 9 = 5m
And, EB = DC = 12m
In ΔABE, by Pythagoras theorem,
AE2 = AB2 + BE2
⇒ AE2 = 52 +122
⇒ AE2 = 25 + 144 =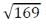
⇒ AE= VW) = 13m
∴ Distance between their tops = 13 m
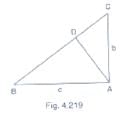
9. Using Pythagoras theorem determine the length of AD in terms of b and c shown in Fig. 4.219
Sol:
We have,
In ABAC, by Pythagoras theorem BC2 = An2 + AC2
⇒ BC2 = c2 + b2
⇒ BC = 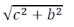
In ΔABD and MBA
∠B = ∠B [Common]
∠ADB = ∠BAC [Each 90°]
Then, ΔABD ∼ ΔCBA [By AA similarity]
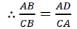 [Corresponding parts of similar A are proportional]
[Corresponding parts of similar A are proportional]
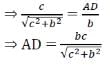
10. A triangle has sides 5 cm, 12 cm and 13 cm. Find the length to one decimal place, of the perpendicular from the opposite vertex to the side whose length is 13 cm.
Sol:

Let, AB = 5cm, BC = 12 cm and AC = 13 cm. Then, AO2 = AB2 + BC2 . This proves that ΔABC is a right triangle, right angles at B. Let BD be the length of perpendicular from B on AC.
Now, Area ΔABC = 1/2(BC X BA)
= 1/2 (12 X 5)
= 30 cm2
Also, Area of ΔABC = 1/2 AC X BD = 1/2 (13 X BD)
⇒ (13 XBD) = 30 X 2
⇒ BD = 60/13 cm
|
5 videos|292 docs|59 tests
|
FAQs on Ex-4.7 Triangles, Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. How can I find the area of a triangle using the RD Sharma Solutions for Class 10 Maths? |  |
| 2. What is the Pythagorean theorem and how is it used to solve triangle problems in RD Sharma Solutions for Class 10 Maths? |  |
| 3. How do I determine the types of triangles using RD Sharma Solutions for Class 10 Maths? |  |
| 4. How can I find the length of one side of a triangle using the RD Sharma Solutions for Class 10 Maths? |  |
| 5. How do I determine the congruence of two triangles using RD Sharma Solutions for Class 10 Maths? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















