All Courses
Get the App Signup / Login
Sign in Open App
Class 10 Exam  >  Class 10 Notes  >  Extra Documents, Videos & Tests for Class 10  >  RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths

Ex-7.3 Statistics, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download

1. The following table gives the distribution of total household expenditure (in rupees) of manual workers in a city.

Expenditure (in rupees) (x)Frequency (fi)Expenditure (in rupees) (xi)Frequency (fi)
100 – 150 24300 – 35030
150 – 200 40350 – 40022
200 – 25033400 – 45016
250 – 30028450 – 5007

Find the average expenditure (in rupees) per household

Sol: Let the assumed mean (A) = 275

Class intervalMid value (xi)di = xi – 275ui = (xi-275)/50Frequency fifiui
100 – 150125-150-324-12
150 – 200175-100-240-80
200 – 250225-50-133-33
250 – 30027500280
300 – 3503255013030
350 – 40037510022244
400 – 45042515031648
450 – 5004752004728
    N = 200Sum = -35

We have

A = 275, h = 50

Mean = A + h * sum/N = 275 + 50 * -35/200 = 275 – 8.75 = 266.25

 

2. A survey was conducted by a group of students as a part of their environmental awareness program, in which they collected the following data regarding the number of plants in 200 houses in a locality. Find the mean number of plants per house.

Number of plants:0-2          2-4          4-6          6-B         8-10       10-12     12-14
Number of houses:1              2              1              5              6              2              3

Which method did you use for finding the mean, and why?

Sol:

Let us find class marks (xi­) = (upper class limit + lower class limit)/2

Now we may compute xi and fixi as following.

 

Number of plantsNumber of house (fi)xiFixi
0 – 2111
2 – 4236
4 – 6155
6 – 85735
8 – 106954
10 – 1221122
12 – 1431339
TotalN = 20 Sum = 162

From the table we may observe that

N = 20

Sum = 162

Mean 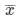 Ex-7.3 Statistics, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 = Sum/N

162/20 = 8.1

So mean number of plants per house is 8.1

We have used for the direct method values Xi and fi are very small

 

3. Consider the following distribution of daily wages of workers of a factory

Daily wages (in Rs)100-120                120-140                140-160                160-180                180-200
Number of workers:12                           16                           8                              6                              10

Find the mean daily wages of the workers of the factory by using an appropriate method.

Sol: Let the assume mean (A) = 150

Class intervalMid value xidi = xi – 150ui = (xi-150)/20Frequency fiFiui
100 – 120110-40-212-24
120 – 140130-20-114-14
140 – 1601500080
160 – 18017020166
180 – 2001904021020
   N = 50Sum = -12 

We have

N = 50, h = 20

Mean = A + h x sum/N

= 150 + 2 x (-15)/5

= 150 – 4.8

= 145.2

 

4.Thirty women were examined in a hospital by a doctor and the number of heart beats per minute recorded and summarized as follows. Find the mean heart beats per minute for these women, choosing a suitable method.

Number of heart

Beats Per minute:65 – 68   68 – 71   71 – 74   74 – 77   77 – 80   80 – 83   83 – 86
Number of women:2                   4              3              8              7              4              2

Sol: we may find marks of each interval (xi) by using the relation

(xi­) = (upper class limit + lower class limit)/2

Class size of this data = 3

Now talking 75.5 as assumed mean (a)

We may calculate di, ui, fiui as following

Number of heart beats per minuteNumber of women (xi)xidi = xi – 75.5ui = (xi – 755)/hfiui
65-68266.5-9-3-6
68-71969.5-6-2-8
71-74372.5-3-1-3
74-77875.5000
77-80778.5317
80-83481.5628
83-86284.5936
 N = 30   Sum = 4

Now we may observe from table that N = 30, sum = 4

Mean 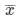Ex-7.3 Statistics, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10= 75.5 + (4/3)x3

= 75.5 + 0.4

= 75.9

So mean heart beats per minute for those women are 75.9 beats per minute

 

5.Find the mean of each of the following frequency distributions: (5 – 14)

Class interval:  0-6          6-12       12-18     18-24     24-30
Frequency:        6              8              10           9              7

Sol:

Let us assume mean be 15

Class intervalMid – valuedi = xi – 15ui = (xi – 15)/6fifiui
0 – 63-12-26-12
6 – 129-6-18-8
12 – 181500100
18 – 24216199
24 – 3027182714
    N = 40Sum = 3

A = 15, h = 6

Mean = A + h(sum/A)

= 15 + 6(3/40)

= 15 + 0.45

= 15.45

 

6.

Class interval:50-70     70-90     90-110   110-130     130-150      150-170
Frequency:18              12           13             27                      8              22

Sol: Let us assumed mean be 100

Class intervalMid-value xidi = xi – 100ui = (xi – 100)/20fifiui
50 – 7060-40-218-36
70 – 9080-20-112-12
90 – 11010000130
110 – 1301202012727
130 – 150140402816
150 – 1701606032266
     61

A = 100, h = 20

Mean    = 100 + 20 (61/100)

= 100 + 12.2

= 112.2

 

7.

Class interval:0-8          8-16       16-24     24-32     32-40
Frequency:6              7              10           8              9

Sol: Let the assumed mean (A) = 20

Class intervalMid- valuedi= xi – 20ui = (xi – 20)/8fifiui
0-84-16-26-12
8-1612-8-17-7
16-242000100
24-32288188
32-4036162918
    N = 40Sum = 7

We have A = 20, h = 8

Mean= A + h (sum/N)

= 20 + 8 (7/40)

= 20 + 1.4

= 21.4

 

8.

Class interval:0 – 6                       6 – 12                    12 – 18                  18 – 24                  24 – 30
Frequency:7                              5                              10                           12                           6

Sol: Let the assumed mean be (A) = 15

Class intervalMid – valuedi = xi -15ui = (xi -15)/6Frequency fifiui
0 – 63-12-2-1-14
6 – 129-6-15-5
12 – 181500100
18 – 2421611212
24 – 3027122612
    N = 40Sum = 5

We have

A = 15, h = 6

Mean = A + h(sum/N)

= 15 + 6 (5/40)

= 15 + 0.75

= 15.75

 

9.

Class interval:0 – 10                    10 – 20                  20 – 30                  30 – 40                  40 – 50
Frequency:9                              12                           15                           10                           14

Sol: Let the assumed mean (A) = 25

Class intervalMid – valuedi = xi -25ui = (xi -25)/10Frequency fifiui
0 – 105-20-29-18
10 – 2015-10-110-12
20 – 302500150
30 – 40351011010
40 – 50452021428
    N = 60Sum = 8

We have A = 25, h = 10

Mean    = A + h(sum/N)

= 25 + 19 (8/60)

= 25 + (4/3)

= 26.333


10.

Class interval:0-8          8-16       16-24     24-32     32-40
Frequency:5              9              10           8              8

Sol: Let the assumed mean (A) = 20

Class intervalMid value xidi= xi – 20ui = (xi -20)/8Frequency fifiui
0-84-16-25-10
8-1612-8-19-9
16-242000100
24-32288188
32-4036162816
    N = 40Sum = 5

We have,

A = 20, h = 8

Mean    = A + h (sum/N)

= 20 + 8 (5/ 40)

= 20 + 1

= 21

 

11.

Class interval:0-8          8-16       16-24     24-32     32-40
Frequency:5              6              4              3              2

Sol: Let the assumed mean (A) = 20

Class intervalMid value xidi= xi – 20ui = (xi -20)/8Frequency fifiui
0-84-16-2-2-10
8-1612-8-1-1-6
16-24200000
24-32288113
32-403616224
    N = 20Sum = -9

We have,

A = 20, h = 8

Mean = A + h (sum/N)

= 20 + 8 (-9/ 20)

= 20 – (72/20)

= 20 – 3.6

= 16.4

 

12.

Class interval:10-30     30-50     50-70     70-90     90-110   110-130
Frequency:5              8              12           20           3              2

Sol: Let the assumed mean (A) = 60

Class intervalMid value xidi= xi – 60ui = (xi -60)/20Frequency fifiui
10 – 3020-40-25-10
30 – 5040-20-18-8
50 – 706000120
70 – 90802012020
90 – 11010040236
110 – 13012060326
    N = 50Sum = 14

We have

A = 60, h = 20

Mean = A + h (sum/N)

= 60 + 20 (14/ 5)

= 60 + 5.6

= 65.6

 

13.

Class interval:25-35     35-45     45-55     55-65     65-75
Frequency:6              10           8              10           4

Sol: Let the assumed mean (A) = 50

Class intervalMid value xidi= xi – 50ui = (xi – 50)/ 10Frequency fifiui
25 – 3530-20-26-12
35 – 4540-10-110-10
45 – 55500080
55 – 65601011212
65 – 757020248
    N = 40Sum = -2

We have

A = 50, h = 10

Mean    = A + h (sum/N)

= 50 + 10 (-2/ 40)

= 50 – 0.5

= 49.5

 

14.

Class interval:25-29     30-34     35-39     40-44     45-49     50-54     55-59
Frequency:        14           22           16           6              5              3              4

Sol: Let the assumed mean (A) = 42

Class intervalMid value xidi= xi – 42ui = (xi – 42)/ 5Frequency fifiui
25 – 2927-15-314-42
30 – 3432-10-222-44
35 – 3937-5-116-16
40 – 44420060
45 – 49475155
50 – 545210236
55 – 5957153412
    N = 70Sum = -79

We have

A = 42, h = 5

Mean = A + h (sum/N)

= 42 + 5 (-79/70)

= 42 – 79/14

= 36.357

 

15.For the following distribution, calculate mean using all suitable methods:

Size of item:1 – 4       4 – 9       9 – 16    16 – 20 
Frequency:6              12           26           20

Sol: By direct method

Class intervalMid value xiFrequency fifixi
1 – 42.5615
4 – 96.51218
9 – 1612.526325
16 – 2721.520430
  N = 64Sum = 848

Mean = (sum/N) + A

= 848/ 64

= 13.25

By assuming mean method

Let the assumed mean (A) = 65

Class intervalMid value xiui = (xi – A) =xi– 65Frequency fifiui
1 – 42.5-46-25
4 – 96.50120
9 – 1612.5626196
16 – 2721.51520300
   N = 64Sum = 432

Mean = A + sum/N

= 6.5 + 6.75

= 13.25

 

16.The weekly observation on cost of living index in a certain city for the year 2004 – 2005 are given below.      Compute the weekly cost of living index.

Cost of living indexNumber of studentsCost of living indexNumber of students
1400 – 150051700 – 18009
1500 – 1600101800 – 19006
1600 – 1700201900 – 20002

Sol: Let the assumed mean (A) = 1650

Class intervalMid value xi

di= xi – A

= xi ­– 1650

ui = (xi – 1650)

100

Frequency fifiui
1400 – 15001450-200-25-10
1500 – 16001550-100-110-10
1600 – 1700165000200
1700 – 18001750100199
1800 – 190018502002612
1900 – 20001950300326
    N = 52Sum = 7

We have

A = 16, h = 100

Mean = A + h (sum/N)

= 1650 + 100 (7/52)

= 1650 + (175/13)

= 21625/13

= 1663.46

 

17.The following table shows the marks scored by 140 students in an examination of a certain paper:

Marks:0-10       10-20     20-30     30-40     40-50
Number of students:20           24           40           36           20

Calculate the average marks by using all the three methods: direct method, assumed mean deviation and shortcut method.

Sol: (i) Direct method:

Class intervalMid value xiFrequency fifixi
0 – 10520100
10 – 201524360
20 – 3025401000
30 – 4035361260
40 – 504520900
  N = 140Sum = 3620

Mean    = sum/ N

= 3620/ 140

= 25.857

(ii)Assumed mean method:

Let the assumed mean = 25

Mean = A + (sum/ N)

Class intervalMid value xiui = (xi – A)Frequency fifiui
0 – 105-2020-400
10 – 2015-1024-240
20 – 30250400
30 – 40351036360
40 – 50452020400
   N = 140Sum = 120

Mean = A + (sum/ N)

= 25 + (120/ 140)

= 25 + 0.857

= 25.857

(iii)Step deviation method:

Let the assumed mean (A) = 25

Class intervalMid value xi

di= xi – A

 

= xi ­– 25

ui = (xi – 25)

 

10

Frequency fifiui
0 – 105-20-220-40
10 – 2015-10-124-24
20 – 302500400
30 – 40351013636
40 – 50452022040
    N = 140Sum = 12

Mean = A + h(sum/ N)

= 25 + 10(12/ 140)

= 25 + 0.857

= 25.857

 

18.The mean of the following frequency distribution is 62.8 and the sum of all the frequencies is 50. Compute the miss frequency f1 and f2.

Class:   0-20       20-40     40-60     60-80     80-100   100-120
Frequency:5              f1                   10           f2                   7              8

Sol:

Class intervalMid value xiFrequency fifixi
0 – 2010550
20 – 4030f130f1
40 – 605010500
60 – 8070f270f2
80 – 100907630
100 – 1201108880
  N = 50Sum = 30f1+70f2+ 2060

Given,

sum of frequency = 50

5 + f1 + 10 + f2 + 7 + 8 = 50

f1 + f2 = 20

3f1 + 3f2 = 60 —- (1) [multiply both side by 3]

And mean = 62.8

Sum/ N = 62.8

(30f1+70f2+ 2060)/ 50 = 62.8

30f1+70f2 = 3140 – 2060

30f1+70f2 = 1080

3f1 + 7f2 = 108 —- (2) [divide it by 10]

subtract equation (1) from equation (2)

3f1 + 7f2 – 3f1 – 3f2 = 108 – 60

4f2 = 48

f2 = 12

Put value of f2 in equation (1)

3f1 + 3(12) = 60

f1 = 24/3 = 8

f1 = 8, f2 = 12

 

19.The following distribution shows the daily pocket allowance given to the children of a multistory building. The average pocket allowance is Rs 18.00. Find out the missing frequency.

Class interval:11-13     13-15     15-17     17-19     19-21     21-23     23-25
Frequency:7              6              9              13           –              5              4

Sol: Given mean = 18,

Let the missing frequency be v

Class intervalMid value xiFrequency fifixi
11 – 1312784
13 – 1514688
15 – 17169144
17 – 191813234
19 – 2120x20x
21 – 23225110
23 – 2514456
  N =44 + xSum = 752 + 20x

Mean = sum/ N

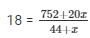
Ex-7.3 Statistics, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10

792 + 18x = 752 + 20x

2x = 40

x = 20

 

20.If the mean of the following distribution is 27. Find the value of p.

Class:   0-10       10-20     20-30     30-40     40-50
Frequency:8              p             12           13           10

Sol:

Class intervalMid value xiFrequency fifixi
0 – 105840
10 – 2015P152
20 – 302512300
30 – 403513455
40 – 504516450
  N = 43 + PSum = 1245 + 15p

Given mean =27

Mean = sum/ N

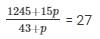
Ex-7.3 Statistics, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10

1245 + 15p = 1161 + 27p

12p = 84

P = 7

 

21.In a retail market, fruit vendors were selling mangoes kept in packing boxes. These boxes contain varying number of mangoes. The following was the distribution of mangoes according to the number of boxes.

Number of mangoes:50-52     53-55     56-58     59-61     62-64
Number of boxes:15           110         135         115         25

Find the mean number of mangoes kept in packing box. Which method of finding the mean did you choose?

Sol:

Number of mangoesNumber of boxes (fi)
50 – 5215
53 – 55110
56 – 58135
59 – 61115
62 – 6425

We may observe that class internals are not continuous

There is a gap between two class intervals. So we have to add ½  from lower class limit of each interval and class mark (xi) may be obtained by using the relation

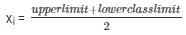
Ex-7.3 Statistics, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10

Class size (h) of this data = 3

Now taking 57 as assumed mean (a) we may calculated di ,ui, fiui as follows

Class intervalFrequency fi

Mid value xi

 

 

di= xi – A

 

= xi ­– 25

ui = (xi – 25)

 

10

fiui
49.5 – 52.51551-6-2-30
52.5 – 55.511054-3-1-110
55.5 – 58.513557000
58.5 – 61.51156031115
61.5 – 64.525636250
TotalN = 400   Sum = 25

Now we have N                = 400

Sum = 25

Mean = A + h (sum/ N)

= 57 + 3 (45/400)

= 57 + 3/ 16

= 57+ 0.1875

= 57.19

Clearly mean number of mangoes kept in packing box is 57.19

 

22.The table below shows the daily expenditure on food of 25 households in a locality

Daily expenditure (in Rs):100-150                150-200                200-250                250-300                300-350
Number of households:               4                              5                              12                           2                              2 

Find the mean daily expenditure on food by a suitable method.

Sol: we may calculate class mark (xi) for each interval by using the relation

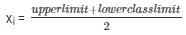
Ex-7.3 Statistics, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10

Class size = 50

Now, talking 225 as assumed mean (xi) we may calculate di ,ui, fiui as follows

Daily expenditureFrequency fiMid value xi di= xi ­– 225

ui = (xi – 225)

50

fiui
100 – 1504125-100-2-8
150 – 2005175-50-1-5
200 – 25012225000
250 – 30022755012
300 – 350232510024
 N = 25   Sum = -7

Now we may observe that

N = 25

Sum = -7

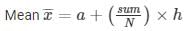
Ex-7.3 Statistics, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10

225 + 50 (-7/ 25)

225 – 14 = 211

So, mean daily expenditure on food is Rs 211

 

23.To find out the concentration of SO2 in the air (in parts per million i.e ppm) the data was collected for localities for 30 localities in a certain city and is presented below:

Concentration of SO2 (in ppm)Frequency
0.00 – 0.044
0.04 – 0.089
0.08 – 0.129
0.12 – 0.162
0.16 – 0.204
0.20 – 0.242

 Find the mean concentration of SO2 in the air

Sol: we may find class marks for each interval by using the relation

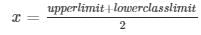
Ex-7.3 Statistics, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10

Class size of this data = 0.04

Now taking 0.04 assumed mean (xi) we may calculate di ,ui, fiui as follows

Concentration of SO2Frequency fi

Class interval xi

 

 

di = xi – 0.14uifiui
0.00 – 0.0440.02-0.12-3-12
0.04 – 0.0890.06-0.08-2-18
0.08 – 0.1290.10-0.04-1-9
0.12 – 0.1620.14000
0.16 – 0.2040.180.0414
0.20 – 0.2420.220.0824
TotalN = 30   Sum = -31

From the table we may observe that

N = 30

Sum = -31

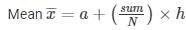
 Ex-7.3 Statistics, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10

= 0.14 +(0.04)(-31/30)

= 0.099 ppm

So mean concentration of SO2 ­in the air is 0.099 ppm

 

24.A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a student was absent.

Number of days:0-6          6-10       10-14     14-20     20-28     28-38     38-40
Number of students:11           10           7              4              4              3              1

Sol: We may find class mark of each interval by using the relation

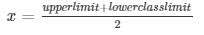
Ex-7.3 Statistics, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10

Now, taking 16 as assumed mean (a) we may

Calculate di and fidi  as follows

Number of daysNumber of students fiXid = xi + 10fidi
0 – 6113-13-143
6 – 10108-8-280
10 – 14712-4-28
14 – 2071600
20 – 28824832
28 – 363331751
30 – 401392323
TotalN = 40  Sum = -145

Now we may observe that

N = 40

Sum= -145

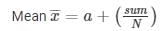
Ex-7.3 Statistics, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10

= 16 + (-145/ 40)

= 16 – 3.625

= 12.38

So mean number of days is 12.38 days, for which student was absent

 

25.The following table gives the literacy rate (in percentage) of 35 cities. Find the mean literacy rate.

Literacy rate (in %):45-55     55-65     65-75     75-85     85-95
Number of cites:3              10           11           8              3

Sol: We may find class marks by using the relation

Ex-7.3 Statistics, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10

Class size (h) for this data = 10

Now taking 70 as assumed mean (a) wrong

Calculate di ,ui, fiui as follows

Litracy rate (in %)Number of cities (fi)

Mid value xi

 

 

di= xi ­– 70

ui =  di

 

50

fiui
45 – 55350-20-2-6
55 – 651060-10-1-10
65 – 751170000
75 – 858801018
85 – 953902026
TotalN = 35   Sum = -2

Now we may observe that

N = 35

Sum = -2

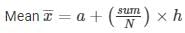
Ex-7.3 Statistics, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10

= 70 + (-2/35)

= 70 – 4/7

= 70 – 0.57

= 69.43

So, mean literacy rate is 69.43 %

 

The document Ex-7.3 Statistics, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 is a part of the Class 10 Course Extra Documents, Videos & Tests for Class 10.
All you need of Class 10 at this link: Class 10
5 videos|292 docs|59 tests
Join Course for Free

Top Courses for Class 10

FAQs on Ex-7.3 Statistics, Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10

1. What are RD Sharma Solutions?
Ans. RD Sharma Solutions are a set of comprehensive solutions provided for the RD Sharma textbook. These solutions are designed to help students understand and solve the different mathematical problems and exercises given in the book.
2. What is Ex-7.3 Statistics in RD Sharma Class 10 Maths?
Ans. Ex-7.3 Statistics is a chapter in the RD Sharma Class 10 Maths textbook that covers the topic of statistics. It includes concepts such as mean, median, mode, and graphical representation of data. This exercise provides various problems and exercises for students to practice and develop their understanding of statistics.
3. How can RD Sharma Solutions for Ex-7.3 Statistics help in exam preparation?
Ans. RD Sharma Solutions for Ex-7.3 Statistics can be extremely helpful in exam preparation. These solutions provide step-by-step explanations for solving the problems in the textbook. By referring to these solutions, students can understand the concepts and techniques required to solve statistical problems effectively. Practicing these solutions can also help students improve their problem-solving skills and increase their chances of scoring well in the exams.
4. Are the RD Sharma Solutions for Ex-7.3 Statistics available online?
Ans. Yes, RD Sharma Solutions for Ex-7.3 Statistics are available online. There are several websites and educational platforms that provide these solutions for free. Students can easily access these solutions and use them for reference and practice. They can also download these solutions in PDF format for offline use.
5. Can RD Sharma Solutions for Ex-7.3 Statistics be used for self-study?
Ans. Yes, RD Sharma Solutions for Ex-7.3 Statistics can be used for self-study. These solutions are designed to be easily understandable and comprehensive. By referring to these solutions, students can learn and practice the concepts of statistics on their own. They can solve the problems given in the textbook and then cross-check their solutions with the provided RD Sharma Solutions to assess their understanding and identify any mistakes. Self-study using these solutions can be a great way to reinforce concepts and prepare for exams.
Related Exams
About this Document
Dec 26, 2024 Last updated
Document Description: RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths for Class 10 2024 is part of Extra Documents, Videos & Tests for Class 10 preparation. The notes and questions for RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths have been prepared according to the Class 10 exam syllabus. Information about RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths covers topics like and RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths Example, for Class 10 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths.
Introduction of RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths in English is available as part of our Extra Documents, Videos & Tests for Class 10 for Class 10 & RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths in Hindi for Extra Documents, Videos & Tests for Class 10 course. Download more important topics related with notes, lectures and mock test series for Class 10 Exam by signing up for free. Class 10: Ex-7.3 Statistics, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10
Description
Full syllabus notes, lecture & questions for Ex-7.3 Statistics, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 - Class 10 | Plus excerises question with solution to help you revise complete syllabus for Extra Documents, Videos & Tests for Class 10 | Best notes, free PDF download
Information about RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths
In this doc you can find the meaning of RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths defined & explained in the simplest way possible. Besides explaining types of RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths theory, EduRev gives you an ample number of questions to practice RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths tests, examples and also practice Class 10 tests
5 videos|292 docs|59 tests
Join Course for Free
Download as PDF
Explore Courses for Class 10 exam

Top Courses for Class 10

Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
10M+ students study on EduRev
Related Searches

Exam

,

Class 10

,

mock tests for examination

,

Objective type Questions

,

Maths RD Sharma Solutions | Extra Documents

,

past year papers

,

Videos & Tests for Class 10

,

Ex-7.3 Statistics

,

Class 10

,

study material

,

Important questions

,

Maths RD Sharma Solutions | Extra Documents

,

ppt

,

Maths RD Sharma Solutions | Extra Documents

,

Previous Year Questions with Solutions

,

video lectures

,

Viva Questions

,

pdf

,

Summary

,

Semester Notes

,

Ex-7.3 Statistics

,

shortcuts and tricks

,

Class 10

,

Extra Questions

,

practice quizzes

,

Videos & Tests for Class 10

,

Sample Paper

,

Videos & Tests for Class 10

,

Ex-7.3 Statistics

,

MCQs

,

Free

;
Additional Information about RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths for Class 10 Preparation

RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths Free PDF Download

The RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths is an invaluable resource that delves deep into the core of the Class 10 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths now and kickstart your journey towards success in the Class 10 exam.

Importance of RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths

The importance of RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths cannot be overstated, especially for Class 10 aspirants. This document holds the key to success in the Class 10 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths Notes

RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths Notes on EduRev are your ultimate resource for success.

RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths Class 10 Questions

The "RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths Class 10 Questions" guide is a valuable resource for all aspiring students preparing for the Class 10 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths on the App

Students of Class 10 can study RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of RD Sharma Solutions - Ex-7.3 Statistics, Class 10, Maths is prepared as per the latest Class 10 syllabus.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup