Ex-5.1 Trigonometric Ratios(Part - 2), Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
3.) In the below figure, find tan P and cot R. Is tan P = cot R?
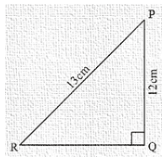
To find, tan P, cot R
Sol.
In the given right angled ΔPQR, length of side OR is unknown
Therefore , by applying Pythagoras theorem in ΔPQR
We get,
PR2 = PQ2 + QR2
Substituting the length of given side PR and PQ in the above equation
132 = 122 + QR2
QR2 = 132 – 122
QR2 = 169 – 144
QR2 = 25
QR = 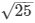
By definiton, we know that ,
tanP = Perpendicularsideoppositeto∠P/Basesideadjacentto∠P
tanP = QR/PQ
tanP = 5/12 …. (1)
Also, by definition, we know that
cotR = Basesideadjacentto∠R/Perpendicularsideoppositeto∠R
cotR = QR/PQ
cotR = 5/12 …. (2)
Comparing equation (1) ad (2), we come to know that that R.H.S of both the equation are equal.
Therefore, L.H.S of both equations is also equal
tan P = cot R
Answer:
Yes , tan P = cot R = 5/12
4.) If sin A = 9/41, Compute cos A and tan A.
Sol. Given: sinA = 9/41 …. (1)
To find: cos A, tan A
By definition,
sinA = Perpendicularsideoppositeto∠A/Hypotenuse …. (2)
By comparing (1) and (2)
We get ,
Perpendicular side = 9 and
Hypotenuse = 41
Now using the perpendicular side and hypotenuse we can construct ΔABC as shown below

Length of side AB is unknown is right angled ΔABC ,
To find the length of side AB, we use Pythagoras theorem,
Therefore, by applying Pythagoras theorem in ΔABC ,
We get,
AC2 = AB2 + BC2
412 = AB2 + 92
AB2 = 412 – 92
AB2 = 168 – 81
AB = 1600
AB = 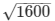
AB = 40
Hence, length of side AB = 40
Now
By definition,
cosA = Basesideadjacentto∠A/Hypotenuse
cosA = AB/AC
cosA = 40/41
Now,
By definition,
tanA = Perpendicularsideoppositeto∠A/Basesideadjacentto∠A
tanA = BC/AB
tanA = 9/40
Answer:
cosA = 40/41 , tanA = 9/40
5.) Given 15cot A = 8, find sin A and sec A.
Answer: Given: 15cot A = 8
To find: sin A, sec A
Since 15 cot A = 8
By taking 15 on R.H.S
We get,
cotA = 8/15
By definition,
cotA = 1/tanA
Hence,
cotA = 1Perpendicularsideoppositeto∠A/Basesideadjacentto∠A
cotA = Basesideadjacentto∠A/Perpendicularsideoppositeto∠A …. (2)
Comparing equation (1) and (2)
We get,
Base side adjacent to ∠A = 8
Perpendicular side opposite to ∠A = 15
ΔABC can be drawn below using above information
Hypotenuse side is unknown.
Therefore, we find side AC of ΔABC by Pythagoras theorem.
So, by applying Pythagoras theorem to ΔABC
We get,
AC2 = AB2 +BC2
Substituting values of sides from the above figure
AC2 = 82 + 152
AC2 = 64 + 225
AC2 = 289
AC = 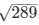
AC = 17
Therefore, hypotenuse = 17
Now by definition,
sinA = Perpendicularsideoppositeto∠A/Hypotenuse
Therefore, sinA = BC/AC
Substituting values of sides from the above figure
sinA = 1517
By definition,
secA = 1/cosA
Hence,
secA = 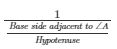
secA = Hypotenuse/Basesideadjacentto∠A
Substituting values of sides from the above figure
secA = 17/8
Answer:
sinA = 15/17, secA = 17/8
6.) In ΔPQR , right angled at Q, PQ = 4cm and RQ = 3 cm .Find the value of sin P, sin R , sec P and sec R.
Sol. Given:
ΔPQR is right angled at vertex Q.
PQ = 4cm
RQ = 3cm
To find,
sin P, sin R , sec P , sec R
Given ΔPQR is as shown below
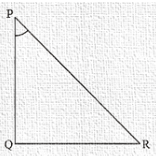
Hypotenuse side PR is unknown.
Therefore, we find side PR of ΔPQR by Pythagoras theorem
By applying Pythagoras theorem to ΔPQR
We get,
PR2 = PQ2 +RQ2
Substituting values of sides from the above figure
PR2 = 42 +32
PR2 = 16 + 9
PR2 = 25
PR = 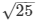
PR = 5
Hence, Hypotenuse = 5
Now by definition,
sinP = Perpendicularsideoppositeto∠P/Hypotenuse
sinP = RQ/PR
Substituting values of sides from the above figure
sinP = 3/5
Now by definition,
sinR = Perpendicularsideoppositeto∠R/Hypotenuse
sinR = PQ/PR
Substituting the values of sides from above figure
sinR = 4/5
By definition,
secP = 1/cosP
secP = 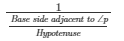
secP = Hypotenuse/Basesideadjacentto∠P
Substituting values of sides from the above figure
secP = PR/PQ
secP = 5/4
By definition,
secR = 1/cosR
secR = 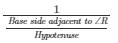
secR = Hypotenuse/Basesideadjacentto∠R
Substituting values of sides from the above figure
secR = PR/RQ
secR = 5/3
Answer:
sinP = 3/5 , sinR = 4/5,
secP = 5/4, secR = 5/3
7.) If cotΘ = 7/8, evaluate
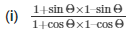
(ii) cot2Θ
Sol. Given: cotΘ = 7/8
To evaluate: 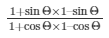
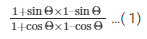
We know the following formula
(a + b)(a – b) = a2 – b2
By applying the above formula in the numerator of equation (1)
We get,
(1+sinθ)×(1–sinθ) = 1–sin2θ.....(2)(Where,a = 1andb = sinθ)
Similarly,
By applying formula (a +b) (a – b) = a2 – b2 in the denominator of equation (1).
We get,
(1+cosΘ)(1–cosΘ) = 12–cos2Θ … (Where a = 1 and b = cosΘ
(1+cosΘ)(1–cosΘ) = 1–cos2Θ … (Where a = 1 and b = cosΘ
Substituting the value of numerator and denominator of equation (1) from equation (2), equation (3).
Therefore,
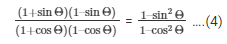
Since,
cos2Θ + sin2Θ = 1
Therefore,
cos2Θ = 1–sin2 Θ
Also, sin2Θ = 1–cos2Θ
Putting the value of 1–sin2Θ and 1–cos2Θ in equation (4)
We get,
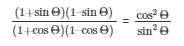
We know that, 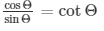
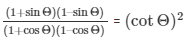
Since, it is given that cotΘ = 7/8
Therefore,
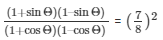
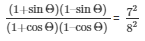
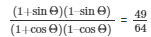
(ii) Given: cotΘ = 7/8
To evaluate: cot2Θ
cotΘ = 7/8
Squaring on both sides,
We get,
(cotΘ)2 = (7/8)2
(cotΘ)2 = 49/64
Answer:
49/64
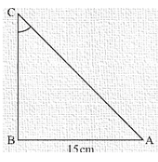
8.) If 3cotA = 4 , check whether 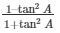 = cos2A – sin2A or not.
= cos2A – sin2A or not.
Sol. Given: 3cot A = 4
To check whether 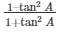 = cos2A – sin2A or not.
= cos2A – sin2A or not.
3cot A = 4
Dividing by 3 on both sides,
We get,
cot A = 4/3 …. (1)
By definition,
cotA = 1/tanA
Therefore,
cotA =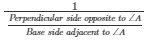
cotA = Basesideadjacentto∠A/Perpendicularsideoppositeto∠A …. (2)
Comparing (1) and (2)
We get,
Base side adjacent to ∠A = 4
Perpendicular side opposite to ∠A = 3
Hence ΔABC is as shown in figure below
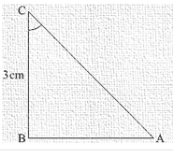
In ΔABC , Hypotenuse is unknown
Hence, it can be found by using Pythagoras theorem
Therefore by applying Pythagoras theorem inΔABC
We get
AC2 = AB2 +BC2
Substituting the values of sides from the above figure
AC2 = 42 + 32
AC2 = 16 +9
AC2 = 25
AC = 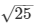
AC = 5
Hence, hypotenuse = 5
To check whether
To check whether 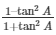 = cos2A–sin2A or not.
= cos2A–sin2A or not.
We get thee values of tan A , cos A , sin A
By definition,
tan A = 1/cotA
Substituting the value of cot A from equation (1)
We get,
tan A = 1/4
tan A = 3/4 …. (3)
Now by definition,
cosA = Basesideadjacentto∠A/Hypotenuse
cosA = AB/AC
Substituting the values of sides from the above figure
cosA = 4/5 …. (5)
Now we first take L.H.S of equation 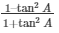 = cos2A – sin2A
= cos2A – sin2A
L.H.S = 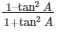
Substituting value of tan A from equation (3)
We get,
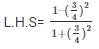
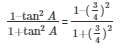
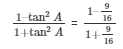
Taking L.C.M on both numerator and denominator
We get,
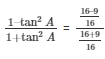
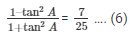
Now we take R.H.S of equation whether 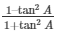 = cos2A–sin2A
= cos2A–sin2A
R.H.S = cos2A – sin2A
Substituting value of sin A and cos A from equation (4) and (5)
We get,
R.H.S = 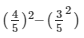
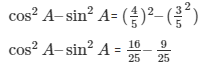
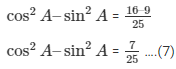
Comparing (6) and (7)
We get.
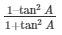 = cos2A–sin2A
= cos2A–sin2A
Answer:
Yes, 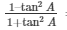 = cos2A–sin2A
= cos2A–sin2A
9.) If tanΘ = ab , find the value of 
Sol.
Given:
tanΘ = a/b …. (1)
Now, we know that tanΘ = sinΘ/cosΘ
Therefore equation (1) become as follows
sinΘ/cosΘ = a/b
Now, by applying invertendo
We get,
cosΘ/sinΘ = b/a
Now by applying Componendo – dividendo
We get,
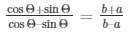
Therefore,
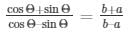
10.) If 3tanΘ = 4 , find the value of 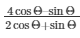
Sol.
Given: If 3tanΘ = 4
Therefore,
tanΘ = 4/3 …. (1)
Now, we know that tanΘ = sinΘ/cosΘ
Therefore equation (1) becomes
sinΘ/cosΘ = 4/3 ….(2)
Now, by applying Invertendo to equation (2)
We get,
cosΘ/sinΘ = 3/4 …. (3)
Now, multiplying by 4 on both sides
We get
4×cosΘ/sinΘ = 4×3/4
Therefore

Now, multiplying by 2 on both sides of equation (3)
We get,
2cosΘ/sinΘ = 3/2
Now by applying componendo in above equation
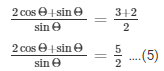
We get,

Therefore,
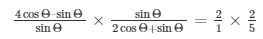
Therefore, on L.H.S sinΘ cancels and we get,
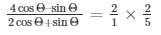
Therefore,
4cosΘ–sinΘ = 4
11.) If 3cotΘ = 2, find the value of 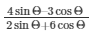 Sol.
Sol.
Given:
3cotΘ = 2
Therefore,
cotΘ = 2/3 …. (1)
Now, we know that cotΘ = cosΘ/sinΘ
Therefore equation (1) becomes
cosΘ/sinΘ = 2/3 ….(2)
Now , by applying invertendo to equation (2)
sinΘ/cosΘ = 3/2 ….(3)
Now, multiplying by 43 on both sides,
We get,
4/3 × sinΘ/cosΘ = 4/3 × 3/2
Therefore, 3 cancels out on R.H.S and
We get,
4sinΘ/3cosΘ = 2/1
Now by applying invertendo dividendo in above equation
We get,
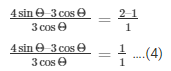
Now, multiplying by 2/6 on both sides of equation (3)
We get,
2/6 × sinΘ/cosΘ = 2/6 × 3/2
Therefore, 2 cancels out on R.H.S and
We get,
2sinΘ/6cosΘ = 3/6
2sinΘ/6cosΘ = 1/2
Now by applying componendo in above equation
We get,
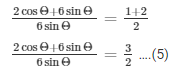
Now, by dividing equation (4) by (5)
We get,
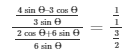
Therefore,

Therefore, on L.H.S (3 sinΘ) cancels out and we get,
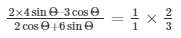
Now, by taking 2 in the numerator of L.H.S on the R.H.S
We get,
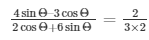
Therefore, 2 cancels out on R.H.S and
We get,
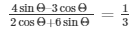
Hence answer,
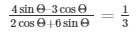
|
5 videos|292 docs|59 tests
|
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















