Ex-5.1 Trigonometric Ratios (Part - 4), Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
23.) If 8tanA = 15 , find sinA–cosA
Sol. Given:
8tanA = 15
Therefore,
tanA = 15/8 …. (1)
To find:
sinA–cosA
Now we know tan A is defined as follows
tanA = Perpendicular side opposite to∠A/Base side adjacent to∠A …. (2)
Now by comparing equation (1) and (2)
We get
Perpendicular side opposite to ∠A = 15
Base side adjacent to ∠A = 8
Therefore triangle representing angle A is as shown below
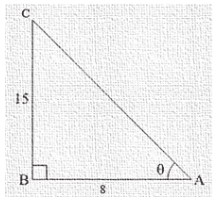
Side AC = is unknown and can be found by using Pythagoras theorem
Therefore,
AC2 = AB2 + BC2
Now by substituting the value of known sides from figure (a)
We get,
AC2 = 152 + 82
AC2 = 225 + 64
AC = 289
Now by taking square root on both sides
We get,
AC = 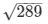
AC = 17
Therefore Hypotenuse side AC = 17 …. (3)
Now we know, sin A is defined as follows
sinA = Perpendicular side opposite to∠AHypotenuse
Therefore from figure (a) and equation (3)
We get,
sinA = BC/AC
sinA = 15/17 …. (4)
Now we know, cos A is defined as follows
cosA = Base side adjacent to∠A/Hypotenuse
Therefore from figure (a) and equation (3)
We get,
cosA = AB/AC
cosA = 8/17 …. (5)
Now we find the value of expression sinA–cosA
Therefore by substituting the value the value of sinA and cosA from equation (4) and (5) respectively , we get,
sinA–cosA = 15/17–8/17
sinA–cosA = 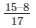
sinA–cosA = 7/17
Hence, sinA–cosA = 7/17
24.) If tanΘ = 20/21, show that 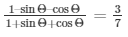
Sol.
Given:
tanΘ = 20/21
To show that 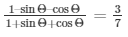
Now we know that
tanΘ = Perpendicular side opposite to∠Θ/Base side adjacent to∠Θ
Therefore,
tanΘ = 20/21
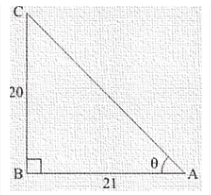
Side AC be the hypotenuse and can be found by applying Pythagoras theorem
Therefore,
AC2 = AB2 + BC2
AC2 = 212 + 202
AC2 = 441 + 400
AC2 = 841
Now by taking square root on both sides
We get,
AC = 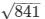
AC = 29
Therefore Hypotenuse side AC = 29
Now we know, sinΘ is defined as follows,
sinAΘ = Perpendicular side opposite to∠Θ/Hypotenuse
Therefore from figure and above equation
We get,
sinΘ = AB/AC
sinΘ = 20/29
Now we know cosΘ is defined as follows
cosΘ = Base side adjacent to∠Θ/Hypotenuse
Therefore from figure and above equation
We get,
cosΘ = AB/AC
cosΘ = 21/29
Now we need to find the value of expression 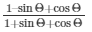
Therefore by substituting the value of sinΘ and cosΘfrom above equations, we get

Therefore after evaluating we get,

Hence,

25.) If cosecA = 2 , find 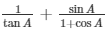
Sol. Given:
cosecA = 2
To find 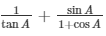
Now cosec A = Hypotenuse/Oppositeside = 2/1
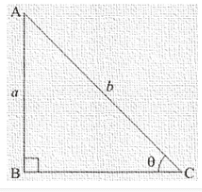
Here BC is the adjacent side,
By applying Pythagoras theorem,
AC2 = AB2 + BC2
4 = 1 + BC2
BC2 = 3
BC = √3
Now we know that
sinA = 1/cosecA
sinA = 1/2 …. (1)
tanA = AB/BC
tanA = 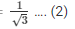
cosA = BC/AC
cosA = 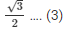
Substitute all the values of sinA , cosA and tanA from the equations(1) ,(2) and (3) respectively
We get.
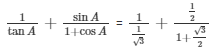
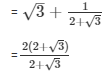
= 2
Hence,
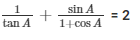
26.) If ∠A and ∠B are acute angles such that cos A = cos B , then show that ∠A = ∠B
Sol. Given:
∠A and ∠B are acute angles
cos A = cos B such that ∠A = ∠B
Let us consider right angled triangle ACB
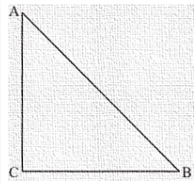
Now since cos A = cos B
Therefore
AC/AB = BC/AB
Now observe that denominator of above equality is same that is AB
Hence AC/AB = BC/AB only when AC = BC
Therefore AC = BC
We know that when two sides of triangle are equal, then opposite of the sides are also
Equal.
Therefore
We can say that
Angle opposite to side AC = angle opposite to side BC
Therefore,
∠B = ∠A
Hence, ∠A = ∠B
27.) In a ΔABC , right angled triangle at A, if tan C = √3 , find the value of sin B cos C + cos B sin C.
Sol. Given:
ΔABC
To find : sin B cos C + cos B sin C
The given a ΔABC is as shown in figure
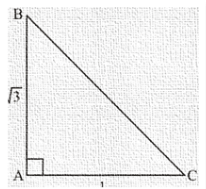
Side BC is unknown and can be found using Pythagoras theorem,
Therefore,
BC2 = AB2 + AC2
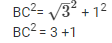
BC2 = 4
Now by taking square root on both sides
We get,
BC = √4
BC = 2
Therefore Hypotenuse side BC = 2 …. (1)
Now, sin B = Perpendicular side opposite to∠BHypotenuse
Therefore,
sinB = ACBC
Now by substituting the values from equation (1) and figure
We get,
sin B = 1/2 …. (2)
Now, cos B = Base side adjacent to∠BHypotenuse
Therefore,
cos B = AB/BC
Now substituting the value from equation
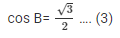
Similarly
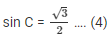
Now by definition,
tanC = sinC/cosC
So by evaluating
cosC = 1/2 …. (5)
Now, by substituting the value of sinB, cosB,sin C and cosC from equation (2) ,(3) ,(4) and (5) respectively in sinB cosC + cosB sin C
sinB cosC + cosB sin C = 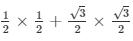
= 1/4 + 3/4
= 1
Hence,
sinB cosC + cosB sin C = 1
28.) State whether the following are true or false. Justify your answer.
(i) The value od tan A is always less than 1.
(ii) sec A = 12/5 for some value of ∠A.
(iii) cos A is the abbreviation used for the cosecant of ∠A.
(iv) sinΘ = 4/3 for some angle Θ.
Sol.
(i) tan A < 1
Value of tan A at 45o i.e… tan 45 = 1
As value os A increases to 90o
Tan A becomes infinite
So given statement is false.
(ii) sec A = 12/5 for some value of angle if
M-I
sec A = 2.4
sec A > 1
So given statements is true.
M- II
For sec A = 12/5 we get adjacent side = 13
Subtending 9i at B.
So, given statement is true.
(iii) Cos A is the abbreviation used for cosecant of angle A.
The given statement is false.
As such cos A is the abbreviation used for cos of angle A , not as cosecant of angle A.
(iv) Cot A is the product of cot A and A
Given statement is false
∵ cot A is a co-tangent of angle A and co-tangent of angle A = adjacent side/Oposite side.
(v) sinΘ = 4/3 for some angle Θ.
Given statement is false
Since value of sinΘ is less than(or) equal to one.
Here value of sinΘ exceeds one,
So given statement is false.
29.) If sinΘ = 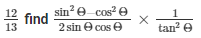
Sol.
Given: sinΘ = 12/13
To Find: 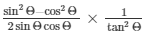
As shown in figure
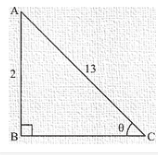
Here BC is the adjacent side,
By applying Pythagoras theorem,
AC2 = AB2 + BC2
169 = 144 + BC2
BC2 = 169 – 144
BC2 = 25
BC = 5
Now we know that,
cosΘ = Base side adjacent to∠Θ/Hypotenuse
cosΘ = BC/AC
cosΘ = 5/13
We also know that,
tanΘ = sinΘ/cosΘ
Therefore, substituting the value of sinΘ and cosΘ from above equations
We get,
tanΘ = 12/5
Now substitute all the values of sinΘ , cosΘ and tanΘ from above equations in 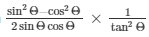
We get,
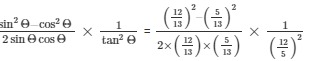
Therefore by further simplifying we get,
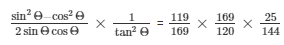
Therefore,
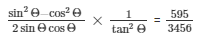
Hence,
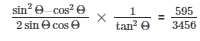
30.) If cosΘ = 5/13, find the value of 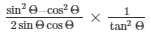
Sol. Given: If cosΘ = 5/13
To find:
The value of expression 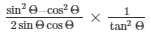
Now we know that
cosΘ = Base side adjacent to∠Θ/Hypotenuse …. (2)
Now when we compare equation (1) and (2)
We get,
Base side adjacent to ∠Θ = 5
Hypotenuse = 13
Therefore, Triangle representing ∠Θ is as shown below
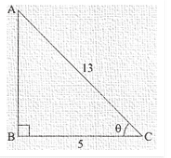
Perpendicular side AB is unknown and it can be found by using Pythagoras theorem
Therefore by applying Pythagoras theorem
We get,
AC2 = AB2 + BC2
Therefore by substituting the values ogf known sides,
AB2 = 132 – 52
AB2 = 169 -25
AB2 = 144
AB = 12 …. (3)
Now we know from figure and equation,
sinΘ = 12/13 …. (4)
Now we know that,
tanΘ = sinΘ/cosΘ
tanΘ = 12/5 …. (5)
Now w substitute all the values from equation (1), (4) and (5) in the expression below,
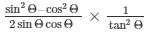
Therefore
We get,
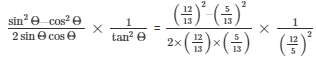
Therefore by further simplifying we get,
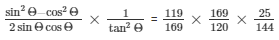
Therefore,
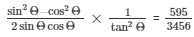
Hence,
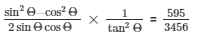
31.) If sec A = 17/8 , verify that 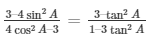
Sol. Given: sec A = 17/8
To verify: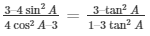
Now we know that cosA = 1secA
Now, by substituting the value of sec A
We get,
cosA = 8/17
Now we also know that,
sin2A + cos2A = 1
Therefore
sin2A = 1–cos2A
= (8/17)2
= 225/289
Now by taking square root on both sides,
We get,
sinA = 15/17
We also know that , tanA = sinA/cosA
Now by substituting the value of all the terms ,
We get,
tanA = 15/8
Now from the expression of above equation which we want to prove:
L.H.S = 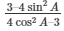
Now by substituting the value of cos A ad sin A from equation (3) and (4)
We get,
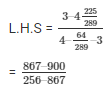
= 33/611
From expression
R.H.S = frac3–tan2A1–3tan2A
Now by substituting the value of tan A from above equation
We get,
R.H.S = 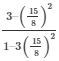
= 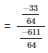
= 33/611
Therefore,
We can see that,
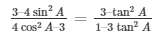
32.) If sinΘ = 3/4, prove that 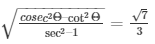
Sol. Given: sinΘ = 3/4 …. (1)
To prove:
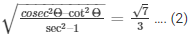
By definition,
sin A = Perpendicular side opposite to∠A/Hypotenuse …. (3)
By comparing (1) and (3)
We get,
Perpendicular side = 3 and
Hypotenuse = 4
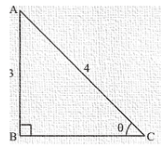
Side BC is unknown.
So we find BC by applying Pythagoras theorem to right angled ΔABC
Hence,
AC2 = AB2 + BC2
Now we substitute the value of perpendicular side (AB) and hypotenuse (AC) and get the base side (BC)
Therefore,
42 = 32 + BC2
BC2 = 16 – 9
BC2 = 7
BC = √7
Hence, Base side BC = √7 …. (3)
Now cos A = BC/AC

Now , cosecA = 1sinA
Therefore, from fig and equation (1)
cosecA = Hypotenuse/Perpendicular
cosecA = 4/3 …. (5)
Now, similarly
secA =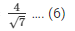
Further we also know that
cotA = cosA/sinA
Therefore by substituting th values from equation (1) and (4),
We get,
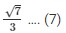
Now by substituting the value of cosec A, sec A and cot A from the equations (5), (6), and (7) in the L.H.S of expression (2)
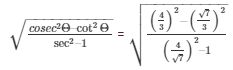
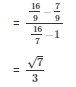
Hence it is proved that,
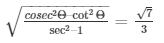
33.) If secA = 17/8 , verify that 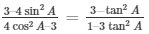
Sol. Given: secA = 17/8 …. (1)
To verify:
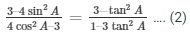
Now we know that sec A = 1/cosA
Therefore cosA = 1/secA
We get,
cosA = 8/17 …. (3)
Similarly we can also get,
sin A = sinA = 15/17 …. (4)
An also we know that tanA = sinAcosA
tanA = 15/8 …. (5)
Now from the expression of equation (2)
L.H.S: Missing close brace
Now by substituting the value of cos A and sin A from equation (3) and (4)
We get,
L.H.S = 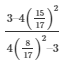
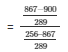
= 33/611 …. (6)
R.H.S = 
Now by substituting the value of tan A from equation (5)
We get,
R.H.S = 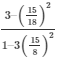
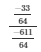
= 33/611 …. (7)
Now by comparing equation (6) and (7)
We get,
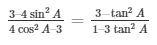
34.) If cotΘ = 3/4, prove that 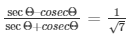
Sol.
Given: cotΘ = 3/4
Prove that: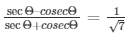
Now we know that
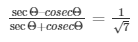
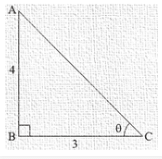
Here AC is the hypotenuse and we can find that by applying Pythagoras theorem
AC2 = AB2 + BC2
AC2 = 16 + 9
AC2 = 25
AC = 5
Similarly
secΘ = AC/BC
secΘ = 5/3
cosec = AC/AB
cosec = 5/4
Now on substituting the values in equations we get,
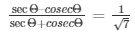
Therefore,
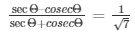
35.) If 3cosΘ–4sinΘ = 2cosΘ + sinΘ ,find tanΘ
Sol.
Given: 3cosΘ–4sinΘ = 2cosΘ + sinΘ
To find: tanΘ
We can write this as:
3cosΘ–4sinΘ = 2cosΘ + sinΘ
cosΘ = 5sinΘ
Dividing both the sides by cosΘ ,
We get,
cosΘ/cosΘ = 5sinΘ/cosΘ
1 = 5tanΘ
tanΘ = 1
Hence,
tanΘ = 1
36.) If ∠A and ∠P are acute angles such that tan A = tan P, then show ∠A = ∠P
Sol.
Given: A and P are acute angles tan A = tan P
Prove that: ∠A = ∠P
Let us consider right angled triangle ACP
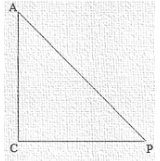
We know tanΘ = oppositeside/adjacentside
tan A = PC/AC
tan P = AC/PC
∴ tan A = tan P
PC/AC = AC/PC
PC = AC [∵Angle opposite to equal sides are equal]
∠A = ∠P<
|
5 videos|292 docs|59 tests
|
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















