Ex-5.3 Trigonometric Ratios, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Q.1) Evaluate the following : (i) sin20/cos70
Sol (i) : Given that, sin20/cos70
Since sin (90 – Θ) = cosΘ
⇒ sin20/cos70 = sin(90 − 70)/cos70
⇒ sin20/cos70 = cos70/cos70
⇒ sin20/cos70 = 1
Therefore sin20/cos70 = 1
(ii) cos19/sin71
Sol.(ii): Given that, cos19/sin71
⇒ cos19/sin71 = cos(90 − 71)/sin71
⇒ cos19/sin71 = sin71/sin71
⇒ cos19/sin71 = 1
Since cos(90-Θ) = sin Θ
Therefore cos19/sin71 = 1
(iii) sin21/cos69
Sol.(iii): Given that, sin21/cos69
Since (90-Θ) = cosΘ
⇒ sin21/cos69 = sin(90 − 69)/cos69
⇒ sin21/cos69 = cos69/cos69
⇒ sin21/cos69 = 1
(iv) tan10/cot80
Sol.(iv): We are given that, tan10/cot80
Since tan(90-Θ) = cotΘ
⇒ tan10cot80 = tan(90 − 80)/cot80
⇒ tan10/cot80 =
cot80/cot80
⇒ tan10/cot80 = 1
Therefore tan10/cot80 = 1
(v) sec11/cosec79
Sol.(v):
Given that, sec11/cosec79
Since sec(90-Θ) = cosecΘ
⇒ sec11/cosec79 = sec(90 − 79)/cosec79
⇒ sec11/cosec79 = cosec79/cosec79
⇒ sec11/cosec79 = 1
Therefore sec11/cosec79 = 1
Q.2: EVALUATE THE FOLLOWING :
(i) (sin49°/cos41°)2 + (cos41°/sin49°)2
Sol.(i):
We have to find: (sin49°/cos41°)2 + (cos41°/sin49°)2
Since sec70°/cosec20° + sin59°/cos31° sin(90° – Θ) = cosΘ and cos(90° – Θ) = sinΘ
So
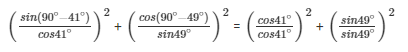
= 1 + 1 = 2
So value of (sin49°/cos41°)2 + (cos41°/sin49°)2 is 2
(ii) cos48° – sin42°
Sol.(ii)
We have to find: cos48° – sin42°
Since cos(90° − Θ) = sinΘ.So
cos48° – sin42° = cos(90° − 42°) − sin42°
= sin42° – sin42° = 0
So value of cos48° – sin42° is 0
(iii) cot40°/tan50° − 1/2(cos35°/sin55°)
Sol.(iii)
We have to find:
cot40°/tan50° − 1/2(cos35°/sin55°)
Since cot(90° − Θ) = tanΘ and cos(90° − Θ) = sinΘ
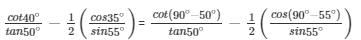
= tan50°/tan50° − 1/2(sin55°/sin55°)
= 1 − 1/2 = 1/2
So value of cot40°/tan50° − 1/2(cos35°/sin55°) is 1/2
(iv)(sin27°/cos63°)2 – (cos63°/sin27°)2
Sol(iv)
We have to find: (sin27°/cos63°)2 – (cos63°/sin27°)2
Since sin (90° − Θ) = cosΘ and cos (90° − Θ) = sinΘ
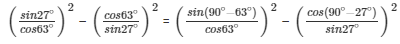
= (cos63°/cos63°)2 – (sin27°/sin27°)2 = 1-1 = 0
So value of (sin27°/cos63°)2 – (cos63°/sin27°)2 is 0
(v)tan35°/cot55° + cot78°/tan12° − 1
Sol.(v)
We have to find:
tan35°/cot55° + cot78°/tan12° − 1
Since tan (90° − Θ) = cotΘ and cot (90° − Θ) = tanΘ = 1
So value of tan35°/cot55° + cot78°/tan12°is1
(vi) sec70°/cosec20° + sin59°/cos31°
Sol.(vi)
We have to find: sec70°/cosec20° + sin59°/cos31°
Since sec70°/cosec20° + sin59°/cos31°and sec(90° − Θ) = cosecΘ
So
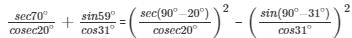
= cosec20°/cosec20° + cos31°/cos31° = 1 + 1 = 2
So value of sec70°/cosec20° + sin59°/cos31° is 2
(vii) cosec31° − sec59°.
Sol(vii)
We have to find: cosec31° − sec59°
Since cosec(90° − Θ) = secΘ.
So
= cosec31° − sec59°
= cosec(90° − 59°) − sec59 = sec59° − sec59° = 0
So value of cosec31° − sec59° is 0
(viii)(sin72° + cos18°) (sin72° − cos18°)
Sol.(viii)
We have to find: (sin72° + cos18°) (sin72° − cos18°)
Since sin(90° − Θ) = cosΘ,So
(sin72° + cos18°) (sin72° − cos18°) = (sin72°)2–(cos18°)2
= [sin(90° − 18°)]2 − (cos18°)2
= (cos18°)2– (cos18°)2
= cos218° − cos218° = 0
So value of (sin72° + cos18°) (sin72° − cos18°) is 0.
(ix) sin35°/sin55°–cos35°/cos55°
Sol(ix)
We find :
sin35°/sin55°–cos35°/cos55°
Since sin(90° − Θ) = cosΘ and cos(90° − Θ) = sinΘ
sin35°/sin55°–cos35°/cos55° = sin(90° − 55°)sin55°–cos(90° − 55°)cos55° = 1-1 = 0
So value of sin35°/sin55°–cos35°/cos55° is 0
(x) tan48°tan23°tan42°tan67°
Sol.(x)
We have to find tan48°tan23°tan42°tan67°
Since tan(90° − Θ) = cotΘ.
So
tan48°tan23°tan42°tan67° = tan(90° − 42°)tan(90° − 67°)tan42°tan67°
= cot42°cot67°tan42°tan67°
= (tan67°cot67°)(tan42°cot42°) = 1×1 = 1
So value of tan48°tan23°tan42°tan67° is 1
(xi)sec50°sin40° + cos40°cosec50°
Sol.(xi)
We have to find sec50°sin40° + cos40°cosec50°
Since cos(90° − Θ) = sinΘ,sec(90° − Θ) = cosecΘ and sinΘ.cosecΘ = 1.
So
sec50°sin40° + cos40°cosec50° = sec(90° − 40°)sin40° + cos(90° − 50°)cosec50° = 1 + 1 = 2
So value of sec50°sin40° + cos40°cosec50° is 2.
Q.3) Express cos75° + cot75° in terms of angle between 00 and 30°.
Sol. 3 :
Given that: cos75° + cot75°
= cos75° + cot75°
= cos(90° − 15°) + cot(90° − 15°)
= sin 15° + tan 15°
Hence the correct answer is sin 15° + tan 15°
Q.4) If sin3A = cos(A – 260), where 3A is an acute angle, find the value of A.
Sol.4:
We are given 3A is an acute angle
We have: sin3A = cos(A-26°)
⇒ sin3A = sin(90°-(A-26°))
⇒ sin3A = sin(116°-A)
⇒ 3A = 116°-A
⇒ 4A = 116°
⇒ A = 29°
Hence thecorrect answer is 29°
Q.5)If A, B, C are the interior angles of a triangle ABC, prove that,
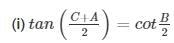
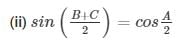
Sol.5:
(i)We have to prove: tan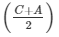 = cotB/2
= cotB/2
Since we know that in triangle ABC
A + B + C = 180
⇒ C + A = 180°-B
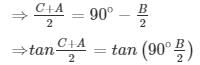
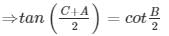
Hence proved
(ii)We have to prove : sin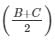 = cosA/2
= cosA/2
Since we know that in triangle ABC
A + B + C = 180
⇒ B + C = 180°-A
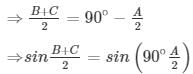
sin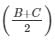 = cosA/2
= cosA/2
Hence proved
Q.6)Prove that :
(i)tan20°tan35°tan45°tan55°tan70° = 1
(ii)sin48°.sec48° + cos48°.cosec42° = 2
(iii) sin70°/cos20° + cosec20°/sec70° − 2cos70°.cosec20° = 0
(iv) cos80°/sin10° + cos59°.cosec31° = 2
Sol.6:
(i)Therefore
tan20°tan35°tan45°tan55°tan70°
= tan(90°–70°) tan(90°–55°) tan45°tan55°tan70°
= cot70°cot55°tan45°tan55°tan70°
= (tan70°cot70°)(tan55°cot55°)tan45°
= 1x1x1 = 1
Hence proved
(ii) We will simplify the left hand side
sin48°.sec48° + cos48°.cosec42° = sin48°. sec(90° − 48°)cos48°.cosec(90° − 48°)
= sin48°.cos48° + cos48°.sin48°
= 1 + 1 = 2
Hence proved
(iii) We have,sin70°/cos20° + cosec20°/sec70° − 2cos70°.cosec20° = 0
So we will calculate left hand side
sin70°/cos20° + cosec20°/sec70° − 2cos70°.cosec20° = 0 = sin70°/cos20° + cos70°sin20° − 2cos70°.cosec(90° − 70°)
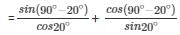 –2cos70°.cosec(90° − 70°)
–2cos70°.cosec(90° − 70°)
= cos20°/cos20° + sin20°/sin20° − 2×1 = 1 + 1-2 = 2-2 = 0
Hence proved
(iv)We have cos80°/sin10° + cos59°.cosec31° = 2
We will simplify the left hand side
cos80°/sin10° + cos59°.cosec31° = 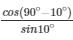 + cos59°.cosec(90° − 59°)
+ cos59°.cosec(90° − 59°)
= sin10°/sin10° + cos59°.sec59° = 1 + 1 = 2
Hence proved.
Question 7.
If A,B,C are the interior of triangle ABC , show that
(i) sin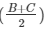 = cosA/2
= cosA/2
Sol.
A + B + C = 1800
B + C = 1800– A/2
LHS = RHS
(ii)cos(90° − A/2) = sinA/2
LHS = RHS
Question 8
If 2Θ + 45°and30 − Θ are acute angles , find the degree measure of
Θ satisfying sin(20 + 45°) = cos(30° + Θ)
Sol. Here 20 + 45° = sin(60° + Θ)
We know that ,((90° − Θ) = cos(Θ)
= sin(2Θ + 45°) = sin(90° − (30° − Θ))
= sin(2Θ + 45°) = sin(90° − 30° − Θ)
= sin(2Θ + 45°) = sin(60° + Θ)
On equating sin of angle of we get,
= 2Θ + 45° = 60° + Θ = Θ = 15°
Question 9
If Θ is appositive acute angle such that secΘ = csc60° , find
2cos2Θ − 1
Sol.
We know that, sec(90° − Θ) = csc2Θ
= sec(Θ) = sec(90° − 60°)
= Θ = 30° = 2cos2Θ − 1
= 2cos230 − 1
= 2(√3/2)2 − 1
= 2(3/4) − 1 = (3/2) − 1 = (1/2)
Q10.If sin3Θ = cos(Θ − 6°) where 3ΘandΘ − 6circ acute angles, find the value of Θ.
Sol:
We have, sin3Θ = cos(Θ − 6°)
cos(90° + 3Θ) = cos(Θ − 6°)
90°–3Θ = Θ–6°
− 3Θ − Θ = 6° − 90°
− 4Θ = 96°
Θ = − 96°/ − 4 = 24°
Q11.If sec2A = csc(A − 42°) where 2A is acute angle, find the value of A.
Sol:we know that sec(90 − 3Theta) = cscΘ
sec2A = sec(90–(A − 42))
sec2A = sec(90–A + 42))
sec2A = sec(132–A))
Now equating both the angles we get
2A = 132 – A
A = = 132/3
A = 44
|
5 videos|292 docs|59 tests
|
FAQs on Ex-5.3 Trigonometric Ratios, Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. What are the trigonometric ratios in mathematics? |  |
| 2. How do you find the value of trigonometric ratios? |  |
| 3. What is the range of trigonometric ratios? |  |
| 4. How are trigonometric ratios used in real-life applications? |  |
| 5. Can trigonometric ratios be negative? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















