Ex-6.2 Trigonometric Identities, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Q1) If cosθ = 45, find all other trigonometric ratios of angle Θ.
Solution:
We have:
sinΘ = 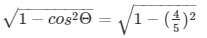
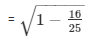
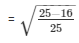
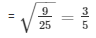
Therefore, sinΘ = 3/5
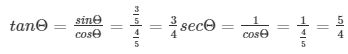
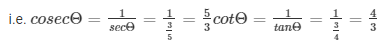
Q2) If sinΘ = 1/√2, find all other trigonometric ratios of angle Θ.
Solution:
We have,
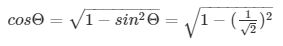
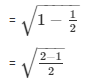
= cosΘ = 1/√2
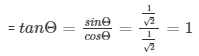
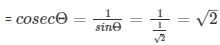
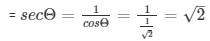
= cotΘ = 1/tanΘ = 1/1 = 1
Q3) If tanΘ = 1/√2, find the value of 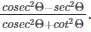
Solution:
We know that secΘ =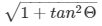
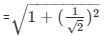
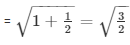
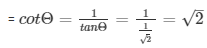
= cosecΘ = 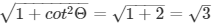
Substituting it in equation (1) we get
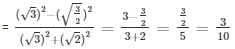
Q4) If tanΘ = 3/4, find the value of 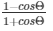
Solution:
We know that
secΘ = 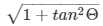
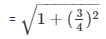
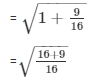
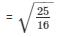
= secΘ = 5/4
= secΘ =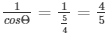
Therefore, Weget 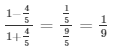
Q5) If tanΘ = 12/5, find the value of 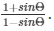
Solution:
cotΘ = 1/tanΘ = 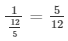
= cosecΘ = 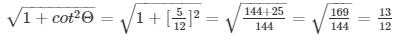
= sinΘ = 1/cosecΘ = 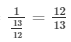
i.e. We get 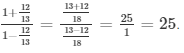
Q6) If cotΘ = 1/√3, find the value of 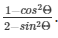
Solution:
cosecΘ = 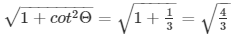
= cosecΘ = 2/√3
= sinΘ = 1/cosecΘ = 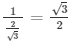
= and1/cotΘ = sinΘ/cosΘ = cosΘ = sinΘ × cotΘ = √3/2 × 1/√3 = 1/2
Therefore, on substituting we get
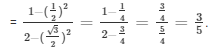
Q7) If cosecA = √2, find the value of 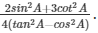
Solution:
We know that cotA =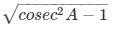
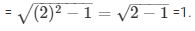
= tanA = 1/cotA = 1/1 = 1
= sinA = 1/cosecA = 1/√2
= sinA = 1/√2
cosA = 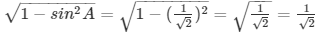
On substituting we get:
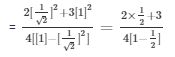
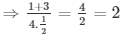
Q8) If cotΘ = √3, find the value of 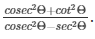
Solution:
cosecΘ = 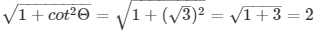
sinΘ = 1/cosecΘ = 1/2cotΘ = cosΘ/sinΘ .cosΘ = cotΘ.sinΘ
⇒ cosΘ = √3/2
= secΘ = 1/cosΘ = 2/√3
On substituting we get:
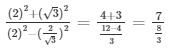
= 21/8
Q9) If 3cosΘ = 1, find the value of 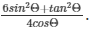
Solution:
cosΘ = 1/3,sinΘ = 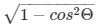
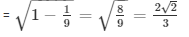
tanΘ = sinΘ/cosΘ = 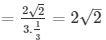
On substituting we get
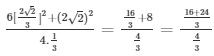
= 40/4 = 10
Q10) If √3tanΘ = sinΘ, find the value of sin2Θ−cos2Θ.
Solution:
√3.sinΘ/cosΘ = sinΘ
= cosΘ = √3/3⇒ 1/√3
= sinΘ = 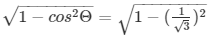
= sin2Θ−cos2Θ = 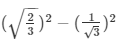
= 2/3−1/3 = 1/3
Q11) If cosecΘ = 13/12, find the value of 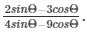
Solution:
sinΘ = 1/cosecΘ = 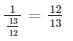
= cosΘ = 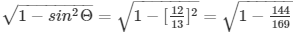
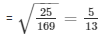
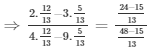
Q12) If sinΘ+cosΘ = √2cos(90°−Θ), find cotΘ.
Solution:
= sinΘ+cosΘ = √2sinΘ[cos(90−Θ) = sinΘ]
⇒ cosΘ = √2sinΘ − sinΘ ⇒ cosΘ = sinΘ(√2−1)
Divide both sides with sinΘ we get
= cosΘ/sinΘ = sinΘ/sinΘ(√2−1)
= cotΘ = √2−1.
Q-13. If 2sin2Θ – cos2Θ = 2, then find the value of Θ.
Solution.
2sin2Θ – cos2Θ = 2
⇒ 2sin2Θ−(1 – sin2Θ) = 2
⇒ 2sin2Θ – 1+sin2Θ = 2
⇒ 3sin2Θ = 3
⇒ sin2Θ = 1
⇒ sinΘ = 1
⇒ sinΘ = sin90°
⇒ Θ = 90°
Q-14. If √3tanΘ – 1 = 0, find the value of sin2Θ – cos2Θ.
Solution.
√3tanΘ – 1 = 0
⇒ √3tanΘ = 1
⇒ √3tanΘ = 1/√3
√3tanΘ = tan30°
Θ = 30°
Now,
sin2Θ – cos2Θ
= sin2(30°) – cos2(30°)
= (1/2)2 – (√3/2)2
= 1/4 – 3/4 = −2/4 = −1/2
|
5 videos|292 docs|59 tests
|
FAQs on Ex-6.2 Trigonometric Identities, Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. What are the basic trigonometric identities? |  |
| 2. How can I prove trigonometric identities? |  |
| 3. What is the importance of trigonometric identities? |  |
| 4. Can trigonometric identities be used in real-life applications? |  |
| 5. How can I remember all the trigonometric identities? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















