Ex-8.6 Quadratic Equations (Part - 1), Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Question 1: Determine the nature of the roots of the following quadratic equations.
Solution: (i) 2x2 -3x + 5 = 0
The given quadratic equation is in the form of ax2 + bx + c = 0
So a = 2, b = -3, c = 5
We know, determinant (D) = b2 – 4ac
= (-3)2 -4(2)(5)
= 9 – 40
= -31<0
Since D<0, the determinant of the equation is negative, so the expression does not having any real roots.
(ii) 2x2 -6x + 3 = 0
The given quadratic equation is in the form of ax2 + bx + c = 0
So a = 2, b = -6, c = 3
We know, determinant (D) = b2 – 4ac
= (-6)2 -4(2)(3)
= 36 – 24
= 12<0
Since D>0, the determinant of the equation is positive, so the expression does having any real and distinct roots.
(iii) For what value of k (4-k)x2 + (2k + 4)x + (8k + 1) = 0 is a perfect square.
The given equation is (4-k)x2 + (2k + 4)x + (8k + 1) = 0
Here, a = 4-k, b = 2k + 4, c = 8k + 1
The discriminate (D) = b2 – 4ac
= (2k + 4)2 – 4(4-k)(8k + 1)
= (4k2 + 16 + 16k) -4(32k + 4-8k2-k)
= 4(k2 + 8k2 + 4k-31k + 4-4)
= 4(9k2-27k)
D = 4(9k2-27k)
The given equation is a perfect square
D = 0
4(9k2-27k) = 0
9k2-27k = 0
Taking out common of of 3 from both sides and cross multiplying
= k2 -3k = 0
= K (k-3) = 0
Either k = 0
Or k = 3
The value of k is to be 0 or 3 in order to be a perfect square.
(iv) Find the least positive value of k for which the equation x2 + kx + 4 = 0 has real roots.
The given equation is x2 + kx + 4 = 0 has real roots
Here, a = 1, b = k, c = 4
The discriminate (D) = b2 – 4ac ≥0
= k2 – 16 ≥ 0
= k≤ 4 ,k≥-4
The least positive value of k = 4 for the given equation to have real roots.
(v) Find the value of k for which the given quadratic equation has real roots and distinct roots.
Kx2 + 2x + 1 = 0
The given equation is Kx2 + 2x + 1 = 0
Here, a = k, b = 2, c = 1
The discriminate (D) = b2 – 4ac ≥0
= 4 -4k ≥ 0 = 4k ≤4
K ≤ 1
The value of k ≤ 1 for which the quadratic equation is having real and equal roots.
(vi) Kx2 + 6x + 1 = 0
The given equation is Kx2 + 6x + 1 = 0
Here, a = k, b = 6, c = 1
The discriminate (D) = b2 – 4ac ≥0
= 36 -4k ≥ 0
= 4k ≤36
K ≤ 9
The value of k ≤ 9 for which the quadratic equation is having real and equal roots.
(vii) x2 –kx + 9 = 0
The given equation is X2 –kx + 9 = 0
Here, a = 1, b = -k, c = 9
Given that the equation is having real and distinct roots.
Hence, the discriminate (D) = b2 – 4ac ≥0
= k2 – 4(1)(9) ≥ 0
= k2 -36 ≥ 0
= k≥ -6 and k ≤6
The value of k lies between -6 and 6 respectively to have the real and distinct roots.
Question 2: Find the value of k.
(i) Kx2 + 4x + 1 = 0
The given equation Kx2 + 4x + 1 = 0 is in the form of ax2 + bx + c = 0 where a = k, b = 4, c = 1
Given that, the equation has real and equal roots
D = b2-4ac = 0
= 42-4(k)(1) = 0
= 16-4k = 0
= k = 4
The value of k is 4
(ii) kx2−2√5x + 4 = 0
The given equation kx2−2√5x + 4 = 0 is in the form of ax2 + bx + c = 0 where
a = k , b = −2√5 , c = 4
Given that, the equation has real and equal roots
D = b2-4ac = 0
= −2√52 −4 × k × 4 = 0
= 20-16k = 0
= k = 5/4
The value of k is k = 5/4
(iii) 3x2-5x + 2k = 0
The given equation 3x2-5x + 2k = 0 is in the form of ax2 + bx + c = 0 where a = 3, b = -5, c = 2k
Given that, the equation has real and equal roots
D = b2-4ac = 0
= (-5)2-4(3)(2k) = 0
= 25-24k = 0
K = k = 25/24
The value of the k is k = 25/24
(iv) 4x2 + kx + 9 = 0
The given equation 4x2 + kx + 9 = 0 is in the form of ax2 + bx + c = 0 where a = 4, b = k, c = 9
Given that, the equation has real and equal roots
D = b2-4ac = 0
= k2-4(4)(9) = 0
= k2 -144 = 0
= k = 12
The value of k is 12
(v) 2kx2-40x + 25 = 0
The given equation 2kx2-40x + 25 = 0 is in the form of ax2 + bx + c = 0 where a = 2k, b = -40, c = 25
Given that, the equation has real and equal roots
D = b2-4ac = 0
= (-40)2-4(2k)(25) = 0
= 1600-200k = 0
= k = 8
The value of k is 8
(vi) 9x2-24x + k = 0
The given equation 9x2-24x + k = 0 is in the form of ax2 + bx + c = 0 where a = 9, b = -24, c = k
Given that, the equation has real and equal roots
D = b2-4ac = 0
= (-24)2-4(9)(k) = 0
= 576-36k = 0 = k = 16
The value of k is 16
(vii) 4x2-3kx + 1 = 0
The given equation 4x2-3kx + 1 = 0 is in the form of ax2 + bx + c = 0 where a = 4, b = -3k, c = 1
Given that, the equation has real and equal roots D = b2-4ac = 0
= (-3k)2-4(4)(1) = 0
= 9k2-16 = 0
K = 4/3
The value of k is 4/3
(viii) x2-2(5 + 2k)x + 3(7 + 10k) = 0
The given equation X2-2(5 + 2k)x + 3(7 + 10k) = 0 is in the form of ax2 + bx + c = 0 where a = 1, b = + 2(52k) , c = 3(7 + 10k)
Given that, the nature of the roots of the equation are real and equal roots
D = b2-4ac = 0
= ( + 2(52k))2-4(1)( 3(7 + 10k)) = 0
= 4(5 + 2k)2 -12(7 + 10k) = 0
= 25 + 4k2 + 20k-21-30k = 0
= 4k2-10k + 4 = 0
Simplifying the above equation. We get,
= 2k2-5k + 2 = 0
= 2k2-4k-k + 2 = 0
= 2k(k-2)-1(k-2) = 0
= (k-2)(2k-1) = 0K = 2 and k = 1/2
The value of k can either be 2 or 1/2
(ix) (3k + 1)x2 + 2(k + 1)x + k = 0
The given equation (3k + 1)x2 + 2(k + 1)x + k = 0is in the form of ax2 + bx + c = 0 where a = 3k + 1, b = + 2(k + 1) , c = (k)
Given that, the nature of the roots of the equation are real and equal roots
D = b2-4ac = 0
= [2(k + 1)]2 -4(3k + 1)(k) = 0
= (k + 1)2-k(3k + 1) = 0
= -2k2 + k + 1 = 0
This equation can also be written as 2k2-k-1 = 0
The value of k can be obtained by
K = k = 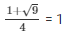
Or , k =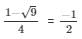
The value of k are 1 and −1/2 respectively.
(x) Kx2 + kx + 1 = -4x2-x
Bringing all the x components on one side we get ,
x2(4 + k) + x(k + 1) + 1 = 0
The given equation Kx2 + kx + 1 = -4x2-x is in the form of ax2 + bx + c = 0 where a = 4 + k,b = + k + 1 , c = 1
Given that, the nature of the roots of the equation are real and equal roots
D = b2-4ac = 0
= (k + 1)2-4(4 + k)(1) = 0
= k2-2k-10 = 0
The equation is also in the form ax2 + bx + c = 0
The value of k is obtained by a = 1 , b = -2 , c = -15

Putting the respective values in the above formula we will obtain the value of k
The value of k are 5 and -3 for different given quadratic equation.
(xi) (k + 1)x2 + 2(k + 3)x + k + 8 = 0
The given equation (k + 1) x2 + 2(k + 3)x + k + 8 = 0 is in the form of ax2 + bx + c = 0 where a = k + 1,b = 2(k + 3), c = k + 8
Given the nature of the roots of the equation are real and equal .
D = b2-4ac = 0
= [2(k + 30]2-4(k + 1)(k + 8) = 0
= 4(k + 3)2-4(k + 1)(k + 8) = 0
Taking out 4 as common from the LHS of the equation and dividing the same on the RHS
= (k + 3)2-(k + 1)(k + 8) = 0
= k2 + 9 + 6k – ( k2 + 9k + 18) = 0
Cancelling out the like terms on the LHS side
= 9 + 6k-9k-8 = 0
= -3k + 1 = 0
= 3k = 1
k = 1/3
The value of k of the given equation is k = 1/3
(xii) x2-2kx + 7k-12 = 0
The given equation is X2-2kx + 7k-12 = 0
The given equation is in the form of ax2 + bx + c = 0 where a = 1,b = -2k, c = 7k-12
Given the nature of the roots of the equation are real and equal .
D = b2-4ac = 0
= (2k)2-4(1)(7k-12) = 0
= 4k2-28k + 48 = 0
= k2-7k + 12 = 0
The value of k can be obtained by

Here a = 1 , b = -7k , c = 12
By calculating the value of k is 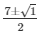 = 4 , 3
= 4 , 3
The value of k for the given equation is 4 and 3 respectively.
(xiii) (k + 1)x2-2(3k + 1)x + 8k + 1 = 0
The given equation is (k + 1)x2-2(3k + 1)x + 8k + 1 = 0
The given equation is in the form of ax2 + bx + c = 0 where a = k + 1,b = -2(k + 1), c = 8k + 1
Given the nature of the roots of the equation are real and equal.
D = b2-4ac = 0
= (-2(k + 1))2-4(k + 1)(8k + 1) = 0
= 4(3k + 1)2-4(k + 1)(8k + 1) = 0
Taking out 4 as common from the LHS of the equation and dividing the same on the RHS
= (3k + 1)2-(k + 1)(8k + 1) = 0
= 9k2 + 6k + 1 –( 8k2 + 9k + 1) = 0
= 9k2 + 6k + 1 – 8k2-9k-1 = 0
= k2-3k = 0
= k(k-3) = 0
Either k = 0
Or, k-3 = 0 = k = 3
The value of k for the given equation is 0 and 3 respectively.
(xiv) 5x2-4x + 2 + k(4x2-2x + 1) = 0
The given equation 5x2-4x + 2 + k(4x2-2x + 1) = 0 can be written as x2(5 + 4k)-x(4 + 2k) + 2-k = 0
The given equation is in the form of ax2 + bx + c = 0 where a = 5 + 4k, b = -(4 + 2k), c = 2-k
Given the nature of the roots of the equation are real and equal.
D = b2-4ac = 0
= [-(4 + 2k)]2-4(5 + 4k)(2-k) = 0
= 16 + 4k2 + 16- 4(10-5k + 8k-4k2] = 0
= 16 + 4k2 + 16- 40 + 20k-32k + 16k2 = 0
= 20k2 -4k-24 = 0
Taking out 4 as common from the LHS of the equation and dividing the same on the RHS
= 5k2-k-6 = 0
The value of k can be obtained by equation
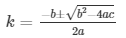
Here a = 5 , b = -1 , c = -6

k = 6/5 and−1
The value of k for the given equation are k = 6/5 and −1 respectively.
(xv) (4-k)x2 + (2k + 4)x + (8k + 1) = 0
The given equation is (4-k)x2 + (2k + 4)x + (8k + 1) = 0
The given equation is in the form of ax2 + bx + c = 0 where a = 4-k, b = (2k + 4), c = 8k + 1
Given the nature of the roots of the equation are real and equal.
D = b2-4ac = 0
= (2k + 4)2-4(4-k)(8k + 1) = 0
= 4k2 + 16k + 16 -4(-8k2 + 32k + 4-k) = 0
= 4k2 + 16k + 16 + 32k2-124k-16 = 0
Cancelling out the like and opposite terms. We get,
= 36k2-108k = 0
Taking out 4 as common from the LHS of the equation and dividing the same on the RHS
= 9k2-27k = 0
= 9k(k-3) = 0
Either 9k = 0
K = 0
Or, k-3 = 0
K = 3
The value of k for the given equation is 0 and 3 respectively.
(xvi) (2k + 1)x2 + 2(k + 3)x + (k + 5) = 0
The given equation is (2k + 1)x2 + 2(k + 3)x + (k + 5) = 0
The given equation is in the form of ax2 + bx + c = 0 where a = 2k + 1, b = 2(k + 3), c = k + 5
Given the nature of the roots of the equation are real and equal.
D = b2-4ac = 0
= [2(k + 3)]2-4(2k + 1)(k + 5) = 0
Taking out 4 as common from the LHS of the equation and dividing the same on the RHS
= [(k + 3)]2-(2k + 1)(k + 5) = 0
= K2 + 9 + 6k-(2k2 + 11k + 5) = 0
= -k2– 5k + 4 = 0
= k2 + 5k-4 = 0
The value of k can be obtained by k = 6/5 and−1 respectively.
Here a = 1 , b = 5 , c = -4
Now k = 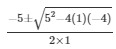
K = k = 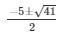
The value of k for the given equation is k = 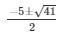
(xvii) 4x2-2(k + 1)x + (k + 4) = 0
The given equation is 4x2-2(k + 1)x + (k + 4) = 0
The given equation is in the form of ax2 + bx + c = 0 where a = 4, b = -2(k + 1), c = k + 4
Given the nature of the roots of the equation are real and equal.
D = b2-4ac = 0
= [-2(k + 1)]2-4(4)(k + 4) = 0
Taking out 4 as common from the LHS of the equation and dividing the same on the RHS
= (k + 1)2-4(k + 4) = 0
= k2 + 1 + 2k-4k-16 = 0
= k2-2k-15 = 0
The value of k can be obtained by k = 6/5 and−1 respectively.
Here a = 1 , b = -2 , c = -15
K = k =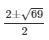
The value of k for the given equation is k = 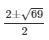
|
5 videos|292 docs|59 tests
|
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















