Probability Exercise 13.1(Part-2) | Extra Documents, Videos & Tests for Class 10 PDF Download
Q: 22. In a class, there are 18 girls and 16 boys. The class teacher wants to choose one pupil for class monitor. What she does, she writes the name of each pupil on a card and puts them into a basket and mixes thoroughly. A child is asked to pick one card from the basket. What is the probability that the name written on the card is:
(i) The name of a girl
(ii) The name of a boy?
Soln: Given: in a class there are 18 girls and 16 boys, the class teacher wants to choose one name. The class teacher writes all pupils’ name on a card and puts them in basket and mixes well thoroughly. A child picks one card
TO FIND: The probability that the name written on the card is
(i) The name of a girl
(ii) The name of a boy
Total number of students in the class 18 + 16 = 34
(i) The name of a girl are 18 hence favorable cases are 18
We know that PROBABILITY = 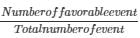
Hence probability of getting a name of girl on the card is equal to = 18/34 = 9/17
(ii) The name of a boy are 16 hence favorable cases are 16
We know that PROBABILITY = 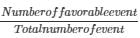
Hence probability of getting a name of boy on the card is equal to = 16/34 = 8/17
Q: 23. Why is tossing a coin considered to be a fair way of deciding which team should choose ends in a game of cricket?
Solution: No. of possible outcomes while tossing a coin = 2 {1 head & 1 tail}
Probability= 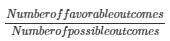
P( getting head) = 1/2
P( getting tail) = 1/2
Since, probability of two events are equal, these are called equally like events. Hence, tossing a coin is considered to be a fair way of deciding which team should choose ends in a game of cricket.
Q: 24. What is the probability that a number selected at random from the number 1,2,2,3,3,3, 4, 4, 4, 4 will be their average?
Solution:
Given no’s are 1, 2, 2, 3, 3, 3, 4, 4, 4, 4
Total no. of possible outcomes =10
Average of the no’s = 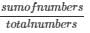
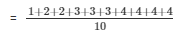
= 30/10
= 3
E = event of getting 3
No. of favorable outcomes = 3 {3, 3, 3}
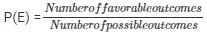
P(E) = 3/10
Q: 25. There are 30 cards, of same size, in a bag on which numbers 1 to 30 are written. One card is taken out of the bag at random. Find the probability that the number on the selected card is not divisible by 3.
Solution:
Total no. of possible outcomes – 30 { 1, 2, 3, … 30)
E = event of getting number divisible by 3
Number of favorable outcomes = 10 {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}
Probability, P(E) = 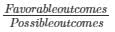
P(E) = 10/30
= 1/3
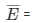 event of getting number not divisible by 3
event of getting number not divisible by 3
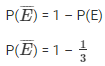
= 2/3
Q: 26. A bag contains 5 red, 8 white and 7 black balls. A ball is drawn at random from the bag. Find the probability that the drawn ball is
(i) red or white
(ii) not black
(ii) neither white nor black.
Solution:
Total number of possible outcomes = 20 (5 red, 8 white & 7 black}
(i) E = event of drawing red or white ball
No. of favorable outcomes = 13 {5 red, 8 white}
Probability, P(E) = 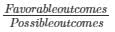
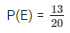
(ii) Let E = event of getting black ball
No. of favorable outcomes =7 {7 black balls}
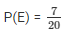
 event of not getting black ball
event of not getting black ball
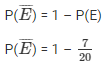
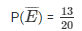
(iii) Let E = event of getting neither white nor black ball
No. of favorable outcomes = 20 – 8 – 7
= 5 {total balls – no. of white balls – no. of black balls}
P(E) = 5/20
P(E) = 1/4
Q: 27. Find the probability that a number selected from the number 1 to 25 is not a prime number when each of the given numbers is equally likely to be selected.
Solution:
Total no. of possible outcomes = 25 {1, 2, 3…. 25}
E = event of getting a prime no.
No. of favorable outcomes = 9 {2, 3, 5, 7, 11, 13, 17, 19, 23}

P(E) = 9/25
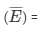 event of not getting a prime
event of not getting a prime
P  1— P(E)
1— P(E)
P 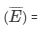 1 - 9/5925
1 - 9/5925
P 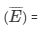 16/25
16/25
Q: 28. A bag contains 8 red, 6 white and 4 black balls. A ball is drawn at random from the bag. Find the probability that the drawn ball is
(i) Red or white
(ii) Not black
(iii) Neither white nor black
Solution:
Total no. of possible outcomes = 8 + 6 + 4 =18 {8 red, 6 white, 4 black)
(i) E = event of getting red or white ball
No. of favorable outcomes = 14 {8 red balls, 6 white balls}
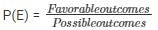
P(E) = 14/18
P(E) = 7/9
(ii) E = event of getting a black ball
Number of favorable outcomes = 4 {4 black balls}
P(E) = 4/18
P(E) = 2/9
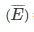 = event of not getting a black ball
= event of not getting a black ball
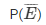 =1 – P(E)
=1 – P(E)
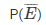 = 1- 2/9
= 1- 2/9
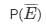 = 7/9
= 7/9
(iii) E = event of getting neither white nor black
No. of favorable outcomes = 18 – 6 – 4
= 8(Total balls – no. of white balls – no. of black balls)
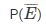 = 8/18
= 8/18
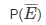 = 4/9
= 4/9
Q: 29. Find the probability that a number selected at random from the numbers 1, 2, 3…. 35 is a:
(i) Prime number
(ii) Multiple of 7
(iii) Multiple of 3 or 5
Solution:
Total no. of possible outcomes = 35 {1, 2, 3….. 35}
(i) E = event of getting a prime no.
No. of favorable outcomes =11 {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31)

P(E) = 11/35
(ii) E = event of getting no. which is multiple of 7
No. of favorable outcomes = 5 {7, 14, 21, 28, 35}
P(E) = 5/35
P(E)= 1/7
(iii) E = event of getting no which is multiple of 3 or 5
No. of favorable outcomes = 16 {3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 5, 10, 20, 25, 35}
P(E) = 16/35
Q: 30. From a pack of 52 playing cards Jacks, queens, kings and aces of red color are removed. From the remaining, a card is drawn at random. Find the probability that the card drawn is
(i) A black queen
(ii) A red card
(iii) A black jack
(iv) a picture card (Jacks. queens and kings are picture cards)
Solution:
Total no. of cards = 52
All jacks, queens & kings, aces of red color are removed.
Total no. of possible outcomes = 52 – 2 – 2 – 2 – 2 = 44 {remaining cards}
(i) E = event of getting a black queen
No. of favorable outcomes = 2 {queen of spade & club}

P(E) = 1/22
(ii) E = event of getting a red card
No. of favorable outcomes = 26-8
= 18 (total red cards jacks – queens, kings, aces of red color)
P(E)= 18/44
P(E)= 9/22
(iii) E = event of getting a black jack
No. of favorable outcomes = 2 {jack of club & spade}
P(E)= 2/44
P(E)= 1/22
(iv) E = event of getting a picture card
No. of favorable outcomes = 6 {2 jacks, 2 kings & 2 queens of black color}
P(E) = 6/44
P(E) = 3/22
Q: 31. A bag contains lemon flavored candies only. Malini takes out one candy without looking into the bag. What is the probability that she takes out :
(i) an orange flavored candy
(ii) a lemon flavored candy
Solution:
(i) The bag contains lemon flavored candies only. So, the event that Malini will take out an orange flavored candy is an impossible event.
Since, probability of impossible event is 0, P(an orange flavored candy) = 0
(ii) The bag contains lemon flavored candies only. So, the event that Malini will take out a lemon flavored candy is sure event. Since probability of sure event is 1.
P(a lemon flavored candy) = 1
Q: 32. It is given that in a group of 3 students, the probability of 2 students not having the same birthday is 0.992. What is the probability that the 2 students have the same birthday?
Solution:
Let E = event of 2 students having same birthday
P(E) is given as 0.992
Let, 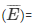 event of 2 students not having same birthday.
event of 2 students not having same birthday.
We know that,
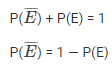
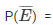 1 – 0.992 = 0.008
1 – 0.992 = 0.008
Q: 33. A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is
(i) red
(ii) not red
Solution:
Total no. of possible outcomes = 8 {3 red, 5 black}
(i) E = event of getting red ball.
No. of favorable outcomes = 3 {3 red}
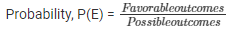
P(E) = 3/8
(ii) E = event of getting no red ball.
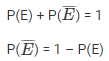
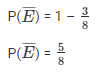
Q: 34. A box contains 5 red marbles, 8 white marbles and 4 green marbles. One marble is taken out of the box at random. What is the probability that the marble taken out will be:
(i) red
(ii) not green
Solution:
Total no. of possible outcomes = 17 { 5 red, 8 white, 4 green}
(i) E = event of getting a red marble
Number of favorable outcomes = 5 {5 red marbles}

(ii) E= event of getting a green marble
Number of favorable outcomes = 4 {4 green marbles}
P(E) = 4/17
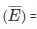 event of getting not a green marble
event of getting not a green marble

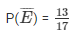
Q: 35. A lot consists of 144 ball pens of which 20 are defective and others good. Nuri will buy a pen if it is good, but will not buy if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that
(i)She will buy it
(ii) She will not buy it
Sol:
No. of good pens =144 —20 = 24
No. of detective pens = 20
Total no. of possible outcomes =144 (total no. of pens)
(i) E = event of buying pen which is good.
No. of favorable outcomes =124 (124 good pens)
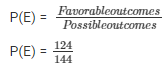
P(E) = 31/36
(ii) E = event of not buying a pen which is bad
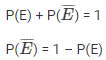
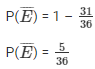
Q: 36. 12 defective pens are accidently mixed with 132 good ones. It is not possible to just look at pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen taken out is good one.
Solution:
No. of good pens =132
No. of defective pens = 12
Total no. of possible outcomes = 132 + 12 {total no of pens}=144
E = event of getting a good pen.
No. of favorable outcomes =132 {132 good pens}

P(E) = 132/144
P(E) = 11/12
Q: 37. Five cards— the ten, jack, queen, king and ace of diamonds, are well shuffled with their face downwards. One card is then picked up at random.
(i) What is the probability that the card is the queen?
(ii) If the queen is drawn and put aside, what is the probability that the second card picked up is
- a) an ace?
b)a queen?
Solution:
Total no. of possible outcomes = 5 {5 cards}
(i) E = event of getting a queen.
No. of favorable outcomes = 1 {1 queen}
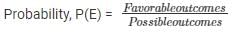
P(E) = 1/5
(ii) If queen is drawn & put aside.
Total no. of remaining cards = 4
(a) E = events of getting a queen.
No. of favorable outcomes = 3
Total no. of possible outcomes = 4 {4 remaining cards}
P(E) = 3/4
(b) E = event of getting a good pen.
No. of favorable outcomes = 0 {there is no queen}
P(E) = 0
Therefore, E is known as impossible event.
Q: 38. Harpreet tosses two different coins simultaneously (say, one is of Re 1 and other of Rs 2). What is the probability that he gets at least one head?
Solution:
Total no. of possible outcomes = 4 which are{HT, HH, TT, TH}
E = event of getting at least one head
No. of favorable outcomes = 3 {HT, HH, TH}
Probability, P(E) = 
P(E) = 3/4
Q: 39. Cards marked with numbers 13, 14, 15…. 60 are placed in a box and mixed thoroughly. One card is drawn at random from the box. Find the probability that number on the card drawn is:
(i) divisible by 5
(ii) a number is a perfect square
Solution:
Total no. of possible outcomes = 48{13, 14, 15, ….,60)
(i) E = event of getting no divisible by 5
No. of favorable outcomes =10{15, 20, 25, 30, 35, 40, 45, 50, 55, 60}
Probability, P(E) = 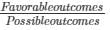
P(E) = 10/48
P(E) = 5/24
(ii) E = event of getting a perfect square.
No. of favorable outcomes = 4 {16, 25, 36, 49)
P(E) = 4/68
P(E) = 1/16
Q: 40. A bag contains tickets numbered 11, 12……. 30. A ticket is taken out from the bag at random. Find the probability that the number on the drawn ticket
(i) is a multiple of 7
(ii) is greater than 15 and a multiple of 5.
Solution:
Total no. of possible outcomes = 20 {11, 12, 13…… 30}
(i) E = event of getting no. which is multiple of 7
No. of favorable outcomes = 3 {14, 21, 28}
Probability, P(E) = 
P(E) = 3/20
(ii) E = event of getting no. greater than 15 & multiple of 5
No. of favorable outcomes = 3 {20, 25, 30}
P(E) = 3/20
Q: 41. Fill in the blanks:
(i) Probability of a sure event is …….
(ii)Probability of an impossible event is ……..
(iii)The probability of an event (other than sure and impossible event) lies between ……
(iv)Every elementary event associated to a random experiment has ………. probability.
(v) Probability of an event A + Probability of event ‘not A’ = ……………..
(vi) Sum of the probabilities of each outcome in an experiment is ………….
Solution:
(i) 1, P(sure event) =1
(ii) 0, P (impossible event) = 0
(iii) 0 & 1,0 < P(E) <1
(iv)Equal
(v) 1, P(E) + 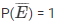
(vi)1
Q: 42. Examine each of the following statements and comment:
(i) If two coins are tossed at the same time. There are 3 possible outcomes—two heads, two tails, or one of each. Therefore, for each outcome, the probability of occurrence is 1/3 .
(ii) If a die is thrown once, there are two possible outcomes – an odd number or an even number. Therefore, the probability of obtaining an odd number is 1/2 and the probability of obtaining an even number is 1/2 .
Solution:
(i) Given statement is incorrect. If 2 coins are tossed at the same time.
Total no. of possible outcomes = 4 {HH, HT, TH, TT}
P(HH)= P(HT) = P(TH) = P(TT) = 1/4
Outcomes can be classified as (2H, 2T, 1H & 1T)

P(1H & 1T)= 1/2
Events are not equally likely because the event ‘one head & one tail’ is twice as likely to occur as remaining two.
(ii) This statement is true.
When a die is thrown; total no. of possible outcomes = 6 {1, 2, 3, 4, 5, 6}
These outcomes can be taken as even number & odd number.
P(even no.) = P(2, 4, 6) = 3/6 = 1/2
P(odd no.) = P(1, 3,5) = 3/6 = 1/2
Therefore, two outcomes are equally likely
|
5 videos|292 docs|59 tests
|
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















