Ex-8.7 Quadratic Equations (Part - 1), Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Question 1: Find the consecutive numbers whose squares have the same sum of 85.
Solution:
Let the two consecutive two natural numbers be (x) and ( x + 1) respectively.
Given,
That the sum of their squares is 85.
Then, by hypothesis, we get,
= x2 + (x + 1)2 = 85
= x2 + x2 + 2x + 1 = 85
= 2x2 + 2x + 1 - 85 = 0
= 2x2 + 2x + - 84 = 0
= 2(x2 + x + - 42) = 0
Now applying factorization method, we get,
= x2 + 7x - 6x - 42 = 0
= x(x + 7) - 6(x + 7) = 0
= (x - 6)(x + 7) = 0
Either,
x - 6 = 0 therefore , x = 6
x + 7 = 0 therefore x = - 7
Hence the consecutive numbers whose sum of squares is 85 are 6 and - 7 respectively.
Question 2: Divide 29 into two parts so that the sum of the squares of the parts is 425.
Solution:
Let the two parts be (x) and (29 - x) respectively.
According to the question, the sum of the two parts is 425.
Then by hypothesis,
= x2 + (29 - x)2 = 425
= x2 + x2 + 841 + - 58x = 425
= 2x2 - 58x + 841 - 425 = 0
= 2x2 - 58x + 416 = 0
= x2 - 29x + 208 = 0
Now, applying the factorization method
= x2 - 13x - 16x + 208 = 0
= x(x - 13) - 16(x - 13) = 0
= (x - 13)(x - 16) = 0
Either x - 13 = 0 therefore x = 13
Or, x - 16 = 0 therefore x = 16
The two parts whose sum of the squares is 425 are 13 and 16 respectively.
Question 3: Two squares have sides x cm and (x + 4) cm. The sum of their areas is 656 cm2.find the sides of the squares.
Solution:
Given,
The sum of the sides of the squares are = x cm and (x + 4) cm respectively.
The sum of the areas = 656 cm2
We know that,
Area of the square = side * side
Area of the square = x(x + 4) cm2
Given that the sum of the areas is 656 cm2
Hence by hypothesis,
= x(x + 4) + x(x + 4) = 656
= 2x(x + 4) = 656
= x2 + 4x = 328
Now by applying factorization method,
= x2 + 20x - 16x - 328 = 0
= x(x + 20) - 16(x + 20) = 0
= (x + 20)(x16) = 0
Either x + 20 = 0 therefore x = - 20
Or, x - 16 = 0 therefore x = 16
No negative value is considered as the value of the side of the square can never be negative.
Therefore, the side of the square is 16.
Therefore, x + 4 = 16 + 4 = 20 cm
Hence, the side of the square is 20cm.
Question 4: The sum of two numbers is 48 and their product is 432. Find the numbers.
Solution:
Given the sum of two numbers is 48.
Let the two numbers be x and 48 - x also the sum of their product is 432.
According to the question
= x(48 - x) = 432
= 48x - x2 = 432
= x2 - 48x + 432 = 0
= x2 - 36x - 12x + 432 = 0
= x(x - 36) - 12(x - 36) = 0
= (x - 36)(x - 12) = 0
Either x - 36 = 0 therefore x = 36
Or, x - 12 = 0 therefore x = 12
The two numbers are 12 and 36 respectively.
Question 5: If an integer is added to its square, the sum is 90. Find the integer with the help of quadratic equation.
Solution:
Let the integer be x
Given that if an integer is added to its square , the sum is 90
= x + x2 = 90
= x2 + x - 90 = 0
= x2 + 10x - 9x - 90 = 0
= x(x + 10) - 9(x + 10) = 0
= (x + 10)(x - 9) = 0
Either x + 10 = 0
Therefore x = - 10
Or, x - 9 = 0
Therefore x = 9
The values of the integer are 9 and - 10 respectively.
Question 6: Find the whole numbers which when decreased by 20 is equal to69 times the reciprocal of the numbers.
Solution:
Let the whole number be x cm
As it is decreased by 20 = (x - 20) = 69/x
x - 20 = 69/x
x(x - 20) = 69
x2 - 20x - 69 = 0
Now by applying factorization method ,
x2 - 23x + 3x - 69 = 0
x(x - 23) + 3(x - 23) = 0
(x - 23)(x + 3) = 0
Either, x = 23
Or, x = - 3
As the whole numbers are always positive x = - 3 is not considered.
The whole number is 23.
Question 7: Find the consecutive natural numbers whose product is 20
Solution:
Let the two consecutive natural number be x and x + 1 respectively.
Given that the product of natural numbers is 20
= x(x + 1) = 20
= x2 + x - 20 = 0
= x2 + 5x - 4x - 20 = 0
= x(x + 5) - 4(x + 5) = 0
= (x + 5)(x - 4) = 0
Either x + 5 = 0
Therefore x = - 5
Considering the positive value of x.
Or, x - 4 = 0
Therefore x = 4
The two consecutive natural numbers are 4 and 5 respectively.
Question 8: The sum of the squares of two consecutive odd positive integers is 394. Find the two numbers?
Solution:
Let the consecutive odd positive integer are 2x - 1 and 2x + 1 respectively.
Given, that the sum of the squares is 394.
According to the question,
(2x - 1)2 + (2x + 1)2 = 394
4x2 + 1 - 4x + 4x2 + 1 + 4x = 394
Now cancelling out the equal and opposite terms ,
8x2 + 2 = 394
8x2 = 392
X2 = 49
X = 7 and - 7
Since the value of the edge of the square cannot be negative so considering only the positive value.
That is 7
Now, 2x - 1 = 14 - 1 = 13
2x + 1 = 14 + 1 = 15
The consecutive odd positive numbers are 13 and 15 respectively.
Question 9: The sum of two numbers is 8 and 15 times the sum of the reciprocal is also 8 . Find the numbers.
Solution:
Let the numbers be x and 8 - x respectively.
Given that the sum of the numbers is 8 and 15 times the sum of their reciprocals.
According to the question,
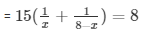
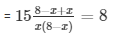

= 120 = 8(8x - x2)
= 120 = 64x - 8x2
= 8x2 - 64x + 120 = 0
= 8(x2 - 8x + 15) = 0
= x2 - 8x + 15 = 0
= x2 - 5x - 3x + 15 = 0
= x(x - 5) - 3(x - 5) = 0
= (x - 5)(x - 3) = 0
Either x - 5 = 0 therefore x = 5
Or, x - 3 = 0 therefore x = 3
The two numbers are 5 and 3 respectively.
Question 10: The sum of a number and its positive square root is 625. Find the numbers.
Solution:
Let the number be x
By the hypothesis, we have
x + √ x = 6/25
Let us assume that x = y2 , we get
y + y2 = 6/25
= 25y2 + 25y - 6 = 0
The value of y can be determined by:
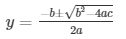
Where a = 25, b = 25 , c = - 6
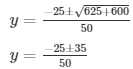

The number x is 1/25
Question 11: There are three consecutive integers such that the square of the first increased by the product of the other two integers gives 154. What are the integers?
Solution:
Let the three consecutive numbers be x, x + 1, x + 2 respectively.
X2 + (x + 1)(x + 2) = 154
= x2 + x2 + 3x + 2 = 154
= 3x2 + 3x - 152 = 0
The value of x can be obtained by the formula
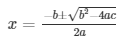
Here a = 3 , b = 3 , c = 152
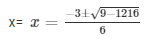
x = 8andx = −19/2
Considering the value of x
If x = 8
x + 1 = 9
x + 2 = 10
The three consecutive numbers are 8 , 9 , 10 respectively.
Question 12: The product of two successive integral multiples of 5 is 300. Determine the multiples.
Solution:
Given that the product of two successive integral multiples of 5 is 300
Let the integers be 5x and 5(x + 1)
According to the question,
5x[5(x + 1)] = 300
= 25x(x + 1) = 300
= x2 + x = 12
= x2 + x - 12 = 0
= x2 + 4x - 3x - 12 = 0
= x(x + 4) - 3(x + 4) = 0
= (x + 4)(x - 3) = 0
Either x + 4 = 0
Therefore x = - 4
Or, x - 3 = 0
Therefore x = 3
x = - 4
5x = - 20
5(x + 1) = - 15
x = 3
5x = 15
5(x + 1) = 20
The two successive integral multiples are 15,20 and - 15 and - 20 respectively.
Question 13: The sum of the squares of two numbers is 233 and one of the numbers is 3 less than the other number. Find the numbers.
Solution:
Let the number is x
Then the other number is 2x - 3
According to the question:
x2 + (2x - 3)2 = 233
= x2 + 4x2 + 9 - 12x = 233
= 5x2 - 12x - 224 = 0
The value of x can be obtained by x = 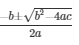
Here a = 5 , b = - 12 , c = - 224
x = x = 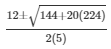
x = 8 and x = −28/5
Considering the value of x = 8
2x - 3 = 15
The two numbers are 8 and 15 respectively.
Question 14: The difference of two number is 4 . If the difference of the reciprocal is 4/21 . find the numbers.
Solution:
Lethe two numbers be x and x - 4 respectively.
Given, that the difference of two numbers is 4 .
By the given hypothesis we have,
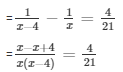
= 84 = 4x(x - 4)
= x2 - 4x - 21 = 0
Applying factorization theorem,
= x2 - 7x + 3x - 21 = 0
= (x - 7)(x + 3) = 0
Either x - 7 = 0 therefore x = 7
Or, x + 3 = 0 therefore x = - 3
Hence the required numbers are - 3 and 7 respectively.
Question 15: Let us find two natural numbers which differ by 3 and whose squares have the sum 117.
Solution:
Let the numbers be x and x - 3
According to the question
x2 + (x - 3)2 = 117
= x2 + x2 + 9 - 6x - 117 = 0
= 2x2 - 6x - 108 = 0
= x2 - 3x - 54 = 0
= x2 - 9x + 6x - 54 = 0
= x(x - 9) + 6(x - 9) = 0
= (x - 9)(x + 6) = 0
Either x - 9 = 0 therefore x = 9
Or ,x + 6 = 0 therefore x = - 6
Considering the positive value of x that is 9
x = 9
x - 3 = 6
The two numbers are 6 and 9 respectively.
Question 16: The sum of the squares of these consecutive natural numbers is 149. Find the numbers.
Solution:
Let the numbers be x , x + 1, and x + 2 respectively.
According to given hypothesis
X2 + (x + 1)2 + (x + 2)2 = 149
X2 + X2 + X2 + 1 + 2x + 4 + 4x = 149
3x2 + 6x - 144 = 0
X2 + 2x - 48 = 0
Now applying factorization method,
X2 + 8x - 6x - 48 = 0
X(x + 8) - 6(x + 8) = 0
(x + 8)(x - 6) = 0
Either x + 8 = 0 therefore x = - 8
Or, x - 6 = 0 therefore x = 6
Considering only the positive value of x that is 6 and discarding the negative value.
x = 6
x + 1 = 7
x + 2 = 8The three consecutive numbers are 6 , 7 , and 8 respectively.
|
5 videos|292 docs|59 tests
|
FAQs on Ex-8.7 Quadratic Equations (Part - 1), Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. What are quadratic equations? |  |
| 2. How do you solve quadratic equations? |  |
| 3. What is the quadratic formula? |  |
| 4. How many solutions can a quadratic equation have? |  |
| 5. What are the applications of quadratic equations in real life? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|











