Ex-8.7 Quadratic Equations (Part - 2), Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download

Question 17: Sum of two numbers is 16. The sum of their reciprocal is 13.find the numbers.

Solution:

Given that the sum of the two natural numbers is 16

Let the two natural numbers be x and 16 - x respectively

According to the question

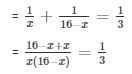
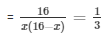
= 16x - x²  = 48

= - 16x + x² + 48 = 0

= + x² - 16x + 48 = 0

= + x² - 12x - 4x + 48 = 0

= x(x - 12) - 4(x - 12) = 0

= (x - 12)(x - 4) = 0

Either x - 12 = 0 therefore x = 12

Or , x - 4 = 0 therefore x = 4

The two numbers are 4 and 12 respectively.

Question 18: Determine the two consecutive multiples of 3 whose product is 270

Solution:

Let the consecutive multiples of 3 are 3xand 3x + 3

According to the question

3x(3x + 3) = 270

= x(3x + 3) = 90

= 3x² + 3x = 90

= 3x² + 3x - 90 = 0

= x² + x - 30 = 0

= x² + 6x - 5x - 30 = 0

= x(x + 6) - 5(x + 6) = 0

= (x + 6)(x - 5) = 0

Either x + 6 = 0 therefore x = - 6

Or , x - 5 = 0 therefore x = 5

Considering the positive value of x

x = 5

3x = 15

3x + 3 = 18

The two consecutive multiples of 3 are 15 and 18 respectively.

Question 19: The sum of a number and its reciprocal is 17/4 . find the numbers.

Solution:

Lethe number be x

According to the question

= 4(x² + 1) = 17x

= 4x² + 4 - 17x = 0

= 4x² + 4 - 16x - x = 0

= 4x(x - 4) - 1(x - 4) = 0

= (4x - 1)(x - 4) = 0

Either x - 4 = 0 therefore x = 4

Or, 4x - 1 = 0 therefore x = 1/4

The value of x is 4

Question 20: A two digit is such that the products of its digits is 8when 18 is subtracted from the number, the digits interchange their places. Find the number?

Solution:

Let the digits be x and x - 2 respectively.

The product of the digits is 8

According to the question

x(x - 2) = 8

= x² - 2x - 8 = 0

= x² - 4x + 2x - 8 = 0

= x(x - 4) + 2(x - 4) = 0

Either x - 4 = 0 therefore x = 4

Or , x + 2 = 0 therefore x = - 2

Considering the positive value of x = 4

x - 2 = 2

The two digit number is 42.

Question 21: A two digit number is such that the product of the digits is 12, when 36 is added to the number, the digits interchange their places .find the number.

Solution:

Let the tens digit be x

Then, the unit digit =  12/x

Therefore the number =  10x + 12/x

And, the number obtained by interchanging the digits =  x + 120/x

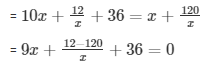
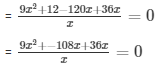
= 9(x² + 4x - 12) = 0

= (x² + 4x - 12) = 0

= x² + 6x - 2x - 12 = 0

= x(x + 6) - 2(x + 6) = 0

= (x - 2)(x + 6) = 0

Either x - 2 = 0 therefore x = 2

Or, x + 6 = 0 therefore x = - 6

Since a digit can never be negative. So x = 2

The number is 26.

Question 22: A two digit number is such that the product of the digits is 16 when 54 is subtracted from the number, the digits are interchanged. Find the number.

Solution:

Let the two digits be:

Tens digit be x

Units digit be 16/x

Numbers =  10x + 16/x ……………………….(i)

Number obtained by interchanging =  10(10x + 16/x)

10x + 16/x – 10(10x + 16/x)  = 54

= 10x² + 16 - 160 + x²  = 54

= 9x² - 54x - 144 = 0

= x² - 6x - 16 = 0

= x² - 8x + 2x - 16 = 0

= x(x - 8) + 2(x - 8) = 0

= (x - 8)(x + 2) = 0

Either x - 8 = 0 therefore x = 8

Or, x + 2 = 0 therefore x = - 2

A digit can never be negative so x = 8

Hence by putting the value of x in the above equation (i) the number is 82.

Question 23: Two numbers differ by 3 and their product is 504. Find the numbers.

Solution:

Let the numbers be x and x - 3 respectively.

According to the question

= x(x - 3) = 504

= x² - 3x - 504 = 0

= x² - 24x + 21x - 504 = 0

= x(x - 24) + 21 (x - 24) = 0

= (x - 24)(x + 21) = 0

Either x - 24 = 0 therefore x = 24

Or , x + 21 = 0 , therefore x = - 21

x = 24 and x = - 21

x - 3 = 21 and x - 3 = - 24

The two numbers are 21 a nd 24 and - 21 and - 24 respectively.

Question 24: Two numbers differ by 4 and their product is 192. Find the numbers.

Solution:

Let the two numbers be x and x - 4 respectively

Given that the product of the numbers is 192

According to the question

= x(x - 4) = 192

= x² - 4x - 192 = 0

=    x² - 16x + 12x - 192 = 0

= x(x - 16) + 12(x - 16) = 0

= (x - 16) (x + 12) = 0

Either x - 16 = 0 therefore x = 16

Or, x + 12 = 0 therefore x = - 12

Considering only the positive value of x

x = 16S

x - 4 = 12

The two numbers are 12 and 16 respectively.

Question 25: A two digit number is 4 times the sum of its digits and twice the product of its digits. Find the numbers.

Solution:

Let the digit in the tens and the units place be x and y respectively.

Then it is represented by 10x + y

According to the question,

10x + y = 4(sum of the digits) and 2xy

10x + y = 4(x + y) and 10x + y = 2xy

10x + y = 4x + 4y and 10x + y = 2xy

6x - 3y = 0 and 10x + y - 2xy = 0

y = 2x and 10x + 2x - 2x(2x) = 0

12x = 4x²

4x(x - 3) = 0

Either 4x = 0 therefore x = 0

Or, x - 3 = 0 therefore x = 3

We have y = 2x

When x = 3 , y = 6

Question 26: The sum of the squares of two positive integers is 208. If the square of the large number is 18 times the smaller. Find the numbers.

Solution:

Let the smaller number be x

Then, square of the large number be = 18x

Also, square of the smaller number be = x²

It is given that the sum of the square of the integer is 208.

Therefore,

= x²  + 18x = 208

= x² + 18x - 208 = 0

Applying factorization theorem,

= x²  + 26x - 8x - 208 = 0

= x(x + 26) - 8(x + 26) = 0

= (x + 26)(x - 8) = 0

Either x + 26 = 0 therefore x = - 26

Or, x - 8 = 0 therefore x = 8

Considering the positive number, therefore x = 8.

Square of the largest number = 18x = 18*8 = 144

Largest number = 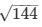 = 12

Hence the numbers are 8 and 12 respectively.

Question 27: The sum of two numbers is 18. The sum of their reciprocal is 1/4 .find the numbers.

Solution:

Let the numbers be x and (18 - x) respectively.

According to the given hypothesis,

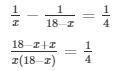
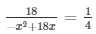
= 72 = 18x - x²

= x² - 18x + 72 = 0

Applying factorization theorem, we get,

= x²  - 6x - 12x + 72 = 0

= x(x - 6) - 12(x - 6) = 0

= (x - 6)(x - 12) = 0

Either, x = 6

Or, x = 12

The two numbers are 6 and 12 respectively.

Question 28: The sum of two numbers a and b is 15 and the sum of their reciprocals 1/a and 1/b is 3/10. Find the numbers  a and b.

Solution:

Let us assume a number x such that

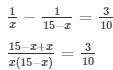
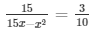
= 3x² - 45x + 150 = 0

= x²  - 15 x + 50 = 0

Applying factorization theorem,

= x²– 10x - 5x + 50 = 0

= x(x - 10) - 5(x - 10) = 0

= (x - 10)(x - 5) = 0

Either, x - 10 = 0 therefore x = 10

Or, x - 5 = 0 therefore x = 5

Case (i)

If x = a , a = 5 and b = 15 - x , b = 10

Case (ii)

If x = 15 - a = 15 - 10 = 5 ,

x = a = 10 , b = 15 - 10 = 5

Hence when a = 5 , b = 10

a = 10 , b = 5

 Question 29: The sum of two numbers is 9. The sum of their reciprocal is 1/2.find the numbers.

Solution:

Given that the sum of the two numbers is 9

Let the two number be x and 9 - x respectively

According to the question

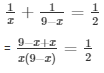
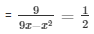
= 9x - x² = 18

= x² - 9x + 18 = 0

= x² - 6x - 3x + 18 = 0

= x(x - 6) - 3(x - 6) = 0

= (x - 6)(x - 3) = 0

Either x - 6 = 0 therefore x = 6

Or x - 3 = 0 therefore x = 3

The two numbers are 3 and 6 respectively

Question 30: Three consecutive positive integers are such that the sum of the squares of the first and the product of the other two is 46. Find the integers.

Solution:

Let the consecutive positive integers be x , x + 1, x + 2 respectively

According to the question

X² + (x + 1)(x + 2) = 46

= x² + x² + 3x + 2 = 46

= 2 x² + 3x + 2 = 46

= 2 x² + 3x + 2 - 46 = 0

= 2 x² - 8x + 11x + - 44 = 0

= 2x(x - 4) + 11(x - 4) = 0

= (x - 4)(2x + 11) = 0

Either x - 4 = 0 therefore x = 4

Or, 2x + 11 = 0 therefore  x = −11/2

Considering the positive value of x that is x = 4

The three consecutive numbers are 4 , 5  and 6 respectively

Question 31: The difference of squares of two numbers is 88. If the large number is 5 less than the twice of the smaller, then find the two numbers

Solution:

Let the smaller number be x and larger number is 2x - 5

It is given that the difference of the squares of the number is 88

According to the question

(2x - 5)² - x² = 88

= 4x² + 25 - 20x - x²  = 88

= 3x² - 20x - 63 = 0

= 3x² - 27x + 7x - 63 = 0

= 3x(x - 9) + 7(x - 9) = 0

= (x - 9)(3x + 7) = 0

Either x - 9 = 0 therefore x = 9

Or, 3x + 7 = 0 therefore x = −7/3

Since a digit can never be negative so x = 9

Hence the number is 2x - 5 = 13

The required numbers are 9 and 13 respectively

Question 32: The difference of squares of two numbers is180. The square of the smaller number is 8 times the larger number. Find the two numbers

Solution:

Let the number be x

According to the question

X² - 8x = 180

X² - 8x - 180 = 0

= X² + 10x - 18x - 180 = 0

= x(x + 10) - 18(x - 10) = 0

= (x - 18)(x + 10) = 0

Either x - 18 = 0 therefore x = 18

Or, x + 10 = 0 therefore x = - 10

Case (i)

X = 18

8x = 144

Larger number = 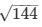 = 12

Case (ii)

X = - 10

Square of the larger number 8x = - 80

Here in this case no perfect square exist

Hence the numbers are 18 and 12 respectively .