Ex-8.7 Quadratic Equations (Part - 2), Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Question 17: Sum of two numbers is 16. The sum of their reciprocal is 13.find the numbers.
Solution:
Given that the sum of the two natural numbers is 16
Let the two natural numbers be x and 16 - x respectively
According to the question
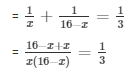
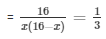
= 16x - x2 = 48
= - 16x + x2 + 48 = 0
= + x2 - 16x + 48 = 0
= + x2 - 12x - 4x + 48 = 0
= x(x - 12) - 4(x - 12) = 0
= (x - 12)(x - 4) = 0
Either x - 12 = 0 therefore x = 12
Or , x - 4 = 0 therefore x = 4
The two numbers are 4 and 12 respectively.
Question 18: Determine the two consecutive multiples of 3 whose product is 270
Solution:
Let the consecutive multiples of 3 are 3xand 3x + 3
According to the question
3x(3x + 3) = 270
= x(3x + 3) = 90
= 3x2 + 3x = 90
= 3x2 + 3x - 90 = 0
= x2 + x - 30 = 0
= x2 + 6x - 5x - 30 = 0
= x(x + 6) - 5(x + 6) = 0
= (x + 6)(x - 5) = 0
Either x + 6 = 0 therefore x = - 6
Or , x - 5 = 0 therefore x = 5
Considering the positive value of x
x = 5
3x = 15
3x + 3 = 18
The two consecutive multiples of 3 are 15 and 18 respectively.
Question 19: The sum of a number and its reciprocal is 17/4 . find the numbers.
Solution:
Lethe number be x
According to the question
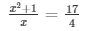
= 4(x2 + 1) = 17x
= 4x2 + 4 - 17x = 0
= 4x2 + 4 - 16x - x = 0
= 4x(x - 4) - 1(x - 4) = 0
= (4x - 1)(x - 4) = 0
Either x - 4 = 0 therefore x = 4
Or, 4x - 1 = 0 therefore x = 1/4
The value of x is 4
Question 20: A two digit is such that the products of its digits is 8when 18 is subtracted from the number, the digits interchange their places. Find the number?
Solution:
Let the digits be x and x - 2 respectively.
The product of the digits is 8
According to the question
x(x - 2) = 8
= x2 - 2x - 8 = 0
= x2 - 4x + 2x - 8 = 0
= x(x - 4) + 2(x - 4) = 0
Either x - 4 = 0 therefore x = 4
Or , x + 2 = 0 therefore x = - 2
Considering the positive value of x = 4
x - 2 = 2
The two digit number is 42.
Question 21: A two digit number is such that the product of the digits is 12, when 36 is added to the number, the digits interchange their places .find the number.
Solution:
Let the tens digit be x
Then, the unit digit = 12/x
Therefore the number = 10x + 12/x
And, the number obtained by interchanging the digits = x + 120/x
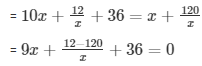
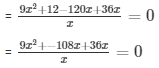
= 9(x2 + 4x - 12) = 0
= (x2 + 4x - 12) = 0
= x2 + 6x - 2x - 12 = 0
= x(x + 6) - 2(x + 6) = 0
= (x - 2)(x + 6) = 0
Either x - 2 = 0 therefore x = 2
Or, x + 6 = 0 therefore x = - 6
Since a digit can never be negative. So x = 2
The number is 26.
Question 22: A two digit number is such that the product of the digits is 16 when 54 is subtracted from the number, the digits are interchanged. Find the number.
Solution:
Let the two digits be:
Tens digit be x
Units digit be 16/x
Numbers = 10x + 16/x ……………………….(i)
Number obtained by interchanging = 10(10x + 16/x)
10x + 16/x – 10(10x + 16/x) = 54
= 10x2 + 16 - 160 + x2 = 54
= 9x2 - 54x - 144 = 0
= x2 - 6x - 16 = 0
= x2 - 8x + 2x - 16 = 0
= x(x - 8) + 2(x - 8) = 0
= (x - 8)(x + 2) = 0
Either x - 8 = 0 therefore x = 8
Or, x + 2 = 0 therefore x = - 2
A digit can never be negative so x = 8
Hence by putting the value of x in the above equation (i) the number is 82.
Question 23: Two numbers differ by 3 and their product is 504. Find the numbers.
Solution:
Let the numbers be x and x - 3 respectively.
According to the question
= x(x - 3) = 504
= x2 - 3x - 504 = 0
= x2 - 24x + 21x - 504 = 0
= x(x - 24) + 21 (x - 24) = 0
= (x - 24)(x + 21) = 0
Either x - 24 = 0 therefore x = 24
Or , x + 21 = 0 , therefore x = - 21
x = 24 and x = - 21
x - 3 = 21 and x - 3 = - 24
The two numbers are 21 a nd 24 and - 21 and - 24 respectively.
Question 24: Two numbers differ by 4 and their product is 192. Find the numbers.
Solution:
Let the two numbers be x and x - 4 respectively
Given that the product of the numbers is 192
According to the question
= x(x - 4) = 192
= x2 - 4x - 192 = 0
= x2 - 16x + 12x - 192 = 0
= x(x - 16) + 12(x - 16) = 0
= (x - 16) (x + 12) = 0
Either x - 16 = 0 therefore x = 16
Or, x + 12 = 0 therefore x = - 12
Considering only the positive value of x
x = 16S
x - 4 = 12
The two numbers are 12 and 16 respectively.
Question 25: A two digit number is 4 times the sum of its digits and twice the product of its digits. Find the numbers.
Solution:
Let the digit in the tens and the units place be x and y respectively.
Then it is represented by 10x + y
According to the question,
10x + y = 4(sum of the digits) and 2xy
10x + y = 4(x + y) and 10x + y = 2xy
10x + y = 4x + 4y and 10x + y = 2xy
6x - 3y = 0 and 10x + y - 2xy = 0
y = 2x and 10x + 2x - 2x(2x) = 0
12x = 4x2
4x(x - 3) = 0
Either 4x = 0 therefore x = 0
Or, x - 3 = 0 therefore x = 3
We have y = 2x
When x = 3 , y = 6
Question 26: The sum of the squares of two positive integers is 208. If the square of the large number is 18 times the smaller. Find the numbers.
Solution:
Let the smaller number be x
Then, square of the large number be = 18x
Also, square of the smaller number be = x2
It is given that the sum of the square of the integer is 208.
Therefore,
= x2 + 18x = 208
= x2 + 18x - 208 = 0
Applying factorization theorem,
= x2 + 26x - 8x - 208 = 0
= x(x + 26) - 8(x + 26) = 0
= (x + 26)(x - 8) = 0
Either x + 26 = 0 therefore x = - 26
Or, x - 8 = 0 therefore x = 8
Considering the positive number, therefore x = 8.
Square of the largest number = 18x = 18*8 = 144
Largest number = 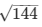 = 12
= 12
Hence the numbers are 8 and 12 respectively.
Question 27: The sum of two numbers is 18. The sum of their reciprocal is 1/4 .find the numbers.
Solution:
Let the numbers be x and (18 - x) respectively.
According to the given hypothesis,
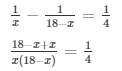
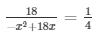
= 72 = 18x - x2
= x2 - 18x + 72 = 0
Applying factorization theorem, we get,
= x2 - 6x - 12x + 72 = 0
= x(x - 6) - 12(x - 6) = 0
= (x - 6)(x - 12) = 0
Either, x = 6
Or, x = 12
The two numbers are 6 and 12 respectively.
Question 28: The sum of two numbers a and b is 15 and the sum of their reciprocals 1/a and 1/b is 3/10. Find the numbers a and b.
Solution:
Let us assume a number x such that
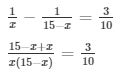
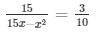
= 3x2 - 45x + 150 = 0
= x2 - 15 x + 50 = 0
Applying factorization theorem,
= x2– 10x - 5x + 50 = 0
= x(x - 10) - 5(x - 10) = 0
= (x - 10)(x - 5) = 0
Either, x - 10 = 0 therefore x = 10
Or, x - 5 = 0 therefore x = 5
Case (i)
If x = a , a = 5 and b = 15 - x , b = 10
Case (ii)
If x = 15 - a = 15 - 10 = 5 ,
x = a = 10 , b = 15 - 10 = 5
Hence when a = 5 , b = 10
a = 10 , b = 5
Question 29: The sum of two numbers is 9. The sum of their reciprocal is 1/2.find the numbers.
Solution:
Given that the sum of the two numbers is 9
Let the two number be x and 9 - x respectively
According to the question
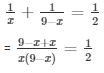
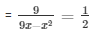
= 9x - x2 = 18
= x2 - 9x + 18 = 0
= x2 - 6x - 3x + 18 = 0
= x(x - 6) - 3(x - 6) = 0
= (x - 6)(x - 3) = 0
Either x - 6 = 0 therefore x = 6
Or x - 3 = 0 therefore x = 3
The two numbers are 3 and 6 respectively
Question 30: Three consecutive positive integers are such that the sum of the squares of the first and the product of the other two is 46. Find the integers.
Solution:
Let the consecutive positive integers be x , x + 1, x + 2 respectively
According to the question
X2 + (x + 1)(x + 2) = 46
= x2 + x2 + 3x + 2 = 46
= 2 x2 + 3x + 2 = 46
= 2 x2 + 3x + 2 - 46 = 0
= 2 x2 - 8x + 11x + - 44 = 0
= 2x(x - 4) + 11(x - 4) = 0
= (x - 4)(2x + 11) = 0
Either x - 4 = 0 therefore x = 4
Or, 2x + 11 = 0 therefore x = −11/2
Considering the positive value of x that is x = 4
The three consecutive numbers are 4 , 5 and 6 respectively
Question 31: The difference of squares of two numbers is 88. If the large number is 5 less than the twice of the smaller, then find the two numbers
Solution:
Let the smaller number be x and larger number is 2x - 5
It is given that the difference of the squares of the number is 88
According to the question
(2x - 5)2 - x2 = 88
= 4x2 + 25 - 20x - x2 = 88
= 3x2 - 20x - 63 = 0
= 3x2 - 27x + 7x - 63 = 0
= 3x(x - 9) + 7(x - 9) = 0
= (x - 9)(3x + 7) = 0
Either x - 9 = 0 therefore x = 9
Or, 3x + 7 = 0 therefore x = −7/3
Since a digit can never be negative so x = 9
Hence the number is 2x - 5 = 13
The required numbers are 9 and 13 respectively
Question 32: The difference of squares of two numbers is180. The square of the smaller number is 8 times the larger number. Find the two numbers
Solution:
Let the number be x
According to the question
X2 - 8x = 180
X2 - 8x - 180 = 0
= X2 + 10x - 18x - 180 = 0
= x(x + 10) - 18(x - 10) = 0
= (x - 18)(x + 10) = 0
Either x - 18 = 0 therefore x = 18
Or, x + 10 = 0 therefore x = - 10
Case (i)
X = 18
8x = 144
Larger number = 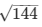 = 12
= 12
Case (ii)
X = - 10
Square of the larger number 8x = - 80
Here in this case no perfect square exist
Hence the numbers are 18 and 12 respectively .
|
5 videos|292 docs|59 tests
|
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















