Ex-8.9 Quadratic Equations, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Q.1: Ashu is x years old while his mother Mrs. Veena is x2 years old. Five years hence Mrs. Veena will be three times old as Ashu. Find their present ages.
Sol:
Given that Ashu’s present age is x years and his mother Mrs. Veena is x2 years
Then, acc. to question,
Five years later, Ashu is (x + 5) years
And his mother Mrs. Veena is (x2 + 5) years
So,
x2 + 5 = 3(x + 5)
x2 + 5 = 3x + 15
x2 + 5 – 3x – 15 = 0
x2 – 5x + 2x + 10 = 0
x(x – 5) + 2(x – 5) = 0
(x – 5)(x + 2) = 0
X = 5 or x = – 2
Since, the age can never be negative
Therefore, ashu’s present age is 5 years and his mother’s age is 25 years.
Q.2: The sum of the ages of a man and his son is 45 years. Five years ago, the product of their ages was four times the man’s age at the time. Find their present ages.
Sol:
Let the present age of the man be x years
Then, present age of his son is = (45 – x) years
Five years ago, man’s age = (x – 5) years
And his son’s age = (45 – x – 5) = (40 – x) years
Then, acc. To question,
(x – 5)(40 – x) = 4(x – 5)
40x – x2 + 5x – 200 = 4x – 20
-X2 + 45x – 200 = 4x – 20
-x2 + 45x – 200 – 4x + 20 = 0
-x2 + 41x – 180 = 0
x2 – 36x – 5x + 180 = 0
x(x – 36) – 5(x – 36) = 0
(x – 36)(x – 5) = 0
x = 36 or x = 5
But, the father’s age can never be 5 years
Therefore, when x = 36,
45 – x = 45 – 36 = 9
Hence, man’s present age is 36 years and his son’s age is 9 years.
Q.3: The product of Shikha’s age five years ago and her age 8 years later is 30, her age at both times being given in years. Find her present age.
Sol:
let the present age of shikha be x years
Then, 8 years later, age of her = (x + 8) years
Five years ago, her age = (x – 5) years
Then, acc. To question,
(x – 5)(x + 8) = 30
x2 + 8x – 5x – 40 = 30
x2 + 3x – 40 – 30 = 0
x2 + 3x – 70 = 0
x(x – 7) + 10(x – 7) = 0
(x – 7)(x + 10) = 0
x = 7 or x = -10
Since, the age can never be negative
Heence, the present age of shikha is = 7 years.
Q.4: The product of Ramu’s age (in years) five years ago and his age (in years) nine years later is 15. Determine Ramu’s present age.
Sol:
let the present age of ramu be x years
Then, 9 years later, age of her = (x + 9) years
Five years ago, her age = (x – 9) years
Then, acc. to question,
(x – 5)(x + 5) = 15
x2 + 9x – 5x – 45 = 15
x2 + 4x – 45 – 15 = 0
x2 + 4x – 60 = 0
x2 – 6x + 10x – 60 = 0
x(x – 6) + 10(x – 6) = 0
(x – 6)(x + 10) = 0
x = 6 or x = – 10
Since, the age can be never be negative
Therefore, the present age of ramu is = 6 years
Q.5: Is the following situation possible? if so, determine their present ages.
The sum of the ages of two friends is 20 years. four years ago, the product of their ages in years was 48.
Sol:
let the present age of two friends be x years and (20 – x) years respectively
Then, 4 years later, the age of two friends will be (x – 4) years and (20 – x – 4) years
Then, acc. To the question
(x – 4)(20 – x – 4) = 48
(x – 4)(16 – x) = 48
16x – x2 – 64 + 4x = 48
– x2 + 20x – 64 – 48 = 0
x2 – 20x + 112 = 0
Let the discriminant of the above quadratic eqn.
D = b2 – 4ac
Here, a = 1, b = -20, c = 112
D = (-20)2 – (4x1x112) = 400 – 448 = – 48
Since, D < 0
The above question does not have real roots.
Hence, the given situation is not possible.
Q.6: A girl is twice as old as her sister. Four years hence, the product of their ages (in years) will be 160. Find their present ages.
Sol:
let the present age of girl be x years then, age of her sister (x/2) years
Then, 4 years later, age of girl = (x + 4) years and her sister’s age be (x/2 + 4) years
Then, acc. to the question,
(x + 4)(x/2 + 4) = 160
(x + 4) (x + 8) = 160×2
x2 + 8x + 4x + 32 = 320
x2 + 12x – 288 = 0
x2 – 12x + 24x – 288 = 0
x(x – 12) + 24(x – 12) = 0
(x – 12) (x + 24) = 0
x = 12 or x = – 24
Since, the can never be negative,
Therefore, the present age of the girl is = 12 years.
And her sister’s age will be,
x/2 = 12/2 = 6 years.
Q.7: The sum of the reciprocals of Rehman’s ages (in years) 3 years ago and 5 years from now is 1/3. Find his present age.
Sol: let the present age of Rehman be x years
Then, 8 years late, age of her = (x + 5) years
Five years ago, her age = (x – 3) years
Acc. To question,
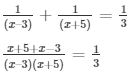
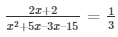
x2 + 2x – 15 = 6x + 6
x2 + 2x – 15 – 6x – 6 = 0
x2 – 4x – 21 = 0
x2 – 7x + 3x – 21 = 0
x(x – 7) + 3(x – 7) = 0
(x – 7)(x + 3) = 0
x = 7 or x = -3
Since, the age can never be negative
Therefore, the present age of Rehman be = 7 years.
|
5 videos|292 docs|59 tests
|
FAQs on Ex-8.9 Quadratic Equations, Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. What are quadratic equations? |  |
| 2. How can I solve quadratic equations using the quadratic formula? |  |
| 3. Can quadratic equations have more than two solutions? |  |
| 4. How can I determine the nature of the roots of a quadratic equation? |  |
| 5. Can quadratic equations only have real solutions? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















