Ex-8.11 Quadratic Equations, Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Question 1:
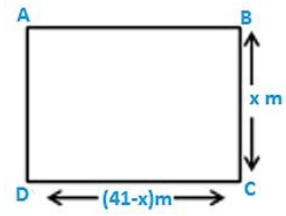
The perimeter of the rectangular field is 82m and its area is 400m2.find the breadth of the rectangle?
Sol:
Let the breadth of the rectangle be (x) m
Given,
Perimeter = 82 m
Area = 400 m2
Perimeter of a rectangle = 2(length + breadth)
82 = 2(length + x)
41 = (length + x)
Length = (41 - x) m
We know,
Area of the rectangle = length * breadth
400 = (41 - x) (x)
400 = 41x - x2
= x2 - 41x + 400 = 0
= x2 - 25x - 16x + 400 = 0
= x(x - 25) - 16(x - 25) = 0
= (x - 16)(x - 25) = 0
Either x - 16 = 0 therefore x = 16
Or, x - 25 = 0 therefore x = 25
Hence the breadth of the above mentioned rectangle is either 16 m or 25 m respectively.
Question 2:
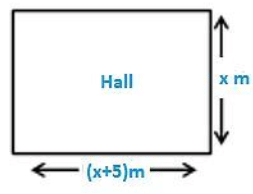
The length of the hall is 5 m more than its breadth. If the area of the floor of the hall is 84 m2 , what is the length and breadth of the hall?
Sol:
Le the breadth of the rectangle be x m
Let the length of the hall is 5 m more than its breadth = ( x + 5 ) m
Also given that,
Area of the hall is = 84 m2
The shape of the hall is rectangular
Area of the rectangular hall = length * breadth
84 = x(x + 5)
= x2 + 5x - 84 = 0
= x2 + 12x - 7x - 84 = 0
= x(x + 12) - 7(x + 12) = 0
= (x + 12)(x - 7) = 0
Either x + 12 = 0 therefore x = - 12
Or, x - 7 = 0 therefore x = 7
Since the value of x cannot be negative
So x = 7
= x + 5 = 12
The length and breadth of the rectangle is 7 and 12 respectively.
Question 3: Two squares have sides x and (x + 4) cm. The sum of their area is 656 cm2 . Find the sides of the square.
Sol:
Let S1 and S2 be the two square
Let x cm be the side square S1 and (x + 4) cm be the side of the square S2 .
Area of the square S1 = x2 cm2
Area of the square S2 = ( x + 4)2 cm2
According to the question,
Area of the square S1 + Area of the square S2 = 656 cm2
= x2 cm2 + ( x + 4)2 cm2 = 656 cm2
= x2 + x2 + 16 + 8x - 656 = 0
= 2 x2 + 16 + 8x - 656 = 0
= 2 (x2 + 4x - 320) = 0
= x2 + 4x - 320 = 0
= x2 + 20x - 16x - 320 = 0
= x(x + 20) - 16(x + 20) = 0
= (x + 20)(x - 16) = 0
Either x + 20 = 0 therefore x = - 20
Or, x - 16 = 0 therefore x = 16
Since the value of x cannot be negative so the value of x = 16
The side of the square S1 = 16 cm
The side of the square S2 = 20 cm
Question 4: The area of the right - angled triangle is 165 cm2. Determine the base and altitude if the latter exceeds the former by 7m.
Sol:
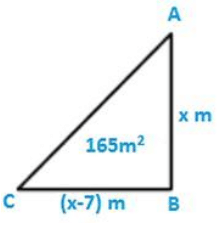
Let the altitude of the right angles triangle be denoted by x m
Given that the altitude exceeds the base by 7 m = x - 7 m
We know
Area of the triangle = 12×base×altitude
= 165 = 12×(x−7)×x
= x(x - 7) = 330
= x2 - 7x - 330 = 0
= x2 - 22x + 15x - 330 = 0
= x(x - 22) + 15(x - 22) = 0
= (x - 22)(x + 15) = 0
Either x - 22 = 0 therefore x = 22
Or, x + 15 = 0 therefore x = - 15
Since the value of x cannot be negative so the value of x = 22
= x - 7 = 15
The base and altitude of the right angled triangle are 15 cm and 22 cm respectively.
Question 5: Is it possible to design a rectangular mango grove whose length is twice its breadth and area is 800 m2 .find its length and breadth.
Sol:
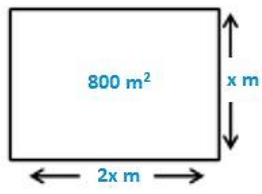
Let the breadth of the rectangular mango grove be x m
Given that length of rectangle is twice of its breadth
Length = 2x
Area of the grove = 800 m2
We know,
Area of the rectangle = length * breadth
= 800 = x(2x)
= 2x2 - 800 = 0
= x2 - 400 = 0 = x2 = 400 = x = 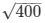 = 20
= 20
Breadth of the rectangular groove is 20 m
Length of the rectangular groove is 40 m
Yes, it is possible to design a rectangular groove whose length is twice of its breadth.
Question 6: Is it possible to design a rectangular park of perimeter 80 m and area 400 m2? If so find its length and breadth.
Sol:
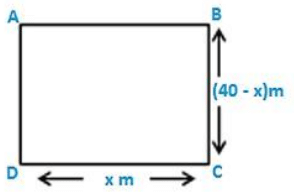
In order to prove the given condition let us assume that the length of the rectangular park is denoted by x m
Given that,
Perimeter = 8 cm
Area = 400 cm 2
Perimeter of the rectangle = 2(length + breadth)
80 = 2(x + breadth)
Breadth = (40 - x) m
We know,
Area of the rectangle = (length) (breadth)
= 400 = x(40 - x)
= 40x - x2 = 400
= x2 - 40x + 400 = 0
= x2 - 20x - 20x + 400 = 0
= x(x - 20) - 20(x - 20) = 0
= (x - 20)(x - 20) = 0
= (x - 20)2 = 0
= x - 20 = 0 therefore x = 20
Length of the rectangular park is = 20 m
Breadth of the rectangular park = (40 - x) = 20 m
Yes, it is possible to design a rectangular Park of perimeter 80 m and area 400m2
Question 7: Sum of the area of the square is 640 m2.if the difference of their perimeter is 64 m, find the sides of the two squares.
Sol:
Let the two squares be S1 and S2 respectively. let he sides of the square S1 be x m and the sides of the square S2 be y m
Given that the difference of their perimeter is 64 m
We know that the
Perimeter of the square = 4(side)
Perimeter of the square S1 = 4x m
Perimeter of the square S2 = 4y m
Now, difference of their perimeter is 64 m
= 4x - 4y = 64
x - y = 16
x = y + 16
Also, given that the sum of their two areas
= area of the square 1 + area of the square 2
= 640 = x2 + y2
= 640 = (y + 16)2 + y2
= 2y2 + 32y + 256 - 640 = 0
= 2y2 + 32y - 384 = 0
= 2(y2 + 16y - 192) = 0
= y2 + 16y - 192 = 0
= y2 + 24y - 8y - 192 = 0
= y(y + 24) - 8(y + 24) = 0
= (y + 24)(y - 8) = 0
Either y + 24 = 0 therefore y = - 24
Or, y - 8 = 0 therefore y = 8
Since the value of y cannot be negative so y = 8
Side of the square 1 = 8 m
Side of the square 2 = 8 + 16 = 24 m
The sides of the squares 1 and 2 are 8 and 24 respectively.
|
5 videos|292 docs|59 tests
|
FAQs on Ex-8.11 Quadratic Equations, Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. What are quadratic equations? |  |
| 2. How do I solve quadratic equations using the quadratic formula? |  |
| 3. Can quadratic equations have more than two solutions? |  |
| 4. What is the discriminant of a quadratic equation? |  |
| 5. Are there any other methods to solve quadratic equations apart from the quadratic formula? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|

















