Ex-9.6 Arithmetic Progressions (Part - 1), Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Question 1. Find the sum of the following Arithmetic Progression.
(i) 50, 46, 42,… To 10 terms
(ii) 1, 3, 4, 7, . . . 26 to 12 terms.
(iii) 3,9/2,6,15/2,.... to 25 terms.
(iv) 41, 36, 31, . . . To 12 terms.
(v) a + b, a – b, a -3b,… To 22 terms.
(vi) (x – y)2 , (x2, y2), (x + y)2, . . . to n terms.
(vii) 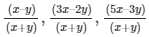 ,...tonterms
,...tonterms
(viii) -26, -24, -22, . . . to 36 terms.
Solution:-
In the given problem, we need to find the sum of terms for different A.P.
So, here we use the following formula for the sum of n terms of an A.P.,
Sn = n/2[2a + (n – 1)d]
Where; a = first term for the given A.P.
d = common difference of the given A.P. n = number of terms
(i) 50, 46, 42,… To 10 terms
Common difference of the A.P. (d)
= a2 – a1
= 46 – 50
= -4
Number of terms (n) = 10
First term for the given A.P. (a) = 50
So, using the formula we get,
S10 = 10/2[2(50) + (10 – 1)(−4)]
= (5) [ 100 + (9)(-4) ]
= (5) [ 100 – 36 ]
= (6) [64]
= 320
Therefore, the sum of first 10 terms of the given A.P. is 320
(ii) 1, 3, 4, 7, . . . 26 to 12 terms.
Common difference of the A.P. (d)
= a2 – a1
= 3 – 1
= 2
Number of terms (n) = 12
First term (a) = 1
So, using the formula we get,
S12 = 12/2[2(1) + (12 – 1)(2)]
= (6) [ 2 + (11)(2) ]
= (6) [ 2 + 22 ]
= (6) [24]
= 144
Therefore, the sum of first 10 terms of the given A.P. is 144
(iii) 3,9/2,6,15/2,.... to 25 terms.
Common difference here is (d): a2 – a1
= 9/2 – 3
= (9 – 6)/2
= 3/2
Number of terms (n) = 25
First term of the A.P. (a) = 3
So, using the formula we get,
S25 = 25/2[2(3) + (25 – 1)(3/2)]
= (25/2)[6 + (24)(3/2)]
= (25/2)[6 + (72/2)]
= (25/2)[6 + 36]
= (25/2)[42]
= ( 25 ) ( 21 )
= 525
Therefore, the sum of first 12 terms for the given A.P. is 162.
(iv) 41, 36, 31, . . . To 12 terms.
Common Difference of the A.P. (d) = a2 – a1
= 36 – 41
= -5
Number of terms (n) = 12
First term for the given A.P. (a) = 41
So, using the formula we get,
S12 = 12/2[2(41) + (12 – 1)(−5)]
= (6) [82 + (11) (-5)]
= (6) [82 – 55]
= (6) [27]
= 162
Therefore, the sum of first 12 terms for the given A.P. 162
(v) a + b, a – b, a -3b,… To 22 terms.
Common difference of the A.P. (d) = a2 – a1
= (a – b) – (a + b)
= a – b – a – b
= -2b
Number of terms (n) = 22
First term for the given A.P. (a) = a + b
So, using the formula we get,
S22 = 22/2[2(a + b) + (22 – 1)(−2b)]
= (11)[ 2(a + b) + (22 – 1)( -2b ) ]
= (11)[ 2a + 2b + (21)(-2b) ]
= (11)[ 2a + 2b – 42b ]
= (11)[2a – 40b]
= 22a – 40b
Therefore, the sum of first 22 terms for the given A.P. is: 22a – 40b
(vi) (x – y)2 , (x2, y2), (x + y)2, . . . to n terms.
Common difference of the A.P. (d) = a2 – a1
= (x2 – y2) – (x – y)2
= x2 + y2 – (x2 + y2 – 2xy)
= 2xy
Number of terms (n) = n
First term for the given A.P. (a) = (x – y)2
So, using the formula, we get.
Sn = n/2[2(x – y)2 + (n – 1)2xy]
Now, taking 2 common from both the terms inside bracket, we get
= n/2(2)[(x – y)2 + (n – 1)xy]
= (n)[ ( x – y )2 + ( n – 1 )xy ]
Therefore, the sum of first n terms of the given A.P. is (n)[ ( x – y )2 + ( n – 1 )xy ]
(vii) 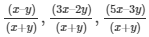 ...tonterms
...tonterms
Common difference of the A.P. (d) = a2 – a1
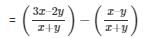
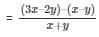
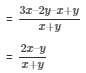
So, using the formula we get,
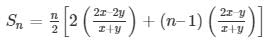
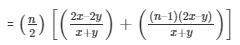
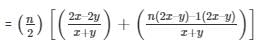
On further solving, we get
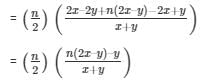
Therefore, the sum of first n terms for the given A.P. is 
(viii) -26, -24, -22, . . . to 36 terms.
Common difference of the A.P. (d) = a2 – a1
= (-24) – (-26)
= -24 + 26
= 2
Number of terms (n) = 36
First term for the given A.P. (a) = -26
So, using the formula we get,
Sn = (36/2)[2(−26) + (36 – 1)(2)]
= (18) [ -52 + (35) (2)
= (18) [-52 + 70]
= (18) (18)
= 324
Therefore, the sum of first 36 terms for the given A.P. is 324
Question 2. Find the sum to n term of the A.P. 5, 2, -1, -4, -7, . . .
Solution: In the given problem, we need to find the sum of the n terms of the given A.P.
5,2,-1,-4,-7,….
So, here we use the following formula for the sum of n terms of an A.P.,
Sn = n/2[2a + (n – 1)d]
Where; a = first term for the given A.P.
d = common difference of the given A.P.
and n = number of terms
For the given A.P. (5,2,-1,-4,-7,…),
Common difference of the A.P. (d) = a2 – a1
= 2 – 5
= -3
Number of terms (n) = n
First term for the given A.P. (a) = 5
So, using the formula we get,
Sn = n/2[2(5) + (n – 1)( – 3)]
= n/2[10 + (−3n + 3)]
= n/2[10 – 3n + 3]
= n/2[13 – 3n]
Therefore, the sum of first n terms for the given A.P. is n/2[13 – 3n]
Question 3. Find the sum of n terms of an A.P. whose nth terms is given by an = 5 – 6n.
Solution: Here, we are given an AP, whose nth term is given by the following expression,
an = 5 – 6n
So, here we can find the sum of the n terms of the given A.P., using the formula,
Sn = (n/2)(a + l)
Where, a = the first term
l = the last term
So, for the given AP,
The first term (a) will be calculated using n = 1 in the given equation for nth term of A.P.
a = 5 – 6(1)
= 5 -6
= -1
Now, the last term (l) or the nth term is given
an = 5 – 6n
So, on substituting the values in the formula for the sum of n terms of an AP., we get,
Sn = (n/2)[(−1) + 5−6n]
= (n/2)[4 – 6n]
= (n/2)(2)[2 – 3n]
= (n) (2 – 3n)
Therefore, the sum of the n terms of the given A.P. is (n) (2 – 3n)
Question 5. Find the sum of first 15 term of each of the following sequences having nth term as
(i) an = 3 + 4n
(ii) bn = 5 + 2n
(iii) xn = 6 – n
(iv) yn = 9 -5n
Solution:
(i) Here, we are given an A.P. whose nth term is given by the following expression,
an = 3 + 4n
We need to find the sum of first 15 term & n ,
So, here we can find the sum of the n terms of the given A.P.,
using the formula,
Sn = n/2(a + l)
Where, a = the first term
l = the last term
So, for the given AP,
The first term (a) will be calculated using n = 1 in the given equation for nth term of A.P.
a = 3 + 4(1)
= 3 + 4
= 7
Now, the last term (l) or the nth term is given
l = an = 3 + 4n
So, on substituting the values in the formula for the sum of n terms of an A.P, we get,
Sn = 15/2(7 + 3 + 4(15))
= 15/2(10 + 60)
= 15/2(70)
= (15)(35)
= 525
Therefore, the sum of the 15 terms of the given A.P. is S15 = 525
(ii) Here, we are given an A.P. whose nth term is given by the following expression,
bn = 5 + 2n
We need to find the sum of first 15 term & n ,
So, here we can find the sum of the n terms of the given A.P.,
using the formula,
Sn = n/2(a + l)
Where, a = the first term
l = the last term
So, for the given AP,
The first term (a) will be calculated using n = 1 in the given equation for nth term of A.P.
b = 5 + 2(1)
= 5 + 2
= 7
Now, the last term (l) or the nth term is given
l = bn = 5 + 2n
So, on substituting the values in the formula for the sum of n terms of an A.P, we get,
Sn = 15/2(7 + 5 + 2(15))
= 15/2(12 + 30)
= 15/2(42)
= (15) (21)
= 315
Therefore, the sum of the 15th term of the given A.P. is 315
(iii) Here, we are given an A.P. whose nth term is given by the following expression,
xn = 6 – n
We need to find the sum of first 15 term & n ,
So, here we can find the sum of the n terms of the given A.P.,
using the formula,
Sn = n/2(a + l)
Where, a = the first term
l = the last term
So, for the given AP,
The first term (a) will be calculated using n = 1 in the given equation for nth term of A.P.
b = 6 – 1
= 5
Now, the last term (l) or the nth term is given
l = xn = 6 – n
So, on substituting the values in the formula for the sum of n terms of an A.P, we get,
Sn = 15/2((5) + 6 – (15))
= 15/2(11 – 15)
= 15/2(−4)
= (15) (-2)
= -30
Therefore, the sum of the 15 terms of the given A.P. is -30.
(iv) Here, we are given an A.P. whose nth term is given by the following expression,
yn = 9 – 5n
We need to find the sum of first 15 term & n ,
So, here we can find the sum of the n terms of the given A.P.,
using the formula,
Sn = n/2(a + l)
Where, a = the first term
l = the last term
So, for the given AP,
The first term (a) will be calculated using n = 1 in the given equation for nth term of A.P.
b = 9 – 5 (1)
= 9 – 5
= 4
Now, the last term (l) or the nth term is given
l = bn = 9 – 5n
So, on substituting the values in the formula for the sum of n terms of an A.P, we get,
Sn = 15/2((4) + 9 – 5(15))
= 15/2(13 – 75)
= 15/2( – 62)
= (15) (-31)
= -465
Therefore, the sum of the 15 terms of the given A.P. is -465
Question 6. Find the sum of first 20 terms the sequence whose nth term is an = An + B.
Solution: Here, we are given an A.P. whose nth term is given by the following expression
an = An + B
We need to find the sum of first 20 terms.
So, here we can find the sum of the n terms of the given A.P.,
using the formula,
Sn = n/2(a + l)
Where, a = the first term
l = the last term
So, for the given AP,
The first term (a) will be calculated using n = 1 in the given equation for nth term of A.P.
a = A(1) + B
= A + B
Now, the last term (l) or the nth term is given
l = an = An + B
So, on substituting the values in the formula for the sum of n terms of an A.P., we get,
S20 = 20/2((A + B) + A(20) + B)
= 10[ 21A + 2B ]
= 210A + 20B
Therefore, the sum of the first 20 terms of the given A.P. is 210A + 20B
Question 7. Find the sum of first 25 terms of an A.P whose nth term is given by an = 2 – 3n.
Solution: Here, we are given an A.P. whose nth term is given by the following expression,
an = 2 -3n
We need to find the sum of first 25 terms.
So, here we can find the sum of the n terms of the given AP., using the formula,
Sn = n/2(a + l)
Where, a = the first term
l = the last term
So, for the given AP,
The first term (a) will be calculated using n = 1 in the given equation for nth term of A.P.
a = 2 -3(1)
= 2-3
= -1
Now, the last term (1) or the nth term is given l = an = 2 – 3n
So, on substituting the values in the formula for the sum of n terms of an AP., we get,
S25 = 25/2[(−1) + 2 – 3(25)]
= 25/2[1 – 75]
= (25) (-37)
= -925
Therefore, the sum of the 25 terms of the given A.P. is -925
Question 8. Find the sum of first 25 terms of an A.P whose nth term is given by an = 7 – 3n.
Solution: Here, we are given an AP. whose nth term is given by the following expression,
an = 7 – 3n.
We need to find the sum of first 25 terms.
So, here we can find the sum of the n terms of the given AP., using the formula,
Sn = n/2(a + l)
Where, a = the first term
l = the last term
So, for the given AP,
The first term (a) will be calculated using n = 1 in the given equation for nth term of A.P.
a = 7 – 3
= 4
Now, the last term (l) or the nth term is given
l = an = 7 – 3n
So, on substituting the values in the formula for the sum of n terms of an AP., we get,
Sn = 25/2[(4) + 7 – 3(25)]
= 25/2[11 – 75]
= 25/2[−64]
= (25)(−32)
= −800
Therefore, the sum of the 25 terms of the given A.P. is Sn = -800
Question 9. If the sum of a certain number of terms starting from first term of an A.P. is 25, 22, 19, . . . , is 116. Find the last term.
Solution:- In the given problem, we have the sum of the certain number of terms of an A.P. and we need to find the last term for that A.P.
So here, let us first find the number of terms whose sum is 116.
For that, we will use the formula,
Sn = n/2[2a + (n – 1)d]
Where; a = first term for the given A.P.
d = common difference of the given A.P.
n = number of terms
So for the given A.P(25, 22, 19,…)
The first term (a) = 25
The sum of n terms Sn = 116
Common difference of the A.P. (d) = a2 – a1
= 22-25
= -3
So, on substituting the values in the formula for the sum of n terms of an A.P., we get,
⇒ 116 = n/2[2(25) + (n – 1)( – 3)]
⇒ (n/2)[50 + (−3 + 3)]
⇒ (n/2)[53 – 3n]
⇒ 116 X 2 = 53n – 3n2
So, we get the following quadratic equation, 3n2 – 53n + 232 = 0
On solving by splitting middle term, we get,
⇒ 3n2 – 24n – 29n + 232 = 0
⇒ 3n( n – 8 ) – 29 ( n – 8 ) = 0
⇒ (3n – 29) ( n – 8 ) = 0
Further,
3n – 29 = 0
⇒ n = 29/3
Also,
n – 8 = 0
⇒ n = 8
Since, n cannot be a fraction, so the number of terms is 8.
So, the term is:
a8 = a1 + 7d
= 25 + 7(-3)
= 25 – 21
= 4
Therefore, the last term of the given A.P. such that the sum of the terms is 116 is 4.
Question 10.
(i). How many terms of the sequence 18, 16, 14…. should be taken so that their sum is 0 (Zero).
(ii). How many terms are there in the A.P. whose first and fifth terms are -14 and 2 respectively and the sum of the terms is 40?
(iii). How many terms of the A.P. 9, 17, 25, . . . must be taken so that their sum is 636?
(iv). How many terms of the A.P. 63, 60, 57, . . . must be taken so that their sum is 693?
(v). How many terms of the A.P. is 27, 24, 21. . . should be taken that their sum is zero?
Solution:
(i) AP. is 18,16,14,…
So here, let us find the number of terms whose sum is 0.
For that, we will use the formula,
Sn = n/2[2a + (n – 1)d]
where; a = first term for the given A.P.
d = common difference of the given A.P.
n = number of terms
The first term (a) = 18
The sum of n terms (Sn) = 0
Common difference of the A.P. (d) = a2 – a1
= 16 – 18
= -2
So, on substituting the values in the formula for the sum of n terms of an AP., we get
⇒ 0 = n/2[2(18) + (n – 1)(−2)]
⇒ 0 = n/2[36 + (−2n + 2)]
⇒ 0 = n/2[38 – 2n]
Further,
n/2
⇒ n = 0
Or, 38 – 2n = 0
⇒ 2n = 38
⇒ n = 19
Since, the number of terms cannot be zero; the number of terms (n) is 19
(ii) Here, let us take the common difference as d.
So, we are given,
First term (a1) = -14
Filth term (a5) = 2
Sum of terms (Sn) = 40
Now,
a5 = a1 + 4d
⇒ 2 = -14 + 4d
⇒ 2 + 14 = 4d
⇒ 4d = 16
⇒ d = 4
Further, let us find the number of terms whose sum is 40.
For that, we will use the formula,
Sn = n/2[2a + (n – 1)d]
Where; a = first term for the given A.P.
d = common difference of the given A.P.
n = number of terms
The first term (a1) = -14
The sum of n terms (Sn) = 40
Common difference of the A.P. (d) = 4
So, on substituting the values in the formula for the sum of n terms of an A.P., we get,
⇒ 40 = n/2[2(−14) + (n – 1)(4)]
⇒ 40 = n/2[−28 + (4n – 4)]
⇒ 40 = n/2[−32 + 4n]
⇒ 40 (2) = – 32n + 4n2
So, we get the following quadratic equation,
4n2 – 32n – 80 = 0
⇒ n2 – 8n + 20 = 0
On solving by splitting the middle term, we get
4n2 – 10n + 2n + 20 = 0
⇒ n( n – 10 ) + 2( n – 10 ) = 0
⇒ ( n + 2 ) ( n – 10) = 0
Further,
n + 2 = 0
⇒ n = -2
Or,
n – 10 = 0
⇒ n = 10
Since the number of terms cannot be negative.
Therefore, the number of terms (n) is 10.
(iii) AP is 9,17,25,…
So here, let us find the number of terms whose sum is 636.
For that, we will use the formula,
Sn = n/2[2a + (n – 1)d]
Where; a = first term for the given A.P.
d = common difference of the given A.P.
n = number of terms
The first term (a) = 9
The sum of n terms (Sn) = 636
Common difference of the A.P. (d) = a2 – a1
= 17 – 9
= 8
So, on substituting the values in the formula for the sum of n terms of an AP.,
we get,
⇒ 636 = n/2[2(9) + (n – 1)(8)]
⇒ 636 = n/2[18 + (8n – 8)]
⇒ 636 (2) = (n) [ 10 + 8n ]
⇒ 1271 = 10n + 8n2
So, we get the following quadratic equation,
⇒ 8n2 + 10n – 1272 = 0
⇒ 4n2 + 5n – 636 = 0
On solving by splitting the middle term, we get,
⇒ 4n2 – 48n + 53n – 636 = 0
⇒ 4n( n – 12 ) – 53( n – 12 ) = 0
⇒ ( 4n – 53 ) ( n – 12 ) = 0
Further,
4n – 53 = 0
⇒ n = 53/4
Or, n – 12 = 0
⇒ n = 12
Since, the number of terms cannot be a fraction.
Therefore, the number of terms (n) is 12.
(iv) A.P. is 63,60,57,…
So here. let us find the number of terms whose sum is 693. For that,
we will use the formula.
Sn = n/2[2a + (n – 1)d]
Where; a = first term for the given A.P.
d = common difference of the given A.P.
n = number of terms
The first term (a) = 63
The sum of n terms (Sn) = 693
Common difference of the A.P. (d) = a2 – a1
= 60 – 63
= -3
So, on substituting the values in the formula for the sum of n terms of an AP we get.
⇒ 693 = n/2[2(63) + (n – 1)(−3)]
⇒ 693 = n/2[163 + (−3n + 3)]
⇒ 693 = n/2[129 – 3n]
⇒ 693 (2) = 129n – 3n2
So. we get the following quadratic equation.
⇒ 3n2 – 129n + 1386 = 0
⇒ n2 – 43n + 462
On solving by splitting the middle term, we get.
⇒ n2 – 22n – 21n + 462 = 0
⇒ n( n – 22 ) -21( n – 22 ) = 0
⇒ ( n – 22) ( n – 21 ) = 0
Further,
n – 22 = 0
⇒ n = 22
Or, n – 21 = 0
⇒ n = 21
Here, 22nd term will be
a22 = a1 + 21d
= 63 + 21( -3 )
= 63 – 63
= 0
So, the sum of 22 as well as 21 terms is 693.
Therefore, the number of terms (n) is 21 or 22
(v) A.P. is 27, 24, 21. . .
So here. let us find the number of terms whose sum is 0. For that,
we will use the formula.
Sn = n/2[2a + (n – 1)d]
Where; a = first term for the given A.P.
d = common difference of the given A.P.
n = number of terms
The first term (a) = 27
The sum of n terms (Sn) = 0
Common difference of the A.P. (d) = a2 – a1
= 24 – 27
= -3
So, on substituting the values in the formula for the sum of n terms of an AP we get.
⇒ 0 = n/2[2(27) + (n – 1)(−3)]
⇒ 0 = (n) [ 54 + ( n – 1 )(-3) ]
⇒ 0 = (n) [ 54 – 3n + 3 ]
⇒ 0 = n [ 57 – 3n ]
Further we have,
n = 0
Or,
57 – 3n = 0
⇒ 3n = 57
⇒ n = 19
The number of terms cannot be zero,
Therefore, the numbers of terms (n) is 19.
Question 11. Find the sum of the first
(i) 11 terms of the A.P. : 2, 6, 10, 14, . . .
(ii) 13 terms of the A.P. : -6, 0, 6, 12, . . .
(iii) 51 terms of the A.P. : whose second term is 2 and fourth term is 8.
Solution: In the given problem,
we need to find the sum of terms for different arithmetic progressions.
So, here we use the following formula for the sum of n terms of an A.P.,
Sn = n/2[2a + (n – 1)d]
Where; a = first term for the given A.P.
d = common difference of the given A.P.
n = number of terms
(i) 2,6,10,14,… To 11 terms.
Common difference of the A.P. (d) = a2 – a1
= 10 – 6
= 4
Number of terms (n) = 11
First term for the given A.P. (a) = 2
So, using the formula we get,
S11 = 11/2[2(2) + (11 – 1)4]
= 11/2[2(2) + (10)4]
= 11/2[4 + 40]
= 11 X 22
= 242
Therefore, the sum of first 11 terms for the given A.P. is 242
(ii) -6, 0, 6, 12, … to 13 terms.
Common difference of the AR (d) = a2 – a1
= 6 – 0
= 6
Number of terms (n) = 13
First term for the given AP (a) = -6
So, using the formula we get,
S13 = 13/2[2(−6) + (13 – 1)6]
= 13/2[(−12) + (12)6]
= 13/2[60]
= 390
Therefore, the sum of first 13 terms for the given AR is 390
(iii) 51 terms of an AP whose a2 = 2 and a4 = 8
Now,
a2 = a + d
2 = a + d …(i)
Also,
a4 = a + 3
8 = a + 3d … (2)
Subtracting (1) from (2), we get
2d = 6
d = 3
Substituting d = 3 in (i), we get
2 = a + 3
⇒ a = -1
Number of terms (n) = 51
First terms for the given A.P.(a) = -1
So, using the formula, we get
Sn = 51/2[2(−1) + (51 – 1)(3)]
= 51/2[−2 + 150]
= 51/2[158]
= 3774
Therefore, the sum of first 51 terms for the A.P. is 3774.
|
5 videos|292 docs|59 tests
|
FAQs on Ex-9.6 Arithmetic Progressions (Part - 1), Class 10, Maths RD Sharma Solutions - Extra Documents, Videos & Tests for Class 10
| 1. What are arithmetic progressions? |  |
| 2. How can we find the nth term of an arithmetic progression? |  |
| 3. Can an arithmetic progression have a common difference of zero? |  |
| 4. How can we find the sum of the first n terms of an arithmetic progression? |  |
| 5. Can an arithmetic progression have a negative common difference? |  |
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|

















