Ex-9.6 Arithmetic Progressions (Part - 3), Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download

Question 20. In an A.P., if the 5^th and 12^th terms are 30 and 65 respectively, what is the sum of first 20 terms ?

Solution:  In the given problem, let us take the first term as a

and the common difference d

Here, we are given that,

a₅ = 30                                                                                                             . . . .(1)

a₁₂ = 65                                                                                                           . . . .(2)

Also, we know,

a_n = a + (n – 1)d

For the 5^th term (n = 5),

a₅ = a + (5 – 1)d

30 = a + 4d                                                      (Using 1)

a = 30 – 4d                                                                                                      . . . .(3)

Similarly, for the 12^th term (n = 12),

a₁₂ = a + (12 – 1) d

65 = a + 11d                                                    (Using 2)

a = 65 – 11d                                                                                                     . . . .(4)
Subtracting (3) from (4), we get,

a – a = (65 – 11d) – (30 – 4d)

0 = 65 – 11d – 30 + 4d

0 = 35 – 7d

7d = 35

d = 5

Now, to find a, we substitute the value of d in (4).

a = 30 – 4(5)

a = 30 – 20

a = 10

So, for the given A.P. d = 5 and a = 10

So, to find the sum of first 20 terms of this A.P.,

we use the following formula for the sum of n terms of an A.P.,

S_n = n/2[2a + (n – 1)d]

Where; a = first term of the given A.P.

d = common difference of the given A.P.

n = number of terms

So, using the formula for n = 20, we get

S₂₀ = 20/2[2(10) + (20 – 1)(5)]

= (10)[ 20 + (19)(5)]

= (10)[20 + 95]

= (10)[115]

= 1150

Therefore, the sum of first 20 terms for the given A.P. is 1150
 

Question 21. Find the sum of first 51 terms of an A.P. whose second and third terms are 14 and 18 respectively.

Solution:  In the given problem,

let us take the first term as a

and the common difference as d.

Here, we are given that,

a₂ = 14                                                                                                 . . . . (1)

a₃ = 18                                                                                                . . . . (2)

Also, we know,

a_n = a + (n – 1)d

For the 2^nd term (n = 2),

⇒ a₂ = a + (2 – 1)d

⇒ 14 = a + d                                                   (Using 1)

⇒ a = 14 – d                                                                            . . . . (3)

Similarly, for the 3^rd term (n = 3),

⇒ a₃ = a + (3 – 1)d

⇒ 18 = a + 2d                                                 (Using 2)

⇒ a = 18 – 2d                                                                          . . . . (4)
Subtracting (3) from (4),

we get, a – a = (18 – 2d) – (14 – d)

0 = 18 – 2d – 14 + d

0 = 4 – d

d = 4

Now, to find a, we substitute the value of d in (4),

a = 14 – 4

a = 10

So, for the given A.P. d = 4 and a = 10

So, to find the sum of first 51 terms of this A.P.,

we use the following formula for the sum of  n terms of an A.P.,

S_n = n/2(2a + (n – 1)d)

Where, a = the first term of the A.P.

d = common difference of the A.P.

n = number of terms

So, using the formula for n = 51, we get

S₅₁ = 51/2[2(10) + (51 – 1)(4)]

=  51/2[20 + (40)4]

=  51/2[220]

= 51 (110)

= 5610

Therefore, the sum of the first 51 terms of the given A.P. is 5610

Question 23. The first term of an A.P. is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.

Solution:  Let a be the first term and d be the common difference.

We know that, sum of first n terms is

S_n = n/2(2a + (n – 1)d)

Where, a = the first term of the A.P.

d = common difference of the A.P.

n = number of terms

Also, nth term = a_n = a + (n – 1)

According to the question,

First term (a) = 5,

last term (a_n) = 45

and sum of n terms (S_n) = 400

Now,

a_n = a + (n – 1)d

⇒ 45 = 5 + (n – 1)d

⇒ 40 = nd – d

⇒ nd – d = 40                                                                               . . . . (1)

Also,

S_n = n/2(2(a) + (n – 1)d)

400 = n/2(2(5) + (n – 1)d)

800 = n (10 + nd – d)

800 = n (10 + 40)                                             from (1)

n = 16                                                                                     . . . . (2)

On substituting (2) in (1), we get

nd – d = 40

16d – d = 40

15d = 40

d =  8/3

Thus, common difference of the given A.P. is 8/3.

Question 24. In an A.P. the first term is 8, n^th term is 33 and the sum of first n term is 123. Find n and the d, the common difference.

Solution:  In the given problem,

we have the first and the nth term of an A.P. along with the sum of the n terms of A.P.

Here, we need to find the number of terms

and the common difference of the A.P

Here,

The first term of the A.P (a) = 8 The

nth term of the A.P (l) = 33

Sum of all the terms S_n = 123

Let the common difference of the A.P. be d.

So, let us first find the number of the terms (n) using the formula,

123 = (n/2)(8 + 33)

123 = (n/2)(41)

n = ((123)(2))/41

n = 246/41

n = 6

Now, to find the common difference of the A.P. we use the following formula,

l = a + (n – 1)d

we get

33 = 8 + (6 – 1)d

33 = 8 + 5d

5d = 25

d = 5

Therefore, the number of terms is n = 6 and the common difference of the A.P. is d = 5.

Question 25. In an A.P. the first term is 22, n^th term is - 11 and the sum of first n term is 66. Find n and the d, the common difference.

Solution:  In the given problem,

we have the first and the nth term of an A.P. along with the sum of the n terms of A.P.

Here, we need to find the number of terms and the common difference of the A.P.

Here,

The first term of the A.P (a) = 22

The nth term of the A.P (l) = - 11

Sum of all the terms S„ = 66

Let the common difference of the A.P. be d.

So, let us first find the number of the terms (n) using the formula,

66 = (n/2)[22 + (−11)]

66 = (n/2)[22 – 11]

(66)(2) = n(11)

6 X 2 = n

n = 12

Now, to find the common difference of the A.P. we use the following formula,

l = a + (n – 1)d

we get,

- 11 = 22 + (12 – 1)d

- 11 = 22 + 11d

11d = - 33

d = - 3

Therefore, the number of terms is n = 12 and the common difference d = - 3

Question 26. The first and the last terms of an A.P. are 7 and 49 respectively. If sum of all its terms is 420, find the common difference.

Solution:  Let a be the first term and d be the common difference.

We know that, sum of first n terms is:

S_n = n/2(2a + (n – 1)d)

Also, n^th term (a_n) = a + (n – 1)d

According to question,

first term (a) = 7

last term (a_n) = 49

and sum of n terms (S_n) = 420

Now,

a_n = a + (n – 1)d

⇒ 49 = 7 + (n – 1)d

⇒ 43 = nd – d

⇒ nd – d = 42                                                                                      . . . . .(1)

Also,

S_n = n/2(2(7) + (n – 1)d)

⇒ 840 = n [14 + nd – d]

⇒ 840 = n [ 14 + 42]                                      [from (1)]

⇒ 840 = 54 n

⇒ n = 15                                                                                             . . . . (2)

on substituting (2) in (1), we get

nd – d = 42

⇒ 15d – d = 42

⇒ 14d = 42

⇒ d = 3

Thus, the common difference of the given A.P. is 3.

Question 28. The sum of first q terms of an A.P. is 162. The ratio of its 6^th term to its 13^th term is 1 : 2. Find the first and 15^th term of the A.P.

Solution:  Let a be the first term and d be the common difference.

We know that, sum of first n terms is:

S_n = n/2(2a + (n – 1)d)

Also, nth term = a_n = a + (n – 1) d

According to the question,

S_q = 162

and  a₆ : a ₁₃ = 1 : 2

Now,  2a₆ = a₁₃

⇒ 2 [a + (6 – 1d)] = a + (13 – 1)d

⇒ 2a + 10d = a + 12d

⇒ a = 2d                                                                                 . . . . (1)

Also, S_9­ = 162

⇒  S₉ = 9/2(2a + (9 – 1)d)

⇒ 162 =  9/2(2a + 8d)

⇒ 162 X 2 = 9 [ 4d + 8d]                    [from (1)]

⇒ 324 = 9 X 12d

⇒ d = 3

⇒ a = 2d                                              [from (1)]

⇒ a = 6

Thus, the first term of the A.P. is 6

Now, a₁₅ = a + 14d = 6 + 14 X 3 = 6 + 42

a ₁₅ = 48

Therefore, 15^th term of the A.P. is 48

Question 29. If the 10^th term of an A.P. is 21 and the sum of its first 10 terms is 120, find its n^th term.

Solution:  Let a be the first term and d be the common difference.

We know that, sum of first n terms is :

S_n = n/2(2a + (n – 1)d)

and n^th term is given by:

a_n = a + (n – 1)d

Now,

given in question,

S₁₀ = 120

⇒  120 = 10/2(2a + (10 – 1)d)

⇒ 120 = 5 (2a + 9d)

⇒ 24 = 2a + 9d                                                                            . . . .(1)

Also,

a₁₀ = 21

⇒ 21 = a + (10 – 1)d

⇒ 21 = a + 9d                                                                              . . . . (2)

Subtracting (2) from (1), we get

24 – 21 = 2a + 9d – a – 9d

a = 3

Putting a = 3 in equation (2), we have

3 + 9d = 21

9d = 18

d = 2

So, we have now

first term = 3

common difference = 2

Therefore, the n^th term can be calculated by:

a_n = a + (n – 1)d

= 3 + (n – 1) 2

= 3 + 2n - 2

= 2n + 1

Therefore, the n^th term of the A.P is (a_n) = 2n + 1

Question 30. The sum of first 7 terms of an A.P. is 63 and the sum of its next 7 terms is 161. Find the 28^th term of this A.P.

Solution:  Let a be the first term and d be the common difference.

We know that, sum of first n terms

S_n = n/2(2a + (n – 1)d)

It is given that sum of the first 7 terms of an A.P. is 63.

And sum of next 7 terms is 161.

Sum of first 14 terms = Sum of first 7 terms + sum of next 7 terms

= 63 + 161 = 224

Now,    S₇ = 7/2(2a + (7 – 1)d)

⇒ 63 (2) = 7 (2a + 6d)

⇒ 9 X 2 = 2a + 6d

⇒ 2a + 6d = 18                                                           . . . . (1)

Also,    S₁₄ = 14/2(2a + (14 – 1)d)

⇒ 224 = 7 (2a + 13d)

⇒ 32 = 2a + 13d                                                         . . . . (2)

On subtracting (1) from (2), we get

⇒ 13d – 6d = 32 – 18

⇒ 7d = 14

⇒ d = 2

From (1)

2a + 6 (2) = 18

2a = 18 – 12

a = 3

Also, n^th term = a_n = a + (n – 1)d

⇒ a₂₈ = a + (28 – 1)d

= 3 + 27 (2)

= 3 + 54

= 57

Thus, the 28^th term is 57.

Question 31. The sum of first seven terms of an A.P. is 182. If its 4^th and 17^th terms are in ratio 1 : 5, find the A.P.

Solution:  In the given problem,

let us take the first term as a

and the common difference as d.

Here, we are given that,

S₁₇ = 182

We know that, sum of first term is:

S_n = n/2(2a + (n – 1)d)

So, from question

S₇ = 7/2(2a + (7 – 1)d)

182 X 2 = 7 (2a + 6d)

364 = 14a + 42d

26 = a + 3d

a = 26 – 3d                                                                                           . . . (1)

Also,

we are given that 4^th term and 17^th term are in a ratio 0f 1 : 5

Therefore,

⇒ 5 (a₄) = 1 (a₁₇)

⇒ 5 (a + 3d) = 1 (a + 16d)

⇒ 5a + 15d = a + 16d

⇒ 4a = d                                                                                             . . . . (2)

On substituting (2) in (1), we get

⇒ 4 (26 – 3d) = d

⇒ 104 – 12d = d

⇒ 104 = 13d

⇒ d = 8

from (2), we get

⇒ 4a = d

⇒ 4a = 8

⇒ a = 2

Thus we get, first term a = 2 and the common difference d = 8.

The required A.P. is 2, 10, 18, 26, . . .

Question 33. In an A.P. the sum of first ten terms is - 150 and the sum of its next 10 term is - 550. Find the A.P.

Solution:  Here, we are given S_n, = - 150 and sum of the next ten terms is - 550.

Let us take the first term of the A.P. as a

and the common difference as d.

So, let us first find S10.

For the sum of first 10 terms of this A.P,

First term = a

Last term = a₁₀

So, we know,

a_n = a + (n – 1)d

For the 10th term (n = 10),

a_n = a + (10 – 1)d

= a + 9d

So, here we can find the sum of the n terms of the given A.P., using the formula,

S_n = (n/2)(a + l)

Where, a = the first term

l = the last term

So, for the given A.P,

S₁₀ = (10/2)(a + a + 9d)

- 150 = 5 (2a + 9d)

- 150 = 10a + 45 d

a = (150 – 45d)/10                                           . . . . (1)

Similarly, for the sum of next 10 terms (S₁₀),

First term = a₁₁

Last term = a₂₀

For the 11^th term (n = 11),

a₁₁ = a + (11 – 1) d

= a + 10d

For the 20^th term (n = 20),

a₂₀ = a + (20 – 1) d

= a + 19d

So, for the given AP,

S₁₀ = (10/2)(a + 10d + a + 19d)

- 550 = 5 (2a + 29d)

- 550 = 10a + 145d

a = (−550 – 145d)/10                                           . . . . (2)

Now subtracting (1) from (2),

a – a =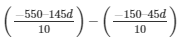

0 = - 550 – 145d + 150 + 45d

0 = - 400 – 100d

100d = – 400

d = - 4

Substituting the value of d in (1)

a =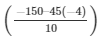

a =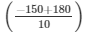 

= 3

So, the A.P. is 3, - 1, - 5, - 9,. . .  with a = 3, d = - 4

Question 35. In an A.P. , the first term is 2, the last term is 29 and the sum of the terms is 155, find the common difference of the A.P.

Solution:  In the given problem,

we have the first and the last term of an A.P. along with the sum of all the terms of A.P.

Here, we need to find the common difference of the A.P.

Here,

The first term of the A.P (a) = 2

The last term of the AP (l) = 29

Sum of all the terms (S_n) = 155

Let the common difference of the A.P. be d.

So, let us first find the number of the terms (n) using the formula,

155 = n/2(2 + 29)

155 (2) = n (31)

31n = 310

n = 10

Now, to find the common difference of the A.P. we use the following formula,

l = a + (n – 1) d

We get,

29 = 2 + (10 – 1)d

29 = 2 + (9)d

29 - 2 = 9d

9d = 27

d = 3

Therefore, the common difference of the A.P. is d = 3

Question 37. Find the number of terms of the A.P. - 12, - 9, - 6, . . . , 21. If 1 is added to each term of this A.P., then find the sum of all terms of the A.P. thus obtained.

Solution:  First term, a1 = - 12

Common difference, d = a2 – a1 = - 9 – (– 12)

= – 9 + 12 = 3

n^th term =         a_n = a + (n – 1)d

⇒ 21 = - 12 + (n – 1)3

⇒ 21 = - 12 + 3n – 3

⇒ 21 = 3n – 15

⇒ 36 = 3n

⇒   n = 12

Therefore, the number of terms is 12

Now, when 1 is added top each of the 12 terms, the sum will increase by 12.

So, the sum of all the terms of the A.P. thus obtained

⇒ S₁₂  + 12  = 12/2[a + l] + 12

= 6 [ - 12 + 21] + 12

= 6 X 9 + 12

= 66

Therefore, the sum after adding 1 to each of the term we get 66

Question 38. The sum of first n terms of an A.P. is 3n²  + 6n. Find the n^th term of this A.P.

Solution:  In  the given problem,

let us take the first term as a

and the common difference as d.

we know that n^th term is given by:

a_n = S_n   – S_{n - 1}

we have given here

S_n = 3n²  + 6n

So, using this to find the n^th term,

⇒ a_n = [3n²  + 6n] – [3(n – 1)²  + 6 (n – 1)]

= [3n²  + 6n] – [ 3 (n²  + 1²  – 6n) + 6n – 6]

= 3n²  + 6n – 3n²  – 3 + 6n – 6n + 6

= 6n + 3

Therefore, the n^th term of this A.P. is 6n + 3

Question 39. The sum of n terms of an A.P. is 5n – n². Find the n^th term of this A.P.

Solution:  Let a be the first term and d be the common difference.

We know that, sum of first n terms is :

S_n = n/2(2a + (n – 1)d)

It is given that sum of the first n terms of an A.P. is 5n – n².

First term = a = S₁ = 5 (1) – (1)² = 4.

Sum of first two terms = S₂ = 5 (2) – (2)² = 6.

Second term = S₂  – S₁ = 6 – 4 = 2.

Common difference = d = Second term – First term

= 2 – 4 = - 2

Also, nth term = a_n = a + (n – 1) d

⇒ a_n = 4 + (n – 1)( - 2)

⇒ a_n = 4 – 2n + 2

⇒ a_n = 6 – 2n

Thus, nth term of this A.P. is 6 – 2n.

Question 41. The sum of first n terms of an A.P. is 3n² + 4n. Find the 25^th term of this A.P.

Solution:  In the given problem,

we have sum of n terms as

S_n = 5n²  + 3n

we know,

a_n = S_n  – S_{n - 1}

We have to find out 25^th term, so n = 25

⇒ a₂₅ = S₂₅  – S₂₄

= [3 (25)²  + 4 (25)] – [ 3 (24)²  + 4 (24)]

= (3 X 625 + 100) – (3 X 576 + 96)

= 1975 – 1824

= 151

Therefore, its 25^th term is 151

Question 42. The sum of first n terms of an A.P. is 5n²  + 3n. If its m^th term is 168, find the value of m. Also find the 20^th term of this A.P.

Solution: Here, we are given the Sum of the A.P. as  S_n = 5n²  + 3n.

and its m^th term is a_m­ = 168

Let us assume its first term as a,

and the common difference as d

We know,

a_n = S_n  – S_{n - 1}

So, here

⇒ a_n = (5n²  + 3n) – [ 5(n – 1)²  + 3 (n – 1)]

= 5n²  + 3n – [ 5(n²  + 1 – 2n) + 3n – 3]

= 5n²  + 3n – 5n² - 5 + 10n – 3n + 3

= 10n – 2

We are given,

a_m = 168

Putting m in place of n , we get

⇒ a_m = 10m – 2

= > 168 = 10m – 2

⇒ 10m = 170

⇒ m = 17

and

a₂₀ = S₂₀  – S₁₉

= [5 (20)²  + 3 (20)] – [5 (19)²  + 3 (19)]

= [2000 + 60] – [1805 + 57]

= 2060 – 1862

= 198

Therefore, in the given A.P. m = 17 and the 20^th term is a₂₀  = 198

Question 45. If the sum of first n terms of an A.P. is 4n – n² , what is the first term? What is the sum of first two terms? What is the second term? Similarly find the third, the tenth and the n­^th term.

Solution:  In the given problem,

the sum of n terms of an A.P. is given by the expression, S„ = 4n – n²

So here, we can find the first term by substituting n = 1,

S„ = 4n – n²

= 4(1)—1²

= 4 – 1

= 3

Similarly, the sum of first two terms can be given by,

S₂ = 4(2) – (2)²

= 8 – 4

= 4

Now, as we know,

a_n = S_n  – S_{n - 1}

So,

a₂ = S₂  – S₁

= 4 – 3

= 1

Now, using the same method we have to find the third, tenth and nth term of the A.P.

So, for the third term,

a₃ = S₃  – S₂

= [4 (3) – (3)²] – [4(2) – (2)²]

= (12 – 9) – (8 – 4)

= 3 – 4

= - 1

Also, for the tenth term.

a₁₀   = S₁₀  – S₉

= [44(10) – (10)²]  – [4(9) – (9)²]

= (40 – 100) – (36 – 81)

= – 60 + 45

= - 15

So, for the nth term,

a_n = S_n  – S­_{n - 1}

= [4(n) – (12)²] – [4(n – 1) – (n – 1)²]

= (4n –  n²) – (4n – 4 – n²  – 1 + 2n)

= 4n – n² – 4n + 4 + n²  + 1 – 2n

= 5 – 2n

Therefore, a = 3, S₂ = 4, a₂ = 1, a₃ = - 1, a₁₀ = - 15