Ex-9.6 Arithmetic Progressions (Part - 4), Class 10, Maths RD Sharma Solutions | Extra Documents, Videos & Tests for Class 10 PDF Download
Question 46. If the sum of first n terms of an A.P. is 1/2(3n2 + 7n) , then find its nth term. Hence write the 20thterm.
Solution: Let a be the first term and d be the common difference.
We know that, sum of first n terms is:
Sn = n/2(2a + (n – 1)d)
It is given that the sum of the first n terms of an A.P. is:
1/2(3n2 + 7n)
Therefore, first term (a) = S1 = 1/2(3(1)2 + 7(1))
= 1/2(3X1 + 7)
= 1/2(10)
= 5
Sum of first two terms = S2 = 1/2(3(2)2 + 7(2))
= 1/2(3X4 + 14)
= 1/2(26)
= 13
Therefore, second term = S2 – S1
= 13 – 5 = 8
Common difference = d = second term – first term
= 8 – 5 = 3
Also, nth term of the A.P. is : a + (n – 1)d
= 5 + (n – 1)3
= 5 + 3n – 3
= 3n + 2
Thus, nth term of this A.P. is 3n + 2.
Now, we have to find the 20th term, so
Putting n = 2o in the above equation, we get
a20 = 3 (20) + 2
= 60 + 2
= 62
Thus, 20th term of this A.P. is 62.
Question 47. In an A.P. the sum of first n terms is 3n2/2 + (13/2).n. Find its 25th term.
Solution: Here the sum of first n terms is given by the expression,
Sn = 3n2/2 + (13/2).n
We need to find the 25th term of the A.P.
So, we know that the nth term of an A.P. is given by,
an = Sn – Sn-1
So, a25 = S25 – S24 . . . . (1)
So, using the expression for the sum of n terms,
we find the sum of 25 terms (S25) and the sum of 24 terms (S25), we get,
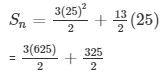
= 2200/2
= 1100
Similarly,
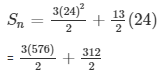
= 2040/2
= 1020
Now, using the above values in (1),
a21 = S25 – S24
= 1100 – 1020
= 80
Therefore, a25 = 80
Question 48. Find the sum of all natural numbers between 1 and 100, which are divisible by 3.
Solution: In this problem,
we need to find the sum of all the multiples of 3 lying between 1 and 100.
So, we know that the first multiple of 3 after 1 is 3
and the last multiple of 3 before 100 is 99.
Also, all these terms will form an A.P. with the common difference of 3.
So here,
First term (a) = 3
Last term (l) = 99
Common difference (d) = 3
So, here the first step is to find the total number of terms.
Let us take the number of terms as n.
Now, as we know,
an = a + (n – 1)d
So, for the last term,
99 = 3 + (n – 1)3
⇒ 99 = 3 + 3n – 3
⇒ 99 = 3n
Further simplifying,
⇒ n = 33
Now, using the formula for the sum of n terms,
i.e. Sn = n/2[2a + (n – 1)d]
we get,
⇒ S33 = 33/2[2(3) + (33 – 1)3]
= S33 = 33/2[6 + (32)3]
= S33 = 33/2[6 + 96]
= S33 = (33(102))/2
= 33 (51)
= 1683
Therefore, the sum of all the mulstiples of 3 lying between 1 and 100 is Sn = 1683
Question 50. Find the sum of all odd numbers between (i) 0 and 50 (ii) 100 and 200.
Solution:
(i) In this problem, we need to find the sum of all odd numbers lying between 0 and 50.
So, we know that the first odd number after 0 is 1
and the last odd number before 50 is 49.
Also, all these terms will form an AP. with the common difference of 2.
So here,
First term (a) = 1
Last term (0 = 49
Common difference (d) = 2
So, here the first step is to find the total number of terms.
Let us take the number of terms as n. Now, as we know,
an = a + (n -1)d
So, for the last term,
⇒ 49 = 1 + (n – 1)d
⇒ 49 = 1 + 2n – 2
⇒ 49 = 2n – 2
⇒ 49 + 1 = 2n
Further simplifying,
⇒ 50 = 2n
⇒ n = 25
Now, using the formula for the sum of n terms,
⇒ Sn = n/2[2a + (n – 1)d]
for n = 25, we get
⇒ S25 = 25/2[2(1) + (25 – 1)2]
= 25/2[2 + 24×2]
= 25 X 25
= 625
Therefore, the sum of all the odd numbers lying between 0 and 50 is 625.
(ii) In this problem,
we need to find the sum of all odd numbers lying between 100 and 200.
So, we know that the first odd number after 0 is 101
and the last odd number before 200 is 199.
Also, all these terms will form an AR. with the common difference of 2.
So here,
First term (a) = 101
Last term (an) = 199
Common difference (d) = 2
So, here the first step is to find the total number of term.
Let us take the number of terms as n.
Now, as we know,
an = a + (n – 1)d
So, for the last term,
⇒ 199 = 101 + (n – 1)2
⇒ 199 = 101 + 2n – 2
⇒ 199 = 99 + 2n
⇒ 199 – 99 = 2n
Further simplifying,
⇒ 100 = 2n
⇒ n = 50
Now, using the formula for the sum of n terms,
Sn = n/2[2(a) + (n – 1)d]
For n = 50, we get
⇒ S50 = 50/2[2(101) + (50 – 1)2]
= 25 [ 202 + (49) 2 ]
= 25(202 + 98)
= 25 (300)
= 7500
Therefore, the sum of all the odd numbers lying between 100 and 200 is 7500
Question 52. Find the sum of all integers between 84 and 719, which are multiples of 5.
Solution: In this problem,
we need to find the sum of all the multiples of 5 lying between 84 and 719.
So, we know that the first multiple of 5 after 84 is 85
and the last multiple of 5 before 719 is 715.
Also, all these terms will form an A.P.
with the common difference of 5.
So here,
First term (a) = 85
Last term (l) = 715
Common difference (d) = 5
So, here the first step is to find the total number of terms.
Let us take the number of terms as n.
Now, as we know,
a = a + (n -1)d
So, for the last term.
715 = 85 + (n – 1)5
715 = 85 + 5n – 5
715 = 80 + 5n
715 – 80 = 5n
Further simplifying,
635 = 5n
n = 127
Now, using the formula for the sum of n terms,
Sn = n/2[2a + (n – 1)d]
For n = 127,
S127 = 127/2[2(85) + (127 – 1)5]
= 127/2[170 + 630]
= (127(800))/2
= 50800
Therefore, the sum of all the multiples of 5 lying between 84 and 719 is 50800.
Question 53. Find the sum of all integer between 50 and 500, which are divisible by 7.
Solution: In this problem,
we need to find the sum of all the multiples of 7 lying between 50 and 500.
So, we know that the first multiple of 7 after 50 is 56
and the last multiple of 7 before 500 is 497.
Also, all these terms will form an A.P. with the common difference of 7.
So here,
First term (a) = 56
Last term (l) = 497
Common difference (d) = 7
So, here the first step is to find the total number of terms.
Let us take the number of terms as n.
Now, as we know,
an = a + (n – 1)d
So, for the last term.
497 = 56 + (n – 1)7
⇒ 497 = 56 + 7n -7
⇒ 497 = 49 + 7n
⇒ 497 – 49 = 7n
Further simplifying,
448 = 7n
n = 64
Now, using the formula for the sum of n terms,
Sn = n/2[2a + (n – 1)d]
for n = 64, we get
S64 = 64/2[2(56) + (64 – 1)7]
= 32 [ 112 + (63)7]
= 32 [112 + 441]
= 32 (553)
= 17696
Therefore, the sum of all the multiples of 7 lying between 50 and 500 is 17696
Question 54. Find the sum of all even integers between 101 and 999.
Solution: In this problem,
we need to find the sum of all the even numbers lying between 101 and 999.
So, we know that the first even number after 101 is 102
and the last even number before 999 is 998.
Also, all these terms will form an A.P. with the common difference of 2.
So here,
First term (a) = 102
Last term (l) = 998
Common difference (d) = 2
So, here the first step is to find the total number of terms.
Let us take the number of terms as n.
Now, as we know,
an = a + (n – 1)d
So, for the last term,
⇒ 998 = 102 + (n – 1)2
⇒ 998 = 102 + 2n – 2
⇒ 998 = 100 + 2n
⇒ 998 – 100 = 2n
Further simplifying,
⇒ 898 = 2n
⇒ n = 449
Now, using the formula for the sum of n terms,
Sn = n/2[2a + (n – 1)d]
For n = 449, we get
S449 = 449/2[2(102) + (449 – 1)2]
= 449/2[204 + (448)2]
= 449/2[204 + 896]
= 449/2[1100]
= 449 (550)
= 246950
Therefore, the sum of all even numbers lying between 101 and 999 is 246950
Question 55.
(i) Find the sum of all integers between 100 and 550, which are divisible by 9.
Solution: In this problem,
we need to find the sum of all the multiples of 9 lying between 100 and 550.
So, we know that the first multiple of 9 after 100 is 108
and the last multiple of 9 before 550 is 549.
Also, all these terms will form an A.P. with the common difference of 9.
So here,
First term (a) = 108
Last term (l) = 549
Common difference (d) = 9
So, here the first step is to find the total number of terms.
Let us take the number of terms as n.
Now, as we know,
an = a + (n – 1)d
So, for the last term.
⇒ 549 = 108 + (n – 1)d
⇒ 549 = 108 + 9n – 9
⇒ 549 = 99 + 9n
⇒ 549 – 99 = 9n
Further simplifying
⇒ 9n = 450
⇒ n = 50
Now, using the formula for the sum of n terms,
Sn = n/2[2a + (n – 1)d]
We get,
Sn = 50/2[2(108) + (50 – 1)9]
= 25 [ 216 + (49)9 ]
= 25 (216 + 441)
= 25 (657)
= 16425
Therefore, the sum of all the multiples of 9 lying between 100 and 550 is 16425
Question 56. Let there be an A.P. with first term ‘a’, common difference ‘d’. If an denotes its nth term and Sn the sum of first n terms, find.
(i) n and Sn, if a = 5 , d = 3 , and an = 50.
(ii) n and a, if an = 4 , d = 2 and Sn = -14.
(iii) d, if a = 3, n = 8 and Sn = 192.
(iv) a, if an = 28, Sn = 144 and n = 9.
(v) n and d, if a = 8, an = 62 and Sn = 120.
(vi) n and an , if a = 2, d = 8 and Sn = 90.
Solution:
(i) Here, we have an A.P. whose nth term (an), first term (a) and common difference (d) are given. We need to find the number of terms (n) and the sum of first n terms (Sn).
Here,
First term (a) = 5
Last term (an) = 50
Common difference (d) = 3
So here we will find the value of n using the formula, an = a + (n – 1) d
So, substituting the values in the above mentioned formula
⇒ 50 = 5 + (n – 1) 3
⇒ 50 = 5 + 3n – 3
⇒ 50 = 2 + 3n
⇒ 3n = 50 – 2
Further simplifying for n,
3n = 48
n = 16
Now, here we can find the sum of the n terms of the given A.P., using the formula,
Sn = (n/2)(a + l)
Where, a = the first term
l = the last term
So, for the given A.P,
on substituting the values in the formula for the sum of n terms of an A.P., we get,
S16 = (16/2)(5 + 50)
= 8 (55)
= 440
Therefore, for the given A.P. we have, n = 16 and S16 = 440
(ii) Here, we have an A.P. whose nth term (an), sum of first n terms (S0) and common difference (d) are given. We need to find the number of terms (n) and the first term (a).
Here,
Last term (l) = 4
Common difference (d) = 2
Sum of n terms (Sn) = -14
So here we will find the value of n using the formula, an = a + (n -1) d
So, substituting the values in the above mentioned formula
⇒ 4 = a + (n – 1) 2
⇒ 4 = a + 2n - 2
⇒ 4 + 2 = a + 2n
⇒ n = (6 – a)/2 . . . . (1)
Now, here the sum of the n terms is given by the formula,
Sn = (n/2)(a + l)
Where, a = the first term
l = the last term
So, for the given A.P,
on substituting the values in the formula for the sum of n terms of an A.P., we get,
⇒ −14 = n/2(a + 4)
⇒ 14 (2) = n (a + 4)
⇒ n = −28/(a + 4) . . . . (2)
Equating (1) and (2), we get,
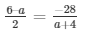
(6 – a)(a + 4) = -28(2)
6a – a2 + 24 – 4a = -56
-a2 + 2a + 24 + 56 = 0
So, we get the following quadratic equation,
-a 2 + 2a + 80 = 0
a2 – 2a – 80 = 0
Further solving it for a by splitting the middle term,
a2 – 2a – 80 = 0
a2 – 10a + 8a – 80 = 0
a(a – 10) + 8(a – 10) = 0
(a – 10)(a + 8) = 0
So, we get,
a – 10 = 0
a = 10
or,
a + 8 = 10
a = -8
Substituting, a = 10 in (1)
n = (6 – 10)/2
n = −4/2
n = -2
Here, we get n as negative, which is not possible. SO, we take a = -8
n = (6 – (−8))/2
n = (6 + 8)/2
n = 14/2
n = 7
Therefore, for the given A.P. n = 7 and a = -8
(iii) Here, we have an A.P. whose first term (a), sum of first n terms (S0) and the number of terms (n) are given. We need to find common difference (d).
Here,
First term (a) = 3
Sum of n terms (Sn) = 192
Number of terms (n) = 8
So here we will find the value of n using the formula, an = a + (n -1) d
So, to find the common difference of this A.P.,
we use the following formula for the sum of n terms of an A.P
Sn = (n/2)[2a + (n – 1)d]
Where; a = first term for the given A.P.
d = common difference of the given A.P.
n = number of terms
So, using the formula for n = 8, we get,
S8 = (8/2)[2(3) + (8 – 1)d]
192 = 4 [ 6 + 7d ]
192 = 24 + 28d
28d = 192 – 24
28d = 168
d = 6
Therefore, the common difference of the given A.P. is d = 6
(iv) Here, we have an A.P. whose nth term (an), sum of first n terms (Sn) and the number of terms (n) are given. We need to find first term (a).
Here,
Last term (a9) = 28
Sum of n terms (Sn) = 144
Number of terms (n) = 9
Now,
a9 = a + 8d
28 = a + 8d . . . . (1)
Also, using the following formula for the sum of n terms of an AP
Sn = (n/2)[2a + (n – 1)d]
Where; a = first term for the given A.P.
d = common difference of the given A.P.
n = number of terms
So, using the formula for n = 9, we get,
S9 = (9/2)[2a + (9 – 1)d]
144 (2) = 9 [2a + 8d]
288 = 18a + 72d . . . . (2)
Multiplying (1) by 9, we get
9a + 72d = 252 . . . . (3)
Further, subtracting (3) from (2), we get
9 a = 36
a = 4
Therefore, the first term of the given A.P. is a = 4
(v) Here, we have an A.P. whose nth term (an), sum of first n terms (Sn) and first term (a) are given. We need to find the number of terms (n) and the common difference (d).
Here,
First term (a) = 8
Last term (an ) = 62
Sum of n terms (Sn) = 210
Now, here the sum of the n terms is given by the formula,
Sn = (n/2)(a + l)
Where, a = the first term
l = the last term
So, for the given A.P,
on substituting the values in the formula for the sum of n terms of an A.P., we get,
210 = n/2[8 + 62]
210 (2) = n (70)
n = 420/70
n = 7
Also, here we will find the value of d using the formula,
an = a + (n – 1) d
So, substituting the values in the above mentioned formula
62 = 8 + (6 – 1)d
5d = 54
d = 54/5
Therefore, for the given A.P. n = 6 and d = 54/5
(vi) Here, we have an A.P. whose first term (a), common difference (d) and sum of first n terms are given. We need to find the number of terms (n) and the nth term (an).
Here,
First term (a) = 2
Sum of first nth terms (Sn) = 90
Common difference (d) = 8
So, to find the number of terms (n) of this A.P.,
we use the following formula for the sum of n terms of an A.P
Sn = (n/2)[2a + (n – 1)d]
Where; a = first term for the given A.P.
d = common difference of the given A.P.
n = number of terms
So, using the formula for d = 8, we get,
Sn = (n/2)[2(2) + (n – 1)8]
90 = (n/2)[4 + 8n – 8]
90 (2) = n [ 8n – 4 ]
180 = 8n2 – 4n
Further solving the above quadratic equation,
8n2 -4n -180 = 0
2n2 – n – 45 = 0
Further solving for n,
2n2 – 10n + 9n – 45 = 0
2n(n – 5) + 9(n – 5) = 0
(2n – 9)(n – 5) = 0
Now,
2n + 9 = 0
n = −9/2
Also,
n – 5 = 0
n = 5
Since, n cannot be a fraction.
Thus, n = 5
Also, we will find the value of nth term (an), using the formula,
an = a + (n – 1) d
So, substituting the values in the above formula,
an = 2 + (5 – 1) 8
an = 2 + 4 (8)
an = 2 + 32
an = 34
Therefore, for the given A.P., n = 5 and an = 34
|
5 videos|292 docs|59 tests
|
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















