Coordinate Geometry Exercise 14.1 (Part-7) | Extra Documents, Videos & Tests for Class 10 PDF Download
Question 21: Find the ratio in which the point P(−1, y) lying on the line segment joining A(−3, 10) and B(6 −8) divides it. Also find the value of y.
Answer : Suppose P(−1, y) divides the line segment joining A(−3, 10) and B(6 −8) in the ratio k : 1.
Using section formula, we get
Coordinates of P = 
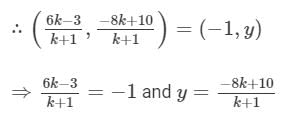
Now
, 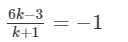
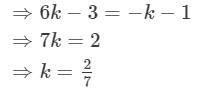
So, P divides the line segment AB in the ratio 2 : 7.
Putting k = 2/7 in Y = 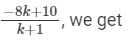

Hence, the value of y is 6.
Question 22: Find the coordinates of a point A, where AB is a diameter of the circle whose centre is (2, −3) and Bis (1, 4).
Answer :
Let the co-ordinates of point A be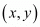 .
.
Centre lies on the mid-point of the diameter. So applying the mid-point formula we get,

x = 3
Similarly,
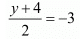
y = -10
So the co-ordinates of A are (3,−10)
Question 23: If the points (−2, −1), (1, 0), (x, 3) and (1, y) form a parallelogram, find the values of x and y.
Answer :
Let ABCD be a parallelogram in which the co-ordinates of the vertices are A (−2,−1); B (1, 0); C (x, 3) and D (1, y).
Since ABCD is a parallelogram, the diagonals bisect each other. Therefore the mid-point of the diagonals of the parallelogram will coincide.
In general to find the mid-point of two points
of two points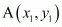 and
and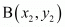 we use section formula as,
we use section formula as,
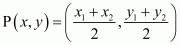
The mid-point of the diagonals of the parallelogram will coincide.
So,
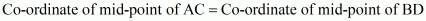
Therefore,
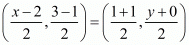
Now equate the individual terms to get the unknown value. So,
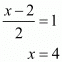
Similarly,
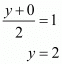
Therefore,

Question 24: The points A(2, 0), B(9, 1) C(11, 6) and D(4, 4) are the vertices of a quadrilateral ABCD. Determine whether ABCD is a rhombus or not.
Answer :
Let A (2, 0); B (9, 1); C (11, 6) and D (4, 4) be the vertices of a quadrilateral. We have to check if the quadrilateral ABCD is a rhombus or not.
So we should find the lengths of sides of quadrilateral ABCD.
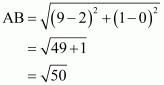
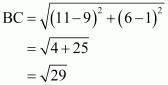
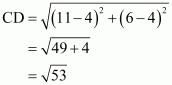

All the sides of quadrilateral are unequal. Hence ABCD is not a rhombus.
Question 25: In what ratio does the point (−4, 6) divide the line segment joining the points A(−6, 10) and B(3,−8)?
Answer :
The co-ordinates of a point which divided two points 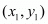 and
and 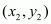 internally in the ratio
internally in the ratio 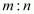 is given by the formula,
is given by the formula,
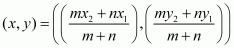
Here it is said that the point (−4,6) divides the points A(−6,10) and B(3,−8). Substituting these values in the above formula we have,
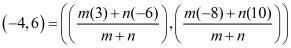
Equating the individual components we have,
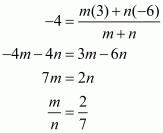
Therefore the ratio in which the line is divided is 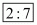
Question 26: Find the ratio in which the y-axis divides the line segment joining the points (5, −6) and (−1,−4). Also, find the coordinates of the point of division.
Answer :
The ratio in which the y-axis divides two points 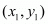 and
and 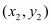 is λ:1
is λ:1
The co-ordinates of the point dividing two points 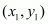 and
and 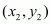 in the ratio
in the ratio 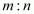 is given as,
is given as,
 where,
where, 
Here the two given points are A(5,−6) and B(−1,−4).
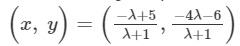
Since, the y-axis divided the given line, so the x coordinate will be 0.
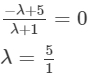
Thus the given points are divided by the y-axis in the ratio .
.
The co-ordinates of this point (x, y) can be found by using the earlier mentioned formula.
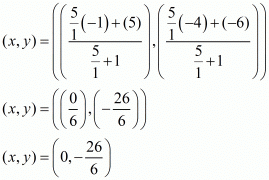
Thus the co-ordinates of the point which divides the given points in the required ratio are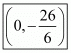 .
.
Question 27: Show that A (−3, 2), B (−5, −5), C (2,−3), and D (4, 4) are the vertices of a rhombus.
Answer :
Let A (−3, 2); B (−5,−5); C (2,−3) and D (4, 4) be the vertices of a quadrilateral. We have to prove that the quadrilateral ABCD is a rhombus.
So we should find the lengths of sides of quadrilateral ABCD.
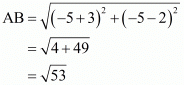
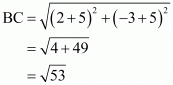
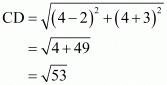
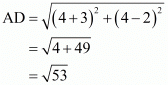
All the sides of quadrilateral are equal. Hence ABCD is a rhombus.
Question 28: Find the length of the medians of a ΔABC having vertices at A(0, −1), B(2, 1) and C(0, 3).
Answer :
We have to find the lengths of the medians of a triangle whose co-ordinates of the vertices are A (0,−1); B (2, 1) and C (0, 3).
So we should find the mid-points of the sides of the triangle.
In general to find the mid-point of two points
of two points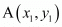 and
and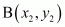 we use section formula as,
we use section formula as,
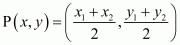
Therefore mid-point P of side AB can be written as,
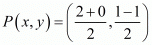
Now equate the individual terms to get,
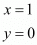
So co-ordinates of P is (1, 0)
Similarly mid-point Q of side BC can be written as,
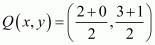
Now equate the individual terms to get,
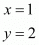
So co-ordinates of Q is (1, 2)
Similarly mid-point R of side AC can be written as,
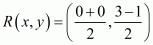
Now equate the individual terms to get,
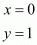
So co-ordinates of R is (0, 1)
Therefore length of median from A to the side BC is,
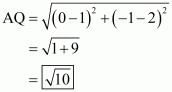
Similarly length of median from B to the side AC is,
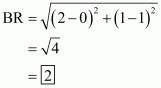
Similarly length of median from C to the side AB is

Question 29: Find the lengths of the medians of a ΔABC having vertices at A(5, 1), B(1, 5), and C(−3, −1).
Answer :
We have to find the lengths of the medians of a triangle whose co-ordinates of the vertices are A (5, 1); B (1, 5) and C (−3,−1).
So we should find the mid-points of the sides of the triangle.
In general to find the mid-point of two points
of two points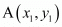 and
and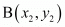 we use section formula as,
we use section formula as,
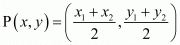
Therefore mid-point P of side AB can be written as,
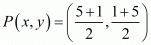
Now equate the individual terms to get,
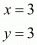
So co-ordinates of P is (3, 3)
Similarly mid-point Q of side BC can be written as,
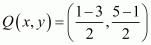
Now equate the individual terms to get,
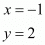
So co-ordinates of Q is (−1, 2)
Similarly mid-point R of side AC can be written as,
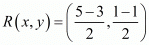
Now equate the individual terms to get,
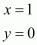
So co-ordinates of R is (1, 0)
Therefore length of median from A to the side BC is,
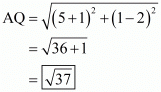
Similarly length of median from B to the side AC is,
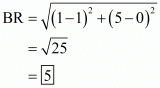
Similarly length of median from C to the side AB is

|
5 videos|292 docs|59 tests
|
|
5 videos|292 docs|59 tests
|

|
Explore Courses for Class 10 exam
|

|
















